Hcf Of 330 And 385
elan
Sep 11, 2025 · 6 min read
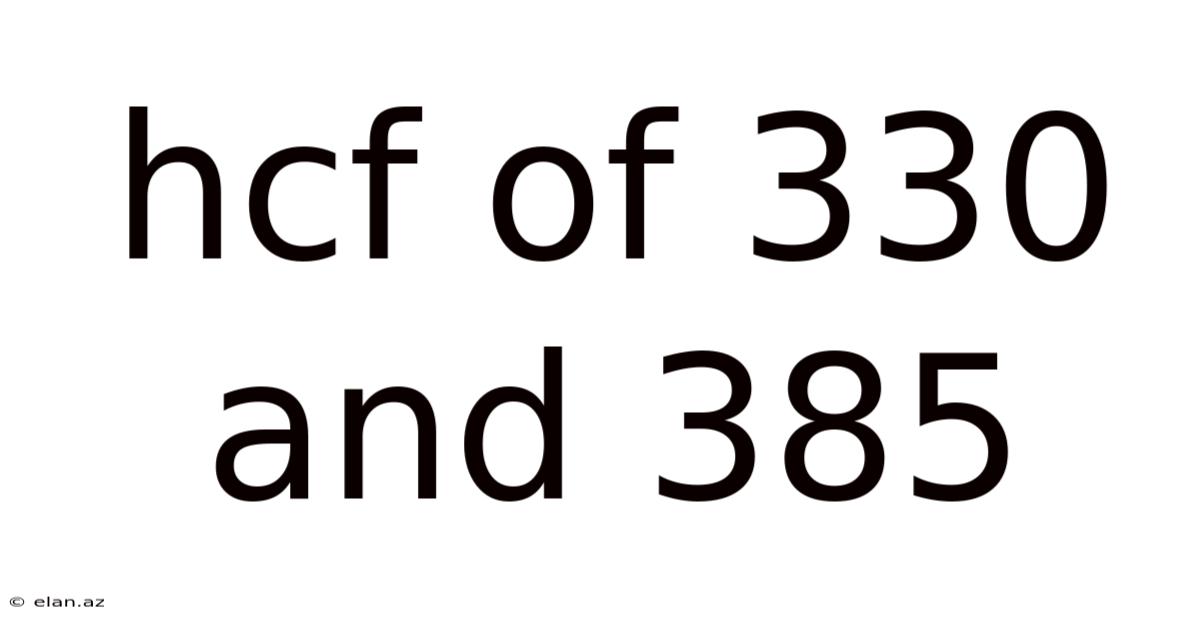
Table of Contents
Finding the Highest Common Factor (HCF) of 330 and 385: A Comprehensive Guide
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will guide you through several methods to determine the HCF of 330 and 385, explaining the underlying principles and providing a deeper understanding of this important mathematical operation. We'll cover prime factorization, the Euclidean algorithm, and explore the practical applications of finding the HCF.
Introduction to HCF and its Significance
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. Understanding HCF is crucial in various mathematical contexts, including simplifying fractions, solving problems involving ratios and proportions, and even in more advanced areas like abstract algebra. In this article, we’ll focus on finding the HCF of 330 and 385, using different approaches to illustrate the versatility of the concept.
Method 1: Prime Factorization
Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This method is particularly intuitive for smaller numbers.
Steps:
-
Find the prime factorization of 330:
- 330 = 2 × 165
- 165 = 3 × 55
- 55 = 5 × 11 Therefore, the prime factorization of 330 is 2 × 3 × 5 × 11.
-
Find the prime factorization of 385:
- 385 = 5 × 77
- 77 = 7 × 11 Therefore, the prime factorization of 385 is 5 × 7 × 11.
-
Identify common prime factors: Both 330 and 385 share the prime factors 5 and 11.
-
Calculate the HCF: Multiply the common prime factors together. In this case, the HCF is 5 × 11 = 55.
Therefore, the HCF of 330 and 385 using prime factorization is 55.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, especially useful for larger numbers where prime factorization becomes more complex. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which is the HCF.
Steps:
-
Start with the larger number (385) and the smaller number (330).
-
Divide the larger number by the smaller number and find the remainder:
- 385 ÷ 330 = 1 with a remainder of 55.
-
Replace the larger number with the smaller number (330) and the smaller number with the remainder (55).
-
Repeat the division process:
- 330 ÷ 55 = 6 with a remainder of 0.
-
Since the remainder is 0, the HCF is the last non-zero remainder, which is 55.
Therefore, the HCF of 330 and 385 using the Euclidean algorithm is 55.
Method 3: Listing Factors
This method is suitable for smaller numbers and involves listing all the factors of each number and identifying the largest common factor. While less efficient than prime factorization or the Euclidean algorithm for larger numbers, it’s a good method for building an intuitive understanding of HCF.
Steps:
-
List all the factors of 330: 1, 2, 3, 5, 6, 10, 11, 15, 22, 30, 33, 55, 66, 110, 165, 330
-
List all the factors of 385: 1, 5, 7, 11, 35, 55, 77, 385
-
Compare the lists and identify the common factors: 1, 5, 11, 55
-
The largest common factor is the HCF: The largest common factor is 55.
Comparison of Methods
All three methods – prime factorization, the Euclidean algorithm, and listing factors – correctly identify the HCF of 330 and 385 as 55. However, each method has its strengths and weaknesses:
-
Prime factorization: Intuitive for smaller numbers but can become cumbersome for larger numbers with many prime factors.
-
Euclidean algorithm: Highly efficient and works well for both small and large numbers. It’s generally the preferred method for larger numbers due to its speed and simplicity.
-
Listing factors: Simple to understand but inefficient for larger numbers as the number of factors increases dramatically.
Understanding the Result: What does HCF of 55 Mean?
The HCF of 330 and 385 being 55 means that 55 is the largest number that divides both 330 and 385 without leaving a remainder. This has practical implications:
-
Simplifying fractions: If you had a fraction like 330/385, you could simplify it by dividing both the numerator and denominator by their HCF (55), resulting in the simplified fraction 6/7.
-
Problem-solving: In problems involving quantities that need to be divided into equal groups, the HCF helps determine the largest possible size of those groups. For example, if you have 330 apples and 385 oranges, and you want to divide them into equal groups of the same size, the largest possible group size would be 55 (with 6 groups of apples and 7 groups of oranges).
Applications of HCF in Real-World Scenarios
The concept of HCF isn't confined to the classroom; it has various real-world applications:
-
Measurement and Cutting: Imagine you have two pieces of wood, one measuring 330 cm and the other 385 cm. You want to cut them into smaller pieces of equal length, without any waste. The HCF (55 cm) will tell you the largest possible length of each piece.
-
Resource Allocation: Imagine you're organizing a school trip. You have 330 students and 385 chaperones. You need to divide them into groups of equal size for activities. The HCF will help you determine the largest group size possible.
-
Scheduling: If two events repeat at intervals of 330 days and 385 days respectively, the HCF will help to determine when they will occur simultaneously again.
Frequently Asked Questions (FAQ)
-
What if the HCF of two numbers is 1? If the HCF of two numbers is 1, they are said to be relatively prime or coprime. This means they share no common factors other than 1.
-
Can the HCF of two numbers be larger than the smaller number? No. The HCF is always less than or equal to the smaller of the two numbers.
-
Are there other methods to find the HCF? Yes, there are more advanced methods for finding the HCF, particularly for very large numbers, that leverage concepts from number theory and computational algebra.
Conclusion
Finding the Highest Common Factor is a fundamental skill in mathematics with broad applications. We explored three different methods – prime factorization, the Euclidean algorithm, and listing factors – to determine the HCF of 330 and 385, which is 55. The Euclidean algorithm generally proves to be the most efficient method, especially for larger numbers. Understanding the HCF isn't just about solving mathematical problems; it's about developing logical reasoning and problem-solving skills applicable to various real-world situations. Remember that the key is to choose the method that best suits the numbers involved and your comfort level with different mathematical techniques. The ability to calculate the HCF efficiently is a valuable asset in both academic and practical settings.
Latest Posts
Latest Posts
-
7 4 As A Percent
Sep 11, 2025
-
Qi Words That Start With
Sep 11, 2025
-
A Colour Starting With A
Sep 11, 2025
-
5 Letter Words In French
Sep 11, 2025
-
What Is 25cl In Ml
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 330 And 385 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.