Hcf Of 375 And 150
elan
Sep 13, 2025 · 6 min read
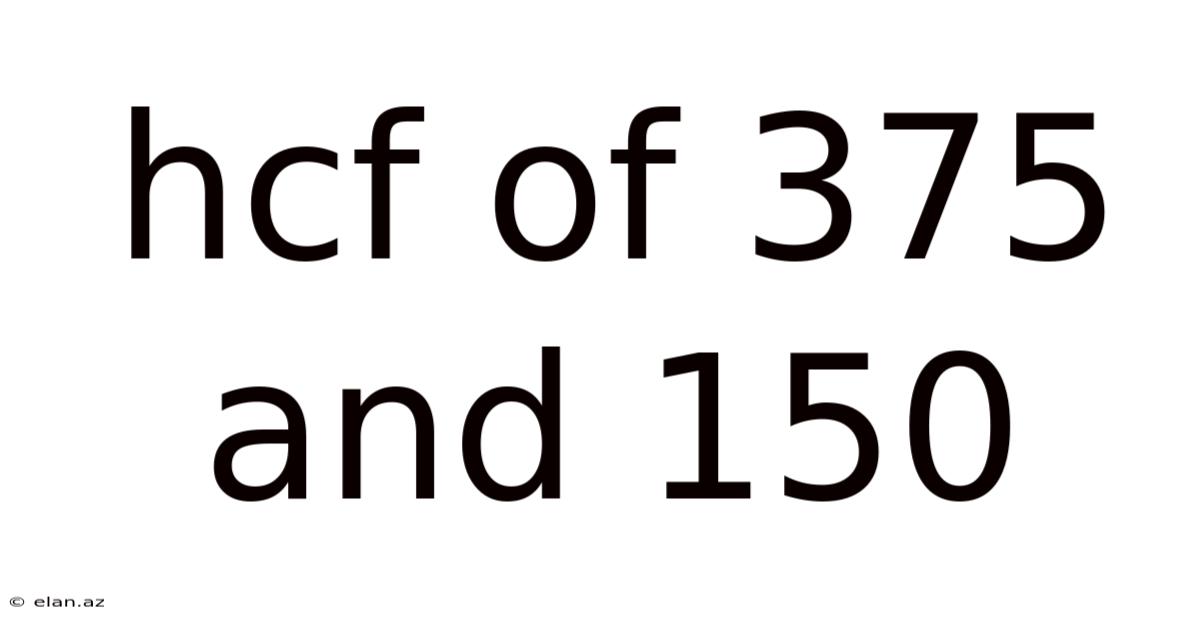
Table of Contents
Finding the Highest Common Factor (HCF) of 375 and 150: A Comprehensive Guide
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving complex algebraic equations. This article will delve into the various methods of calculating the HCF of 375 and 150, explaining the underlying principles and providing a deeper understanding of this crucial mathematical concept. We will explore prime factorization, the Euclidean algorithm, and even consider the visual representation of the HCF using Venn diagrams. By the end, you'll not only know the HCF of 375 and 150 but also possess a comprehensive toolkit for finding the HCF of any two numbers.
Understanding the Highest Common Factor (HCF)
The HCF of two or more numbers is the largest number that divides each of them without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The largest of these common factors is 6, therefore, the HCF of 12 and 18 is 6. Understanding this basic principle is crucial before we tackle the HCF of 375 and 150.
Method 1: Prime Factorization
Prime factorization is a powerful technique to find the HCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Steps:
-
Find the prime factorization of 375:
375 = 3 × 125 = 3 × 5 × 25 = 3 × 5 × 5 × 5 = 3 × 5³
-
Find the prime factorization of 150:
150 = 2 × 75 = 2 × 3 × 25 = 2 × 3 × 5 × 5 = 2 × 3 × 5²
-
Identify common prime factors: Both 375 and 150 share the prime factors 3 and 5.
-
Find the lowest power of common prime factors: The lowest power of 3 is 3¹ (or simply 3) and the lowest power of 5 is 5².
-
Multiply the lowest powers of common prime factors: HCF(375, 150) = 3 × 5² = 3 × 25 = 75
Therefore, the HCF of 375 and 150 is 75.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the HCF, particularly useful for larger numbers. It relies on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Steps:
-
Divide the larger number (375) by the smaller number (150): 375 ÷ 150 = 2 with a remainder of 75.
-
Replace the larger number with the remainder: Now we find the HCF of 150 and 75.
-
Repeat the division: 150 ÷ 75 = 2 with a remainder of 0.
-
The last non-zero remainder is the HCF: Since the remainder is 0, the HCF is the previous divisor, which is 75.
Therefore, the HCF of 375 and 150 using the Euclidean algorithm is 75. This method is particularly efficient for larger numbers as it avoids the need for complete prime factorization.
Method 3: Listing Factors
While less efficient for larger numbers, listing factors can be a helpful method for smaller numbers like these.
Steps:
-
List the factors of 375: 1, 3, 5, 15, 25, 75, 125, 375
-
List the factors of 150: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
-
Identify the common factors: The common factors are 1, 3, 5, 15, 25, and 75.
-
Determine the highest common factor: The highest common factor among these is 75.
Visual Representation: Venn Diagrams
While not a direct calculation method, Venn diagrams can visually represent the common factors and help understand the concept of the HCF. You would create two overlapping circles, one for the factors of 375 and one for the factors of 150. The overlapping section would represent the common factors. The largest number in the overlapping section would be the HCF. This method is primarily useful for illustrating the concept rather than for practical calculation, especially with larger numbers.
Why is finding the HCF important?
The HCF has several practical applications:
-
Simplifying fractions: Finding the HCF of the numerator and denominator allows you to simplify a fraction to its lowest terms. For example, the fraction 375/150 can be simplified to 5/2 by dividing both the numerator and denominator by their HCF, which is 75.
-
Solving word problems: Many word problems involving division or sharing require finding the HCF to determine the largest possible equal groups or portions.
-
Algebraic expressions: Finding the HCF is crucial in simplifying algebraic expressions by factoring out common terms.
-
Number theory: The HCF plays a vital role in various number theory concepts, such as modular arithmetic and cryptography.
Frequently Asked Questions (FAQ)
-
What is the difference between HCF and LCM? The Highest Common Factor (HCF) is the largest number that divides both numbers without a remainder, while the Least Common Multiple (LCM) is the smallest number that is a multiple of both numbers. They are related by the formula: HCF(a, b) × LCM(a, b) = a × b
-
Can the HCF of two numbers be 1? Yes, if two numbers are relatively prime (or coprime), meaning they share no common factors other than 1, then their HCF is 1.
-
Is there a limit to the size of numbers for which the HCF can be found? No, the methods described, particularly the Euclidean algorithm, can be used to find the HCF of arbitrarily large numbers. Computational limitations might arise with extremely large numbers, but the algorithms themselves are not restricted.
-
Why are prime factors important in finding the HCF? Prime factorization provides a fundamental building block representation of a number. By identifying the common prime factors and their lowest powers, we can directly construct the HCF.
Conclusion
Finding the HCF of 375 and 150, as demonstrated, can be achieved through various methods: prime factorization, the Euclidean algorithm, and listing factors. Each method offers a different approach, with the Euclidean algorithm being particularly efficient for larger numbers. Understanding these methods provides not just a solution to a specific problem but a deeper comprehension of fundamental mathematical concepts. The HCF is a building block for more advanced mathematical concepts, highlighting its importance across various mathematical fields and applications in everyday problem-solving. The ability to confidently calculate the HCF equips you with a valuable skill applicable beyond the classroom. Remember, the key is not just to find the answer (which is 75 in this case), but to grasp the underlying principles and methods that enable you to solve similar problems independently.
Latest Posts
Latest Posts
-
Convert 48 Cm To Inches
Sep 13, 2025
-
Fractions And Decimals To Percents
Sep 13, 2025
-
Fossil Fuels Benefits And Drawbacks
Sep 13, 2025
-
Hard Maths Questions With Answers
Sep 13, 2025
-
A Whole Number Crossword Clue
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 375 And 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.