Hcf Of 42 And 105
elan
Sep 23, 2025 · 6 min read
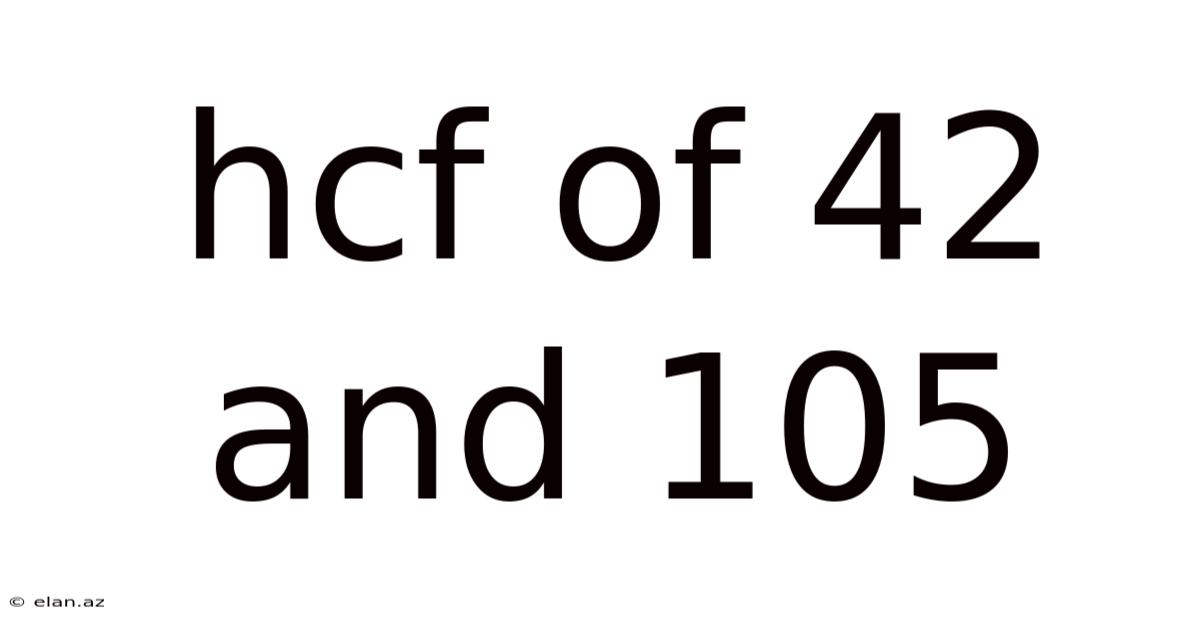
Table of Contents
Finding the Highest Common Factor (HCF) of 42 and 105: A Comprehensive Guide
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving more complex algebraic problems. This article provides a detailed explanation of how to find the HCF of 42 and 105, exploring various methods and delving into the underlying mathematical principles. Understanding this seemingly simple calculation opens doors to a deeper appreciation of number theory.
Introduction: What is the Highest Common Factor (HCF)?
The HCF of two or more numbers is the largest number that divides evenly into each of them without leaving a remainder. For example, the HCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Finding the HCF is crucial in simplifying fractions, solving equations, and understanding the relationships between numbers. This article focuses specifically on finding the HCF of 42 and 105, illustrating several different approaches.
Method 1: Prime Factorization
This method is considered a robust and fundamental approach to finding the HCF. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
1. Prime Factorization of 42:
42 can be broken down as follows:
- 42 = 2 x 21
- 21 = 3 x 7
Therefore, the prime factorization of 42 is 2 x 3 x 7.
2. Prime Factorization of 105:
105 can be broken down as follows:
- 105 = 3 x 35
- 35 = 5 x 7
Therefore, the prime factorization of 105 is 3 x 5 x 7.
3. Identifying Common Factors:
Now, we compare the prime factorizations of 42 and 105:
42 = 2 x 3 x 7 105 = 3 x 5 x 7
The common prime factors are 3 and 7.
4. Calculating the HCF:
To find the HCF, we multiply the common prime factors together:
HCF(42, 105) = 3 x 7 = 21
Therefore, the highest common factor of 42 and 105 is 21. This means that 21 is the largest number that divides both 42 and 105 without leaving a remainder.
Method 2: Listing Factors
This method is straightforward, especially for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
1. Factors of 42:
The factors of 42 are 1, 2, 3, 6, 7, 14, 21, and 42.
2. Factors of 105:
The factors of 105 are 1, 3, 5, 7, 15, 21, 35, and 105.
3. Identifying Common Factors:
Comparing the lists, we find the common factors are 1, 3, 7, and 21.
4. Determining the HCF:
The largest common factor is 21. Therefore, the HCF of 42 and 105 is 21. This method is less efficient for larger numbers but provides a clear visualization of the factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Steps:
- Divide the larger number (105) by the smaller number (42):
105 ÷ 42 = 2 with a remainder of 21.
- Replace the larger number with the remainder:
Now we find the HCF of 42 and 21.
- Repeat the division:
42 ÷ 21 = 2 with a remainder of 0.
- The HCF is the last non-zero remainder:
Since the remainder is 0, the HCF is the previous remainder, which is 21.
Therefore, the HCF of 42 and 105 is 21. The Euclidean algorithm is significantly more efficient than the previous methods for larger numbers, as it avoids the need for extensive factorization or listing.
Understanding the Mathematical Principles
The success of these methods hinges on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers. The prime factorization method leverages this directly. The Euclidean algorithm, while seemingly different, implicitly relies on the same principle because the process of repeated subtraction (or division with remainder) gradually reduces the numbers until the common factors are revealed.
Applications of Finding the HCF
The HCF has numerous applications across various mathematical fields and real-world scenarios:
-
Simplifying Fractions: The HCF allows us to simplify fractions to their lowest terms. For example, the fraction 42/105 can be simplified to 2/5 by dividing both the numerator and the denominator by their HCF, which is 21.
-
Solving Diophantine Equations: These are equations where only integer solutions are sought. The HCF plays a crucial role in determining the solvability of certain types of Diophantine equations.
-
Modular Arithmetic: In modular arithmetic, the HCF is essential for determining the existence and nature of solutions to congruences.
-
Cryptography: Concepts related to the HCF, such as relatively prime numbers (numbers with an HCF of 1), are fundamental in various cryptographic algorithms.
-
Geometry: The HCF can be used to find the greatest common measure of lengths in geometric problems.
Frequently Asked Questions (FAQ)
Q: What if the HCF of two numbers is 1?
A: If the HCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the HCF be negative?
A: Although we typically express the HCF as a positive integer, the concept of the GCD can be extended to negative numbers. The absolute value of the HCF will always be the same.
Q: Which method is the best for finding the HCF?
A: The best method depends on the numbers involved. For small numbers, listing factors or prime factorization can be efficient. For larger numbers, the Euclidean algorithm is generally the most efficient and computationally less intensive.
Q: Can I find the HCF of more than two numbers?
A: Yes, you can extend these methods to find the HCF of more than two numbers. For prime factorization, you would find the prime factorization of each number and then identify the common factors. For the Euclidean algorithm, you would find the HCF of two numbers and then find the HCF of that result and the next number, and so on.
Conclusion
Finding the HCF of 42 and 105, as demonstrated through prime factorization, listing factors, and the Euclidean algorithm, highlights the importance of understanding fundamental mathematical concepts. The ability to calculate the HCF efficiently is crucial not only for solving basic mathematical problems but also for tackling more advanced concepts in number theory, algebra, and other related fields. Mastering these methods provides a solid foundation for further exploration of mathematical principles and their applications. Remember to choose the method that best suits the numbers you're working with – for larger numbers, the Euclidean algorithm is your best friend!
Latest Posts
Latest Posts
-
Example Of Formal And Informal
Sep 23, 2025
-
5 Letter Words With Begin
Sep 23, 2025
-
Colour That Begins With A
Sep 23, 2025
-
1 Divided By 1 3
Sep 23, 2025
-
171 Cm In Ft Inches
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 42 And 105 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.