Hcf Of 66 And 110
elan
Sep 14, 2025 · 6 min read
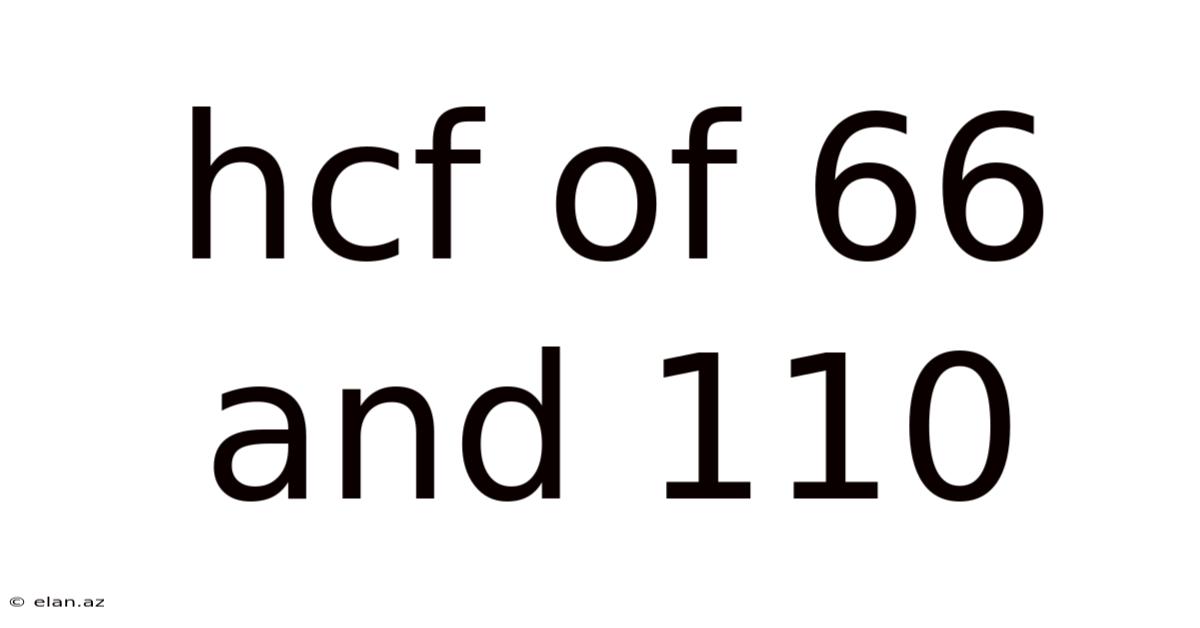
Table of Contents
Unveiling the Secrets of HCF: A Deep Dive into Finding the Highest Common Factor of 66 and 110
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and various methods for calculating the HCF unlocks a deeper appreciation for number theory and its applications in various fields. This comprehensive guide will explore the HCF of 66 and 110, explaining multiple approaches, and delving into the mathematical concepts behind them. We will uncover why finding the HCF is more than just a calculation; it's a fundamental concept with real-world implications.
Introduction: Understanding the Concept of HCF
The highest common factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. It represents the greatest common divisor that these numbers share. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, while the factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The highest among these is 6, therefore the HCF of 12 and 18 is 6. This seemingly simple concept forms the basis for many advanced mathematical operations and has practical applications in various areas, including simplifying fractions, solving problems involving measurement, and even in cryptography.
Method 1: Prime Factorization Method for Finding the HCF of 66 and 110
This method involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). Let's apply this to find the HCF of 66 and 110:
-
Prime Factorization of 66:
66 = 2 × 33 = 2 × 3 × 11
-
Prime Factorization of 110:
110 = 2 × 55 = 2 × 5 × 11
-
Identifying Common Factors:
Both 66 and 110 share the prime factors 2 and 11.
-
Calculating the HCF:
The HCF is the product of the common prime factors. Therefore, the HCF of 66 and 110 is 2 × 11 = 22.
Method 2: Division Method (Euclidean Algorithm) for Finding the HCF of 66 and 110
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers. It relies on repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the HCF. Let's illustrate this with 66 and 110:
-
Divide the larger number (110) by the smaller number (66):
110 ÷ 66 = 1 with a remainder of 44
-
Replace the larger number with the smaller number (66) and the smaller number with the remainder (44):
66 ÷ 44 = 1 with a remainder of 22
-
Repeat the process:
44 ÷ 22 = 2 with a remainder of 0
-
The HCF is the last non-zero remainder:
The last non-zero remainder is 22. Therefore, the HCF of 66 and 110 is 22.
Method 3: Listing Factors Method for Finding the HCF of 66 and 110
This method involves listing all the factors of each number and identifying the largest common factor. While straightforward for smaller numbers, it becomes less efficient for larger numbers.
-
Factors of 66: 1, 2, 3, 6, 11, 22, 33, 66
-
Factors of 110: 1, 2, 5, 10, 11, 22, 55, 110
-
Common Factors: 1, 2, 11, 22
-
Highest Common Factor: The highest common factor is 22.
Comparison of Methods:
Each method offers a different approach to finding the HCF. The prime factorization method provides a deeper understanding of the number's structure, while the Euclidean algorithm is computationally efficient, especially for larger numbers. The listing factors method is simple but becomes impractical for larger numbers. The Euclidean algorithm is generally preferred for its efficiency and ease of application, even with large numbers.
Mathematical Explanation and Significance of HCF
The HCF is a fundamental concept in number theory with several significant implications:
-
Simplifying Fractions: The HCF is crucial for simplifying fractions to their lowest terms. Dividing both the numerator and the denominator by their HCF results in an equivalent fraction in its simplest form.
-
Greatest Common Divisor: The term "greatest common divisor" (GCD) is synonymous with HCF. It emphasizes that the HCF is the largest integer that divides both numbers without leaving a remainder.
-
Modular Arithmetic: The HCF plays a significant role in modular arithmetic, a branch of number theory dealing with remainders. Concepts like modular inverses and solving congruences depend on the HCF.
-
Applications in Cryptography: The HCF, along with other number-theoretic concepts, underpins many cryptographic algorithms, ensuring secure data transmission and storage.
-
Geometric Applications: HCF is used to solve problems related to finding the largest possible square tile that can be used to completely cover a rectangular area without any gaps or overlaps.
Real-World Applications of HCF
Beyond the theoretical aspects, the HCF finds practical applications in various scenarios:
-
Measurement and Division: Imagine you have two ropes of lengths 66 cm and 110 cm. You want to cut them into pieces of equal length, maximizing the length of each piece. The HCF (22 cm) gives you the longest possible length of each piece without any leftover material.
-
Resource Allocation: Suppose you have 66 apples and 110 oranges. You want to divide them into identical gift bags, maximizing the number of bags with the same number of apples and oranges in each. The HCF (22) indicates you can create 22 gift bags, each containing 3 apples and 5 oranges.
-
Scheduling and Synchronization: The HCF can help determine the optimal time intervals for recurring events. For example, if two machines operate on cycles of 66 and 110 seconds respectively, the HCF (22 seconds) indicates the shortest interval at which both machines will simultaneously complete their cycles.
Frequently Asked Questions (FAQ)
-
What if the HCF of two numbers is 1? If the HCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
-
Can the HCF of two numbers be larger than either of the numbers? No, the HCF can never be larger than the smaller of the two numbers.
-
What is the difference between HCF and LCM? The HCF (highest common factor) is the largest number that divides both numbers, while the LCM (least common multiple) is the smallest number that is a multiple of both numbers. For any two numbers, the product of the HCF and LCM is equal to the product of the two numbers.
-
Are there other methods to find the HCF? Yes, there are other less common methods, including using the ladder method or the continued fraction method. However, the prime factorization and Euclidean algorithms are the most widely used and efficient.
Conclusion: The Enduring Relevance of HCF
Finding the HCF, although seemingly a basic arithmetic operation, underpins many advanced mathematical concepts and has far-reaching practical applications. Understanding the various methods for calculating the HCF, such as the prime factorization method and the efficient Euclidean algorithm, allows for a deeper appreciation of its significance. From simplifying fractions to solving complex problems in various fields, the HCF remains an indispensable tool in mathematics and beyond. Its importance extends to our everyday lives, demonstrating how seemingly simple concepts can have significant real-world impact. The HCF of 66 and 110, being 22, is not just a numerical result; it's a gateway to understanding a fundamental concept in mathematics.
Latest Posts
Latest Posts
-
Logarithm Rules A Level Maths
Sep 14, 2025
-
Perimeter Of Half Circle Calculator
Sep 14, 2025
-
The Schoolboy By William Blake
Sep 14, 2025
-
What Is An Nth Term
Sep 14, 2025
-
Nice Words Start With A
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 66 And 110 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.