Increase 52 By 14 Percent
elan
Sep 19, 2025 · 5 min read
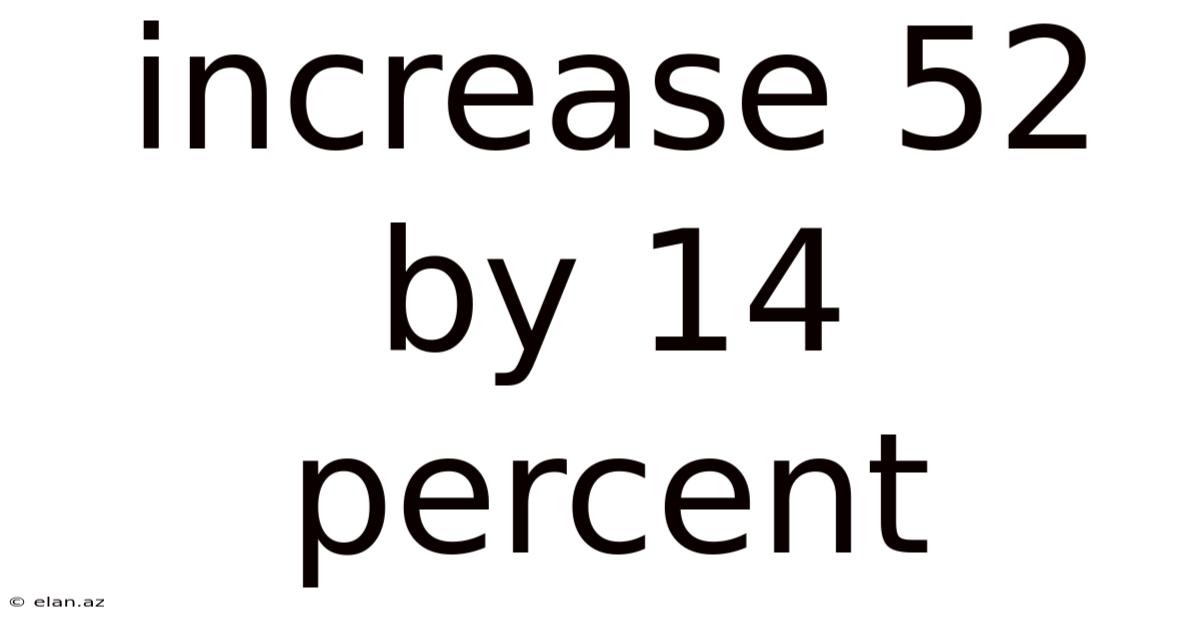
Table of Contents
Increasing 52 by 14 Percent: A Comprehensive Guide
This article will guide you through the process of calculating a 14% increase on the number 52. We'll explore different methods, delve into the underlying mathematical principles, and provide practical applications to help you grasp this fundamental concept in percentage calculations. This guide is designed for everyone, from students brushing up on their math skills to professionals needing to perform quick percentage calculations in their daily work. Understanding percentage increases is crucial in various fields, including finance, statistics, and everyday life scenarios like calculating discounts, tips, or tax increases.
Understanding Percentage Increase
Before we dive into the calculation, let's solidify our understanding of percentage increases. A percentage increase represents the relative growth of a quantity. It expresses how much a number has increased in relation to its original value, expressed as a percentage. The formula for calculating a percentage increase is:
(Increase / Original Value) x 100%
The "Increase" is the difference between the new value and the original value. In simpler terms, it answers the question: "How much bigger is the new number than the original number?"
Method 1: Calculating the Increase Directly
This method involves first calculating the 14% of 52, and then adding this value to the original number.
Step 1: Calculate 14% of 52
To find 14% of 52, we convert the percentage to a decimal by dividing it by 100: 14% = 14/100 = 0.14.
Now, we multiply this decimal by the original value: 0.14 x 52 = 7.28
This means that 14% of 52 is 7.28.
Step 2: Add the Increase to the Original Value
The next step is simply adding the increase (7.28) to the original value (52):
52 + 7.28 = 59.28
Therefore, increasing 52 by 14% results in 59.28.
Method 2: The Multiplier Method
This method is more efficient, especially for more complex percentage calculations. It involves finding a multiplier that represents the original value plus the percentage increase.
Step 1: Find the Multiplier
A 14% increase means the final value is 100% + 14% = 114% of the original value. Converting this to a decimal, we get 114/100 = 1.14. This 1.14 acts as our multiplier.
Step 2: Multiply the Original Value by the Multiplier
Now, we multiply the original value (52) by the multiplier (1.14):
52 x 1.14 = 59.28
This directly gives us the final value after the 14% increase, which is again 59.28.
Comparing the Methods
Both methods yield the same result. The first method is more intuitive for beginners, explicitly showing the calculation of the increase. The second method (multiplier method) is generally faster and more efficient, especially when dealing with multiple percentage changes or more complex scenarios. It's a valuable technique to master for quicker calculations.
Practical Applications and Real-World Scenarios
Percentage increases are used extensively in various real-world situations. Here are a few examples:
-
Finance: Calculating compound interest, inflation adjustments, investment returns, and loan repayments all involve percentage increases. Understanding how to calculate these increases is crucial for making sound financial decisions. For instance, if your investment increases by 14%, you can use this method to determine your new investment value.
-
Sales and Marketing: Calculating sales tax, discounts, markups, and profit margins rely heavily on percentage calculations. Businesses use these calculations to determine selling prices, assess profitability, and analyze sales trends. For example, a store might increase the price of an item by 14% to achieve a desired profit margin.
-
Statistics: Percentage increases are used extensively in data analysis to represent growth rates, changes in population, and other trends. Researchers and analysts use these calculations to interpret data and draw conclusions. For example, the growth rate of a company's revenue can be expressed as a percentage increase.
-
Everyday Life: Calculating tips in restaurants, determining the final price after a sales tax increase, or understanding salary increases all involve percentage calculations. These are common applications that demonstrate the practical relevance of understanding percentage increases in our daily lives.
Expanding the Concept: Decreases and Multiple Increases
The principles discussed here can be easily adapted to calculate percentage decreases. Instead of adding the percentage increase to the original value, you would subtract it. For a 14% decrease, the multiplier would be 1 - 0.14 = 0.86.
Furthermore, the multiplier method proves exceptionally useful when dealing with multiple consecutive percentage increases. Instead of calculating each increase individually, you can multiply the original value by a series of multipliers, each representing a specific percentage change. This significantly simplifies the process and reduces the risk of errors. For instance, if you had a 10% increase followed by a 5% increase, you would multiply the original value by 1.10 and then by 1.05.
Frequently Asked Questions (FAQ)
Q: What if I need to increase a number by a percentage that is not a whole number, say 14.5%?
A: The process remains the same. Simply convert the percentage (14.5%) to a decimal (0.145) and use either method described above. The multiplier method would be 1 + 0.145 = 1.145.
Q: Can I use a calculator to perform these calculations?
A: Absolutely! Calculators are highly recommended for quick and accurate results, especially with more complex percentage calculations. Most calculators will have a percentage function (%) that simplifies the process.
Q: Are there any online tools or software that can help with percentage calculations?
A: Yes, many websites and software programs provide percentage calculators. These tools can be particularly helpful for complex calculations or for repeated calculations of the same type.
Q: What if the original number is a decimal or a fraction?
A: The methods still apply. You would simply treat the decimal or fraction as the original value in the calculations. For example, if your original number is 52.5, you would multiply 52.5 by 1.14 for a 14% increase.
Conclusion
Calculating a 14% increase on 52, or any number for that matter, is a fundamental skill applicable in numerous aspects of life. Mastering both the direct addition and multiplier methods equips you with efficient tools for tackling various percentage-based problems. The multiplier method, in particular, offers a streamlined approach, especially for dealing with multiple percentage changes. Remember that understanding the underlying mathematical principles is key to not only performing calculations correctly but also applying this knowledge effectively in real-world situations. By understanding these methods, you can confidently navigate percentage calculations in your academic pursuits, professional endeavors, and everyday life. The ability to perform these calculations accurately is a valuable skill that will continue to serve you well throughout your life.
Latest Posts
Latest Posts
-
Properties Of A Sedimentary Rock
Sep 20, 2025
-
Words That End With Oa
Sep 20, 2025
-
Linear Interpolation A Level Maths
Sep 20, 2025
-
Example Of A Alternative Hypothesis
Sep 20, 2025
-
Cm 2 To Mm 2
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Increase 52 By 14 Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.