Integral Of 1 X 3
elan
Sep 21, 2025 · 6 min read
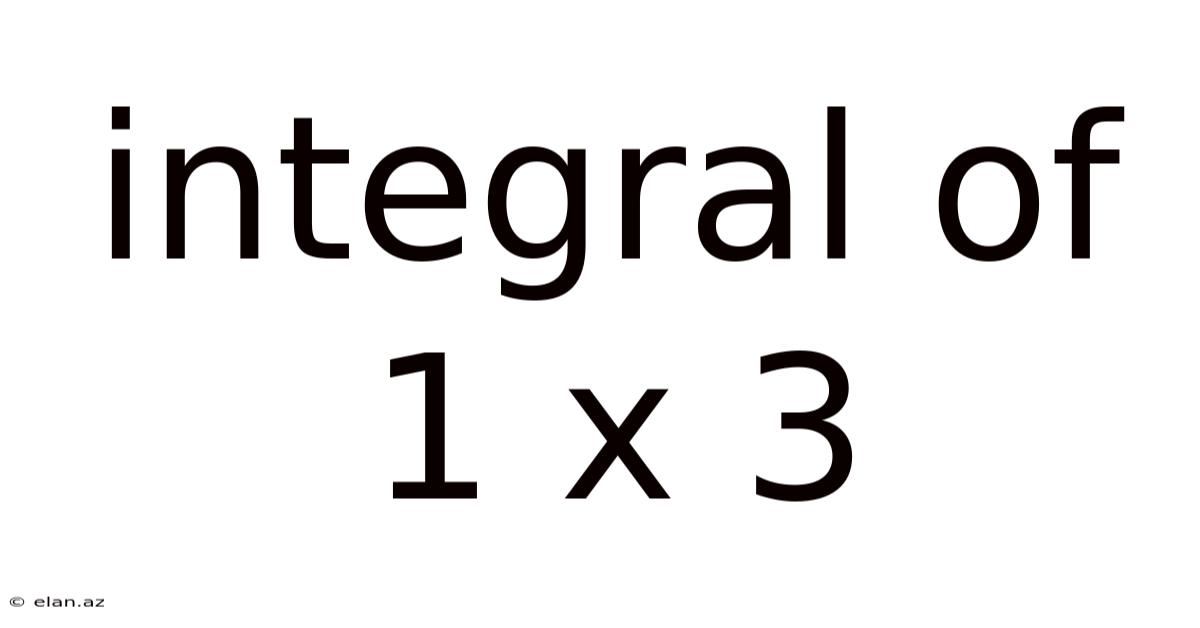
Table of Contents
Understanding and Solving the Integral of 1/(x³): A Comprehensive Guide
The integral of 1/x³, often written as ∫(1/x³)dx, is a fundamental concept in calculus. This article provides a comprehensive guide to solving this integral, explaining the process step-by-step, exploring the underlying mathematical principles, and addressing common questions. We will delve into the power rule of integration, discuss the constant of integration, and even touch upon applications of this integral in various fields. Understanding this seemingly simple integral unlocks a deeper understanding of more complex integration problems.
Introduction: The Power Rule and its Application
The core concept behind solving this integral is the power rule of integration. This rule states that the integral of x<sup>n</sup> (where n is any real number except -1) is (x<sup>n+1</sup>)/(n+1) + C, where C is the constant of integration. Let's apply this rule to our problem: ∫(1/x³)dx.
First, we rewrite 1/x³ as x<sup>-3</sup>. This makes applying the power rule much easier. Our integral now becomes:
∫x<sup>-3</sup>dx
Now, we can directly apply the power rule:
n = -3
(x<sup>n+1</sup>)/(n+1) + C = (x<sup>-3+1</sup>)/(-3+1) + C = (x<sup>-2</sup>)/(-2) + C
Simplifying this expression, we get:
-1/(2x²) + C
Therefore, the integral of 1/x³ is -1/(2x²) + C. The constant of integration, C, is crucial because the derivative of any constant is zero. This means many functions can have the same derivative. The constant C accounts for this family of functions.
Step-by-Step Solution with Detailed Explanation
Let's break down the solution into clear steps to enhance understanding:
-
Rewrite the integrand: The first step is to rewrite the given integral ∫(1/x³)dx in a more manageable form using negative exponents. This gives us ∫x<sup>-3</sup>dx.
-
Apply the power rule: The power rule of integration, as mentioned earlier, states that ∫x<sup>n</sup>dx = (x<sup>n+1</sup>)/(n+1) + C, where n ≠ -1. In our case, n = -3. Applying the rule directly, we obtain:
(x<sup>-3+1</sup>)/(-3+1) + C
-
Simplify the expression: Simplify the exponent and the denominator:
(x<sup>-2</sup>)/(-2) + C
-
Rewrite with a positive exponent: It's generally preferred to express the result with positive exponents. We can rewrite x<sup>-2</sup> as 1/x²:
-1/(2x²) + C
This final expression, -1/(2x²) + C, represents the indefinite integral of 1/x³.
The Significance of the Constant of Integration (C)
The constant of integration, C, is often overlooked, but it's a crucial part of the solution. It represents an entire family of functions, all of which have the same derivative. Consider the following functions:
- -1/(2x²) + 1
- -1/(2x²) + 5
- -1/(2x²) - 2
All these functions, when differentiated, will result in x<sup>-3</sup> or 1/x³. The constant C accounts for this ambiguity. The value of C can be determined only if we are given specific boundary conditions (definite integral).
Explanation Using Differential Calculus
We can verify our integral solution using differential calculus. If our integral is correct, then the derivative of the result should be the original integrand. Let's differentiate -1/(2x²) + C:
d/dx [-1/(2x²) + C] = d/dx [-1/2 * x<sup>-2</sup> + C]
Using the power rule of differentiation, which states that d/dx[x<sup>n</sup>] = nx<sup>n-1</sup>, we get:
(-1/2)(-2)x<sup>-2-1</sup> + 0 = x<sup>-3</sup> = 1/x³
This confirms that our integral solution, -1/(2x²) + C, is correct.
Definite Integral of 1/x³
While the above discussion focuses on the indefinite integral, we can also evaluate the definite integral of 1/x³ over a specific interval [a, b], where a and b are the limits of integration. The definite integral is calculated as:
∫<sub>a</sub><sup>b</sup> x<sup>-3</sup>dx = [-1/(2x²)]<sub>a</sub><sup>b</sup> = [-1/(2b²)] - [-1/(2a²)] = 1/(2a²) - 1/(2b²)
This gives us the exact numerical value of the area under the curve of 1/x³ between points a and b. However, it's important to note that the function 1/x³ is undefined at x = 0. Therefore, the interval [a, b] must not include 0.
Applications of the Integral of 1/x³
The integral of 1/x³ has various applications in different scientific and engineering fields. Some examples include:
- Physics: Calculating work done by a force that varies inversely with the cube of the distance.
- Engineering: Determining the stress distribution in certain types of structures.
- Fluid Mechanics: Solving problems involving fluid flow with a velocity profile related to the inverse cube of a variable.
Frequently Asked Questions (FAQ)
Q1: What happens if we try to apply the power rule when n = -1?
A1: The power rule is not applicable when n = -1 because the denominator (n+1) would become zero, resulting in an undefined expression. The integral of 1/x (when n = -1) is ln|x| + C, where ln denotes the natural logarithm.
Q2: Why is the absolute value used in the integral of 1/x?
A2: The absolute value is used because the natural logarithm is only defined for positive arguments. The absolute value ensures that the argument remains positive regardless of the sign of x.
Q3: Can the constant of integration, C, be zero?
A3: Yes, the constant of integration can be zero. It simply means that one particular function from the family of functions is selected.
Q4: How do I find the value of C in a definite integral?
A4: The constant of integration, C, cancels out when evaluating a definite integral using the fundamental theorem of calculus. You don't need to determine C for definite integrals.
Q5: What if the integrand is more complex, such as ∫(2/x³ + 5x²)dx?
A5: You can solve such integrals using the linearity property of integration. This allows you to break the integral into simpler parts:
∫(2/x³ + 5x²)dx = 2∫x<sup>-3</sup>dx + 5∫x²dx
Solve each part separately using the power rule, and then add the results together.
Conclusion: Mastering Integration Techniques
The integral of 1/x³, while seemingly simple, provides a foundational understanding of integral calculus. Mastering this concept, including the power rule, the significance of the constant of integration, and the distinction between definite and indefinite integrals, will pave the way for solving more complex integration problems. Remember to practice regularly to develop a strong grasp of these fundamental principles. With consistent effort and practice, you'll become proficient in tackling various integration challenges. This detailed guide aims not only to provide the solution but also to provide a comprehensive understanding of the underlying concepts. Through understanding the nuances of the constant of integration, the power rule's limitations, and the applications of this specific integral, a more robust foundation in calculus is built.
Latest Posts
Latest Posts
-
Transformer What Does It Do
Sep 21, 2025
-
Lots Of Words That Rhyme
Sep 21, 2025
-
How High Is 40 Meters
Sep 21, 2025
-
5 Letter Words With Oa
Sep 21, 2025
-
Chemical Formula Of Sodium Sulfate
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.