Integrate Cos X Sin X
elan
Sep 15, 2025 · 6 min read
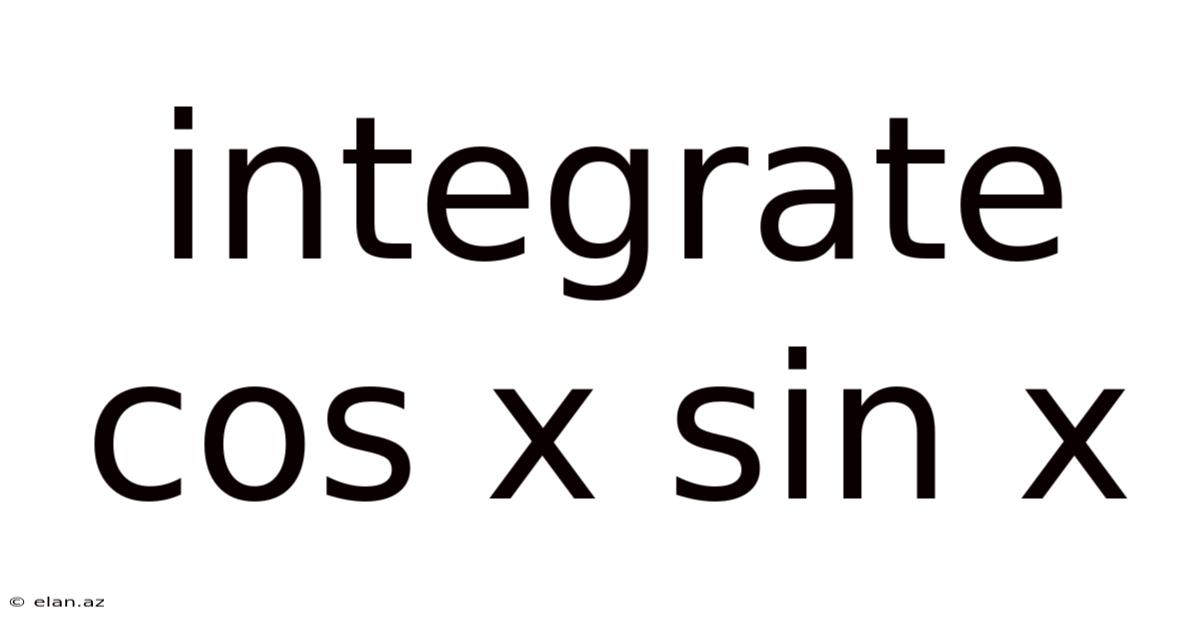
Table of Contents
Integrating cos x sin x: A Comprehensive Guide
Integrating trigonometric functions is a cornerstone of calculus, frequently appearing in physics, engineering, and other scientific fields. This article provides a comprehensive exploration of integrating cos x sin x, covering various methods, underlying principles, and practical applications. We'll delve into different approaches, offering detailed explanations and addressing common questions to solidify your understanding. Mastering this integral will significantly enhance your calculus skills and problem-solving abilities.
Introduction: Understanding the Problem
The integral ∫cos x sin x dx represents a fundamental problem in integration. Unlike simpler integrals involving only sine or cosine, this requires a strategic approach to solve. The key lies in recognizing suitable trigonometric identities and integration techniques to simplify the expression before proceeding with the integration process. We will explore several effective methods, highlighting their strengths and weaknesses.
Method 1: Using the Double Angle Formula
One of the most straightforward methods involves utilizing the double angle formula for sine. Recall the identity:
sin(2x) = 2sin x cos x
Rearranging this equation, we get:
sin x cos x = (1/2)sin(2x)
Substituting this into our integral, we obtain:
∫cos x sin x dx = ∫(1/2)sin(2x) dx
This integral is now easily solvable using a simple u-substitution. Let u = 2x, then du = 2dx, and dx = (1/2)du. The integral becomes:
(1/2)∫sin u * (1/2) du = (1/4)∫sin u du
Integrating sin u, we get -cos u. Substituting back for u, we have:
(1/4)(-cos(2x)) + C
Therefore, the final result is:
∫cos x sin x dx = -(1/4)cos(2x) + C, where C is the constant of integration.
Method 2: Integration by Parts
Integration by parts is a powerful technique that can be applied to a wide range of integrals. The formula for integration by parts is:
∫u dv = uv - ∫v du
For our integral, let's choose:
u = sin x => du = cos x dx dv = cos x dx => v = sin x
Applying the integration by parts formula:
∫cos x sin x dx = sin x * sin x - ∫sin x * cos x dx
Notice that the integral on the right-hand side is the same as the original integral. Let's denote this integral as I:
I = sin²x - I
Adding I to both sides:
2I = sin²x
I = (1/2)sin²x + C
This seems different from the result we obtained using the double angle formula. However, using the trigonometric identity cos(2x) = 1 - 2sin²x, we can show they are equivalent. Solving for sin²x:
sin²x = (1 - cos(2x))/2
Substituting this into our result:
I = (1/2)((1 - cos(2x))/2) + C = (1/4)(1 - cos(2x)) + C = (1/4) - (1/4)cos(2x) + C
The constant (1/4) can be absorbed into the constant of integration, giving us the same result as before:
∫cos x sin x dx = -(1/4)cos(2x) + C
Method 3: Using Substitution with a Trigonometric Identity
Another approach leverages a different trigonometric identity. We know that:
cos²x + sin²x = 1
We can rewrite our integral as:
∫cos x sin x dx = ∫cos x * sin x dx
Let u = sin x. Then du = cos x dx. Substituting:
∫u du = (1/2)u² + C
Substituting back for u:
(1/2)sin²x + C
Again, this seems different at first glance. But, remembering that sin²x = (1 - cos(2x))/2, we arrive at the same final answer:
∫cos x sin x dx = -(1/4)cos(2x) + C
Reconciling Different Results: The Constant of Integration
It's crucial to understand that the seemingly different results obtained using various methods are actually equivalent. The difference lies only in the constant of integration, C. Different methods may lead to different expressions for the constant, but these differences are absorbed into the overall constant of integration. The constant of integration accounts for the family of functions that have the same derivative.
Definite Integrals: Applying the Results
When dealing with definite integrals, the constant of integration cancels out. For example, if we want to evaluate:
∫(from 0 to π/2) cos x sin x dx
Using any of the derived formulas, we get:
= -(1/4)cos(π) - (-(1/4)cos(0)) = (1/4) + (1/4) = 1/2
Explanation of the Trigonometric Identities Used
The success of the integration methods heavily relies on the utilization of key trigonometric identities. Understanding these identities is vital for mastering trigonometric integration.
-
Double Angle Formula for Sine: sin(2x) = 2sin x cos x. This identity provides a direct substitution to simplify the integrand.
-
Pythagorean Identity: cos²x + sin²x = 1. While not directly used for substitution in one of the methods, understanding this identity is crucial for trigonometric manipulations and recognizing equivalent forms of solutions.
-
Double Angle Formula for Cosine: cos(2x) = cos²x - sin²x = 1 - 2sin²x = 2cos²x - 1. This identity is essential for showing the equivalence of the different results obtained through various integration techniques.
Practical Applications
The integral of cos x sin x has numerous applications in various fields:
-
Physics: Solving problems involving oscillatory motion, such as the motion of a pendulum or a mass-spring system. The integral often appears when calculating energy or work related to these systems.
-
Engineering: Analyzing AC circuits, where sinusoidal waveforms are prevalent. The integral can be crucial for calculating power, current, or voltage in such circuits.
-
Signal Processing: Processing and analyzing signals with sinusoidal components. The integral is used in various signal processing techniques, including Fourier analysis.
-
Probability and Statistics: In probability distributions involving trigonometric functions.
Frequently Asked Questions (FAQ)
Q: Can I use other methods to solve this integral?
A: While the methods discussed are among the most efficient, other techniques like using complex exponentials or power series expansions are theoretically possible but often more cumbersome for this specific integral.
Q: Why is the constant of integration important?
A: The constant of integration represents the family of functions that share the same derivative. Omitting it leads to an incomplete and inaccurate solution.
Q: What if the integral is ∫cos(ax)sin(bx)dx?
A: For this more general case, the double angle formula isn't directly applicable. Methods involving trigonometric product-to-sum identities become necessary. These identities allow you to express the product of sine and cosine functions as a sum of simpler trigonometric functions that are readily integrable.
Q: Are there any online tools or calculators that can verify my solution?
A: While many online integral calculators exist, it's crucial to understand the underlying principles and methods rather than relying solely on computational tools. These calculators can provide a quick check, but mastering the techniques is key to solving more complex problems.
Conclusion
Integrating cos x sin x offers a valuable learning opportunity in calculus, emphasizing the importance of strategic application of trigonometric identities and integration techniques. We've explored multiple methods, each offering a unique perspective on solving this integral, and highlighted the equivalence of seemingly disparate solutions. By understanding these methods, their underlying principles, and the importance of the constant of integration, you've significantly broadened your problem-solving capabilities in calculus and related fields. Remember to practice these techniques to build your confidence and mastery of integration. The ability to tackle integrals like this is a testament to your growing proficiency in calculus, opening doors to tackling even more complex mathematical challenges in your future endeavors.
Latest Posts
Latest Posts
-
Higher English Persuasive Essay Topics
Sep 15, 2025
-
Ideas For English Speaking Exam
Sep 15, 2025
-
Meaning Of Burst Your Bubble
Sep 15, 2025
-
Derivative Of Ln 1 X
Sep 15, 2025
-
Mammals Amphibians Reptiles Birds Fish
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Integrate Cos X Sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.