Is 1/2 Greater Than 3/4
elan
Sep 13, 2025 · 6 min read
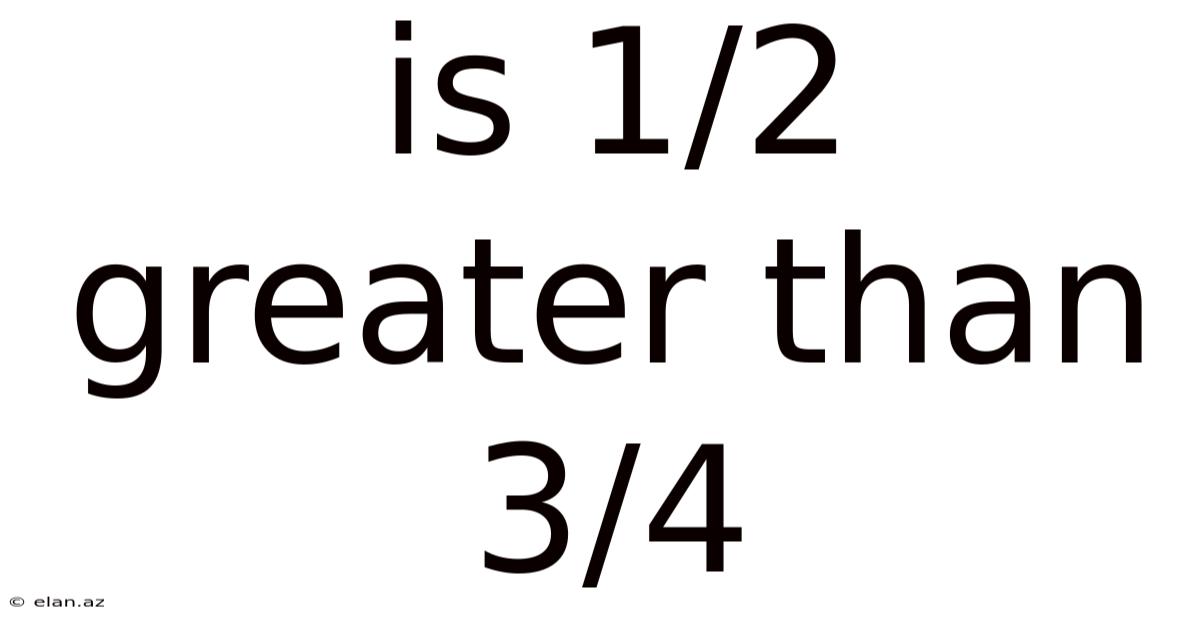
Table of Contents
Is 1/2 Greater Than 3/4? Understanding Fractions and Comparisons
Is 1/2 greater than 3/4? The answer, at first glance, might seem obvious. This article delves deeper than a simple "yes" or "no," exploring the fundamental concepts of fractions, providing multiple methods for comparing them, and ultimately building a solid understanding of fractional relationships. Understanding fractions is crucial for various aspects of life, from baking and cooking to advanced mathematics and scientific calculations. This comprehensive guide will equip you with the tools to confidently compare fractions and tackle more complex mathematical problems.
Introduction to Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator shows how many equal parts the whole is divided into. For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) indicates that the whole is divided into two equal parts. Therefore, 1/2 represents one-half of a whole.
Understanding fractions is pivotal in various fields. From dividing a pizza among friends to calculating proportions in chemistry or engineering, the ability to compare and manipulate fractions is essential. This article will focus on comparing fractions, specifically addressing whether 1/2 is greater than 3/4.
Comparing 1/2 and 3/4: Visual Representation
One of the easiest ways to compare fractions is through visual representation. Imagine two identical circles.
-
Circle 1: Divide this circle into two equal halves. Shade one half. This visually represents 1/2.
-
Circle 2: Divide this circle into four equal quarters. Shade three quarters. This visually represents 3/4.
By comparing the shaded areas of both circles, it becomes immediately clear that the shaded area representing 3/4 is larger than the shaded area representing 1/2. Therefore, 3/4 is greater than 1/2.
Comparing 1/2 and 3/4: Finding a Common Denominator
A more mathematical approach involves finding a common denominator. This means finding a number that is a multiple of both denominators (2 and 4 in this case). The least common multiple of 2 and 4 is 4.
- We can convert 1/2 to an equivalent fraction with a denominator of 4 by multiplying both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4
Now we can easily compare 2/4 and 3/4. Since they have the same denominator, we can compare their numerators directly. 3 is greater than 2, so 3/4 is greater than 2/4 (which is equivalent to 1/2).
Comparing 1/2 and 3/4: Decimal Conversion
Another method is to convert both fractions into decimals. This involves dividing the numerator by the denominator.
-
1/2 = 1 ÷ 2 = 0.5
-
3/4 = 3 ÷ 4 = 0.75
By comparing the decimal values, we see that 0.75 is greater than 0.5. Therefore, 3/4 is greater than 1/2.
Comparing Fractions: A General Approach
The methods used above can be applied to compare any two fractions. Here's a general approach:
-
Find a common denominator: This is often the easiest and most reliable method. Find the least common multiple (LCM) of the denominators. Convert both fractions to equivalent fractions with the common denominator.
-
Compare the numerators: Once the denominators are the same, the fraction with the larger numerator is the greater fraction.
-
Convert to decimals: Dividing the numerator by the denominator for each fraction will give you their decimal equivalents. Compare the decimal values to determine which fraction is greater.
-
Visual representation: While not always practical for complex fractions, visually representing the fractions can be helpful for understanding the relationships.
Why Understanding Fraction Comparison is Important
The ability to compare fractions is crucial for a range of applications:
-
Everyday Life: Dividing resources fairly, understanding discounts and sales, and even cooking and baking all involve working with fractions.
-
Mathematics: Fraction comparison is a fundamental building block for more advanced mathematical concepts, such as algebra, geometry, and calculus.
-
Science: Many scientific calculations and measurements involve fractions and proportions. Understanding how to compare them is essential for accurate analysis and interpretation of data.
-
Technology: Computer programming, engineering, and other technical fields often rely on fractional calculations and comparisons.
Frequently Asked Questions (FAQ)
Q: Can I always find a common denominator?
A: Yes, you can always find a common denominator for any two fractions. The least common denominator is the smallest number that is a multiple of both denominators. However, sometimes finding the least common multiple can be time-consuming for large numbers. In such cases, any common multiple will work, although it might make the numbers larger and the calculation slightly more complex.
Q: Is there a quick way to compare fractions without finding a common denominator?
A: Sometimes, you can compare fractions quickly by visually inspecting them. For example, if one fraction has a larger numerator and a smaller denominator than another fraction, it is likely to be larger. However, this is not a foolproof method and can lead to errors, so it's always best to use a more rigorous method like finding a common denominator or converting to decimals for accurate comparison.
Q: What if the fractions are negative?
A: When comparing negative fractions, remember that the larger the magnitude (absolute value) of the negative fraction, the smaller the fraction's value. For example, -1/2 is greater than -3/4 because -1/2 is closer to zero.
Q: What if one fraction is a mixed number and the other is an improper fraction?
A: Convert both fractions to improper fractions before comparing them using the methods discussed above. A mixed number is a combination of a whole number and a fraction (e.g., 1 1/2), while an improper fraction has a numerator that is greater than or equal to the denominator (e.g., 3/2). To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator.
Conclusion
In conclusion, 1/2 is not greater than 3/4. Through visual representation, finding a common denominator, and decimal conversion, we have clearly demonstrated that 3/4 is larger than 1/2. This article has provided multiple methods for comparing fractions, emphasizing the importance of understanding these fundamental mathematical concepts. Mastering the ability to compare fractions is a valuable skill that extends far beyond the classroom, enhancing problem-solving capabilities in various aspects of life. Remember to practice these methods regularly to solidify your understanding and improve your ability to confidently work with fractions. The more you practice, the more intuitive and efficient fraction comparison will become.
Latest Posts
Latest Posts
-
What Metal Is The Lightest
Sep 13, 2025
-
What Is A Cash Book
Sep 13, 2025
-
Plant And Animal Cells Gcse
Sep 13, 2025
-
What Is A File System
Sep 13, 2025
-
Common Noun And Proper Nouns
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Greater Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.