Is 5/16 Larger Than 3/8
elan
Sep 17, 2025 · 5 min read
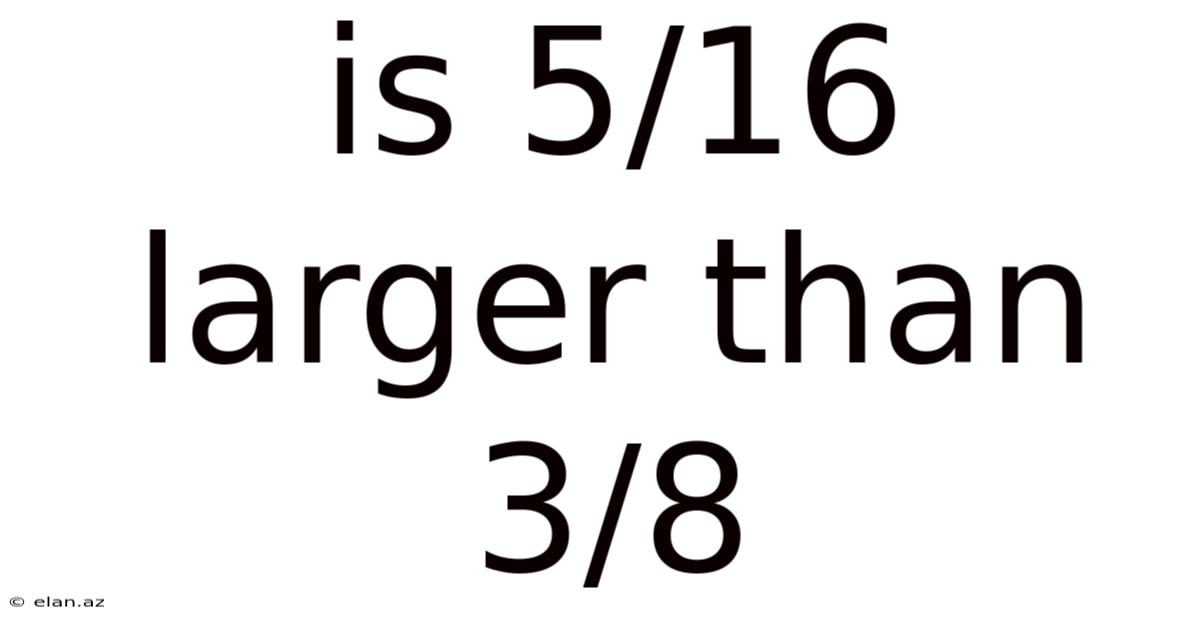
Table of Contents
Is 5/16 Larger Than 3/8? A Deep Dive into Fraction Comparison
Are you struggling with comparing fractions? Many find comparing fractions like 5/16 and 3/8 tricky, but with the right understanding, it becomes straightforward. This article will not only answer the question, "Is 5/16 larger than 3/8?" but also equip you with the skills to confidently compare any two fractions. We'll explore multiple methods, explain the underlying mathematical principles, and address common misconceptions. Let's dive in!
Understanding Fractions
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts you have) and 'b' is the denominator (the total number of equal parts the whole is divided into).
For example, in the fraction 3/8, the numerator is 3 and the denominator is 8. This means we have 3 out of 8 equal parts of a whole.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This means rewriting both fractions so they have the same denominator. Once they have the same denominator, we can simply compare their numerators.
Let's apply this to our problem: Is 5/16 larger than 3/8?
-
Find the least common multiple (LCM) of the denominators: The denominators are 16 and 8. The LCM of 16 and 8 is 16 (because 16 is a multiple of 8).
-
Rewrite the fractions with the common denominator:
- 5/16 already has a denominator of 16, so it remains the same.
- To rewrite 3/8 with a denominator of 16, we multiply both the numerator and the denominator by 2: (3 x 2) / (8 x 2) = 6/16
-
Compare the numerators: Now we compare 5/16 and 6/16. Since 5 < 6, we can conclude that 5/16 < 6/16.
Therefore, 5/16 is NOT larger than 3/8.
Method 2: Converting to Decimals
Another effective method involves converting the fractions to decimals. This is particularly helpful if you're comfortable working with decimal numbers. To convert a fraction to a decimal, simply divide the numerator by the denominator.
-
Convert 5/16 to a decimal: 5 ÷ 16 = 0.3125
-
Convert 3/8 to a decimal: 3 ÷ 8 = 0.375
-
Compare the decimals: Since 0.3125 < 0.375, we conclude that 5/16 < 3/8.
Again, this confirms that 5/16 is NOT larger than 3/8.
Method 3: Visual Representation
While less precise for complex fractions, visualizing the fractions can be helpful, especially for beginners. Imagine a pizza cut into 16 slices (for 5/16) and another pizza cut into 8 slices (for 3/8).
- For 5/16, you have 5 out of 16 slices.
- For 3/8, you have 3 out of 8 slices. Since 8 slices is half a pizza, you have 6 out of 16 slices (because 3/8 is equivalent to 6/16).
Visually comparing 5 slices to 6 slices clearly shows that 6 slices represent a larger portion.
This visual representation further reinforces that 5/16 is smaller than 3/8.
Understanding the Mathematical Principles
The success of both the common denominator and decimal conversion methods lies in the fundamental principle of equivalent fractions. Equivalent fractions represent the same proportion but have different numerators and denominators. For example, 3/8, 6/16, and 9/24 are all equivalent fractions. They all represent the same value (0.375). By finding a common denominator, we're essentially expressing both fractions using the same "unit" of measurement, making the comparison straightforward.
Addressing Common Misconceptions
A common mistake is to simply compare the numerators and denominators individually. This is incorrect. The size of a fraction depends on the ratio between the numerator and the denominator, not their individual values. A larger numerator does not automatically mean a larger fraction. For example, 7/10 is smaller than 9/10, but 1/2 is larger than 1/5.
Extending the Concepts: Comparing More Than Two Fractions
The methods discussed above can be easily extended to compare more than two fractions. For multiple fractions, find the LCM of all the denominators and rewrite all fractions using this common denominator. Then compare the numerators.
Frequently Asked Questions (FAQ)
Q: What if the LCM is difficult to find?
A: While finding the LCM is the most efficient method, if you struggle to find the LCM of larger numbers, the decimal conversion method remains a reliable alternative.
Q: Are there other methods to compare fractions?
A: While less common, methods involving cross-multiplication can also be used. However, for most cases, finding a common denominator or converting to decimals offers greater clarity and simplicity.
Q: Can I simplify fractions before comparing them?
A: Simplifying fractions before comparing them can sometimes make the comparison easier, but it's not always necessary. If you simplify both fractions to their simplest forms, you can then compare them using any of the methods described above. In the case of 5/16 and 3/8, 5/16 is already in its simplest form, while 3/8 is also in its simplest form.
Q: Why is understanding fraction comparison important?
A: Understanding fraction comparison is crucial for numerous applications in mathematics, science, and everyday life. From baking (measuring ingredients) to calculating proportions and understanding data, a firm grasp of fractions is invaluable.
Conclusion
Comparing fractions, such as determining whether 5/16 is larger than 3/8, might seem daunting at first. However, by employing strategies like finding a common denominator or converting to decimals, the process becomes significantly easier and more manageable. Understanding the underlying principles of equivalent fractions and employing visualization techniques can further enhance your comprehension. Mastering fraction comparison is not just about solving mathematical problems; it's about developing a deeper understanding of numerical relationships and their real-world applications. Remember to practice regularly and explore different methods to find the approach that works best for you. With consistent effort and the right techniques, you'll soon become confident in comparing any two fractions.
Latest Posts
Latest Posts
-
Energy Stored By Capacitor Equation
Sep 17, 2025
-
How Far Is 900 Meters
Sep 17, 2025
-
Definition Of Special Purpose Vehicle
Sep 17, 2025
-
2 Out Of 5 Percentage
Sep 17, 2025
-
Do Tigers Live In Jungles
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 5/16 Larger Than 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.