Lcm Of 105 And 130
elan
Sep 18, 2025 · 6 min read
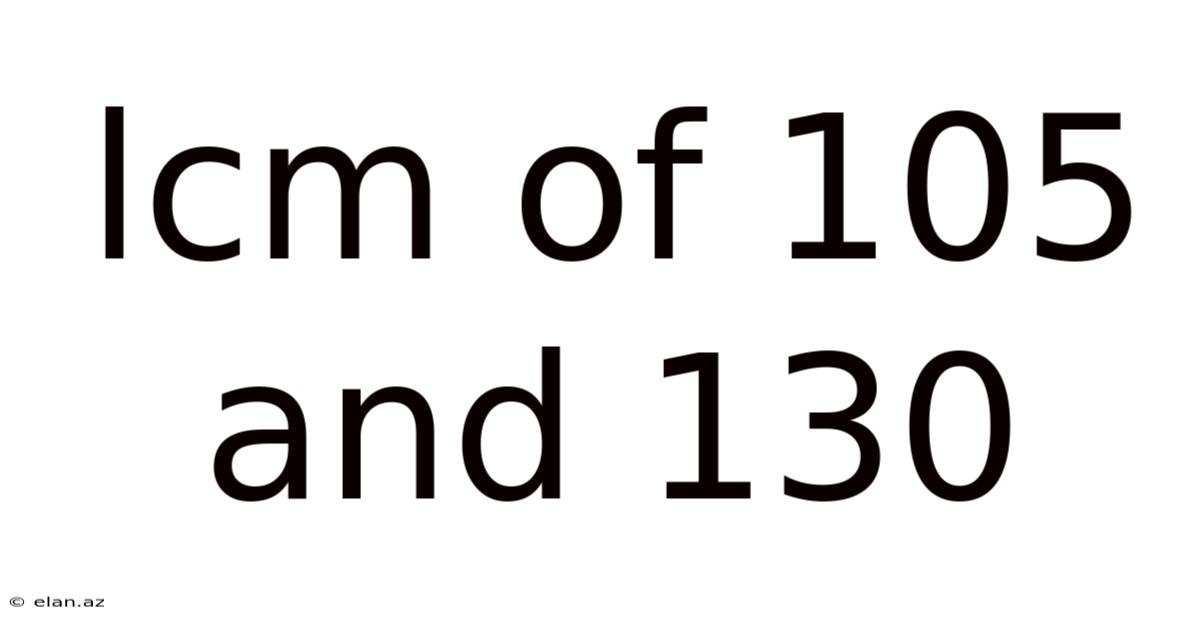
Table of Contents
Finding the LCM of 105 and 130: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving problems in algebra and beyond. This article will delve into the process of calculating the LCM of 105 and 130, exploring different methods and providing a thorough understanding of the underlying principles. We'll cover prime factorization, the least common multiple formula, and even touch upon the relationship between LCM and greatest common divisor (GCD). By the end, you'll not only know the LCM of 105 and 130 but also possess a solid understanding of this important mathematical concept.
Understanding Least Common Multiple (LCM)
Before we dive into the calculation, let's clarify what the least common multiple actually means. The LCM of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both of your original numbers can divide into evenly.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12… Multiples of 3 are 3, 6, 9, 12, 15… The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Prime Factorization
This is arguably the most fundamental and conceptually clear method for finding the LCM. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
1. Find the prime factorization of 105:
105 is divisible by 3 (105/3 = 35). 35 is divisible by 5 (35/5 = 7), and 7 is a prime number. Therefore, the prime factorization of 105 is 3 x 5 x 7.
2. Find the prime factorization of 130:
130 is divisible by 2 (130/2 = 65). 65 is divisible by 5 (65/5 = 13), and 13 is a prime number. Therefore, the prime factorization of 130 is 2 x 5 x 13.
3. Identify common and uncommon prime factors:
Comparing the prime factorizations, we see that both numbers share a common factor of 5. The uncommon factors are 3, 7, 2, and 13.
4. Calculate the LCM:
The LCM is calculated by multiplying each prime factor raised to the highest power it appears in either factorization. In this case:
LCM(105, 130) = 2 x 3 x 5 x 7 x 13 = 2730
Therefore, the least common multiple of 105 and 130 is 2730. This means that 2730 is the smallest number that is divisible by both 105 and 130 without leaving a remainder.
Method 2: Using the Formula LCM(a, b) = (|a x b|) / GCD(a, b)
This method leverages the relationship between the LCM and the greatest common divisor (GCD). The GCD of two numbers is the largest positive integer that divides both numbers without leaving a remainder.
1. Find the GCD of 105 and 130 using the Euclidean Algorithm:
The Euclidean Algorithm is an efficient method for finding the GCD. It involves repeatedly applying the division algorithm until the remainder is 0.
- 130 = 105 x 1 + 25
- 105 = 25 x 4 + 5
- 25 = 5 x 5 + 0
The last non-zero remainder is 5, so the GCD(105, 130) = 5.
2. Apply the LCM formula:
The formula for calculating the LCM using the GCD is:
LCM(a, b) = (|a x b|) / GCD(a, b)
Substituting the values:
LCM(105, 130) = (105 x 130) / 5 = 13650 / 5 = 2730
This method confirms our result from the prime factorization method. The LCM of 105 and 130 is 2730.
Method 3: Listing Multiples (Less Efficient for Larger Numbers)
This method involves listing multiples of each number until a common multiple is found. While simple for smaller numbers, it becomes impractical for larger numbers.
Multiples of 105: 105, 210, 315, 420, 525, 630, 735, 840, 945, 1050, 1155, 1260, 1365, 1470, 1575, 1680, 1785, 1890, 1995, 2100, 2205, 2310, 2415, 2520, 2625, 2730...
Multiples of 130: 130, 260, 390, 520, 650, 780, 910, 1040, 1170, 1300, 1430, 1560, 1690, 1820, 1950, 2080, 2210, 2340, 2470, 2600, 2730...
The smallest common multiple is 2730.
Understanding the Relationship Between LCM and GCD
The relationship between the LCM and GCD is fundamental in number theory. For any two positive integers a and b, the product of their LCM and GCD is always equal to the product of the two numbers themselves. This can be expressed as:
LCM(a, b) x GCD(a, b) = a x b
In our example:
LCM(105, 130) x GCD(105, 130) = 2730 x 5 = 13650
105 x 130 = 13650
This relationship provides a powerful check on the accuracy of your LCM and GCD calculations.
Applications of LCM
The concept of LCM finds practical applications in various areas:
- Fractions: Finding the LCM of the denominators is essential when adding or subtracting fractions.
- Scheduling: Determining when events will occur simultaneously (e.g., buses arriving at a stop).
- Cyclic patterns: Analyzing repeating patterns or cycles in different systems.
- Modular arithmetic: Solving problems related to congruences and remainders.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The Least Common Multiple (LCM) is the smallest number that is a multiple of both given numbers. The Greatest Common Divisor (GCD) is the largest number that divides both given numbers without leaving a remainder.
Q: Can the LCM of two numbers be smaller than one of the numbers?
A: No. The LCM is always greater than or equal to the larger of the two numbers.
Q: Is there a single correct method for finding the LCM?
A: While the prime factorization method is often considered the most fundamental, there are several effective methods, each with its advantages and disadvantages depending on the numbers involved. The method using the GCD is particularly efficient for larger numbers.
Q: What if one of the numbers is zero?
A: The LCM of any number and zero is undefined.
Q: What if the two numbers are the same?
A: If the two numbers are the same, the LCM is simply the number itself.
Conclusion
Finding the LCM of 105 and 130, as demonstrated above, showcases the practical application of fundamental number theory concepts. Whether you use prime factorization, the LCM formula with the GCD, or the method of listing multiples (for smaller numbers), the result remains consistent: the LCM of 105 and 130 is 2730. Understanding the various methods and the relationship between LCM and GCD provides a more comprehensive understanding of these mathematical tools, enabling you to solve a wider range of problems effectively. Remember to choose the method best suited to the context and complexity of the numbers involved. This detailed explanation aims not only to provide the answer but also to equip you with the knowledge and understanding necessary to tackle similar problems independently.
Latest Posts
Latest Posts
-
100 Thousand Naira In Dollars
Sep 18, 2025
-
Meaning Of Threatened In Hindi
Sep 18, 2025
-
Verbs Which End With Y
Sep 18, 2025
-
9 Litre Really Useful Box
Sep 18, 2025
-
Inequality In A Number Line
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 105 And 130 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.