Lcm Of 105 And 462
elan
Sep 17, 2025 · 5 min read
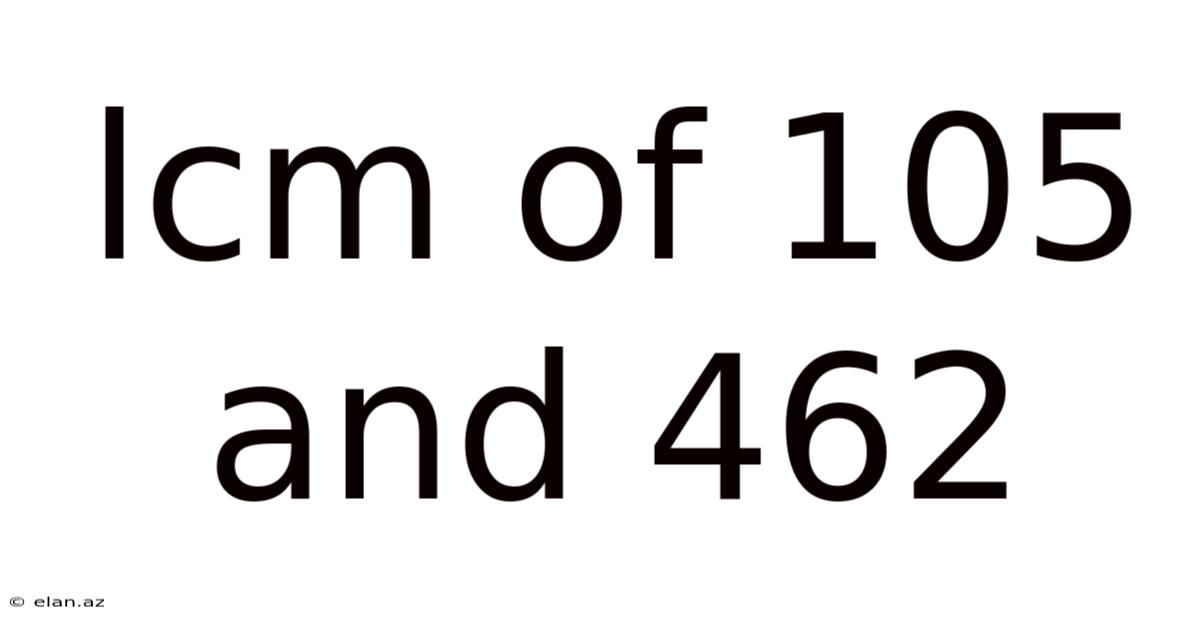
Table of Contents
Finding the Least Common Multiple (LCM) of 105 and 462: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and different methods involved can significantly enhance your mathematical abilities. This article provides a comprehensive guide to calculating the LCM of 105 and 462, exploring various approaches, and explaining the concepts behind them. We’ll delve into prime factorization, the greatest common divisor (GCD), and even discuss real-world applications where LCM calculations prove invaluable. This detailed explanation will equip you with a thorough understanding of LCM and related mathematical concepts.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For instance, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3. Understanding LCM is crucial in various mathematical applications, from simplifying fractions to solving problems involving cycles and periodic events.
Method 1: Prime Factorization
This is arguably the most fundamental method for finding the LCM. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
1. Prime Factorization of 105:
Let's start by finding the prime factors of 105. We can do this through a factor tree or by systematically dividing by prime numbers:
105 ÷ 3 = 35 35 ÷ 5 = 7 7 ÷ 7 = 1
Therefore, the prime factorization of 105 is 3 × 5 × 7.
2. Prime Factorization of 462:
Now let's find the prime factors of 462:
462 ÷ 2 = 231 231 ÷ 3 = 77 77 ÷ 7 = 11 11 ÷ 11 = 1
Therefore, the prime factorization of 462 is 2 × 3 × 7 × 11.
3. Calculating the LCM using Prime Factorization:
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together.
- Prime factors present: 2, 3, 5, 7, 11
- Highest powers: 2¹ (from 462), 3¹ (from both), 5¹ (from 105), 7¹ (from both), 11¹ (from 462)
LCM(105, 462) = 2 × 3 × 5 × 7 × 11 = 2310
Therefore, the least common multiple of 105 and 462 is 2310.
Method 2: Using the Greatest Common Divisor (GCD)
Another efficient method utilizes the relationship between the LCM and the greatest common divisor (GCD). The GCD of two numbers is the largest number that divides both without leaving a remainder. There's a handy formula connecting LCM and GCD:
LCM(a, b) = (a × b) / GCD(a, b)
1. Finding the GCD of 105 and 462:
We can find the GCD using the Euclidean algorithm. This algorithm involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- 462 = 4 × 105 + 42
- 105 = 2 × 42 + 21
- 42 = 2 × 21 + 0
The last non-zero remainder is 21, so the GCD(105, 462) = 21.
2. Calculating the LCM using the GCD:
Now we can use the formula:
LCM(105, 462) = (105 × 462) / 21 = 48510 / 21 = 2310
As expected, we arrive at the same LCM: 2310.
Method 3: Listing Multiples
This method is less efficient for larger numbers but provides a more intuitive understanding of the LCM concept. It involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
Multiples of 105: 105, 210, 315, 420, 525, 630, 735, 840, 945, 1050, 1155, 1260, 1365, 1470, 1575, 1680, 1785, 1890, 1995, 2100, 2205, 2310...
Multiples of 462: 462, 924, 1386, 1848, 2310...
The smallest common multiple is 2310. This method becomes cumbersome for larger numbers, highlighting the efficiency of prime factorization and the GCD method.
Why Learn Different Methods?
While all methods lead to the same result, understanding different approaches offers several advantages:
- Conceptual Understanding: Prime factorization builds a strong foundation in number theory.
- Computational Efficiency: The GCD method is generally faster for larger numbers.
- Problem-Solving Flexibility: Knowing multiple methods equips you to choose the most suitable approach based on the context and the numbers involved.
Real-World Applications of LCM
The concept of LCM isn't confined to the classroom. It finds practical applications in various scenarios:
- Scheduling: Imagine two buses departing from the same station at different intervals. The LCM helps determine when they will depart simultaneously again.
- Gear Ratios: In mechanical engineering, LCM is crucial in calculating gear ratios to synchronize the rotations of different gears.
- Periodic Events: Predicting the simultaneous occurrence of cyclical events, such as planetary alignments or the repetition of specific patterns, often involves LCM calculations.
- Fraction Operations: Finding the least common denominator (LCD) when adding or subtracting fractions is directly related to finding the LCM of the denominators.
Frequently Asked Questions (FAQ)
-
Q: What if one of the numbers is zero? A: The LCM of any number and zero is undefined.
-
Q: Can the LCM of two numbers be equal to one of the numbers? A: Yes, if one number is a multiple of the other. For example, LCM(3, 6) = 6.
-
Q: Is the LCM always larger than both numbers? A: No, it's larger than or equal to the larger of the two numbers. As shown previously, if one number is a factor of the other, the LCM is the larger number.
-
Q: Are there any shortcuts for finding the LCM of larger numbers? A: While prime factorization and the GCD method are generally effective, advanced algorithms exist for finding the LCM of very large numbers efficiently, often employing computational techniques beyond the scope of this article.
Conclusion
Finding the LCM of 105 and 462, as demonstrated through various methods, illustrates the fundamental concepts of number theory. Mastering these methods not only improves your arithmetic skills but also enhances your problem-solving capabilities in diverse fields. Remember that selecting the appropriate method depends on the context and the numbers involved. The understanding gained through exploring different techniques will prove invaluable in tackling more complex mathematical challenges. The LCM of 105 and 462 is definitively 2310, a result validated by multiple approaches. This thorough exploration hopefully provides a clear and complete understanding of LCM calculations.
Latest Posts
Latest Posts
-
How Long Is 26 Inches
Sep 17, 2025
-
Chime Crossword Clue 4 Letters
Sep 17, 2025
-
Body Parts Beginning With S
Sep 17, 2025
-
Solving 2 Step Equations Worksheet
Sep 17, 2025
-
Simple Algebra Questions With Answers
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 105 And 462 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.