Lcm Of 105 And 770
elan
Sep 12, 2025 · 6 min read
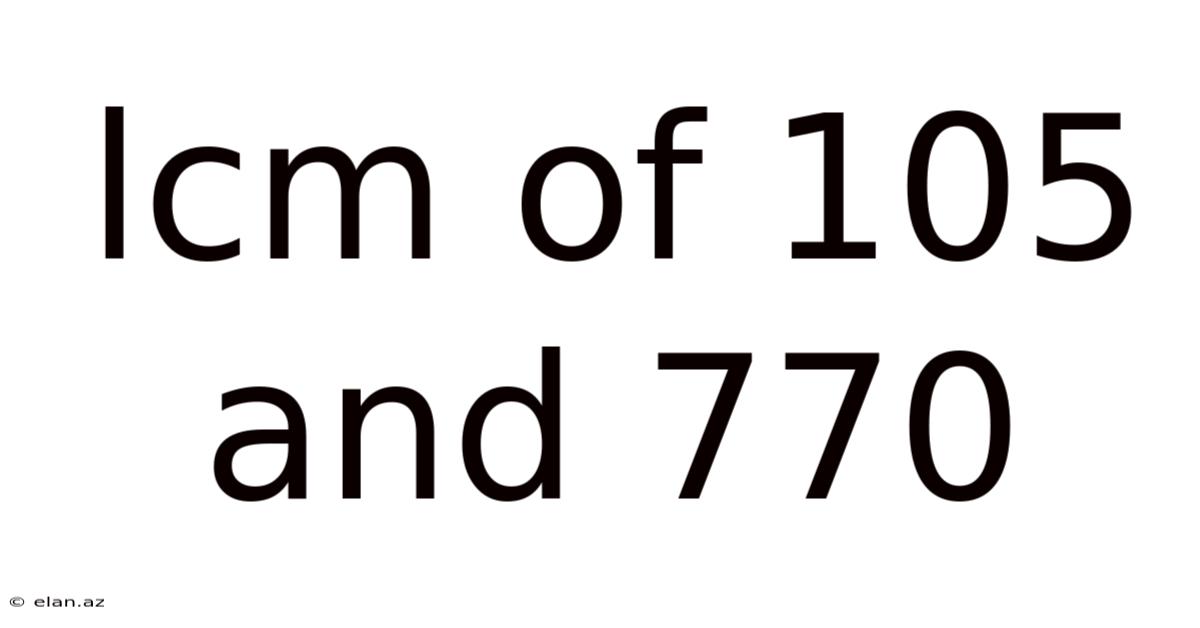
Table of Contents
Finding the Least Common Multiple (LCM) of 105 and 770: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple mathematical task, but understanding the underlying concepts and various methods for calculation can significantly enhance your mathematical problem-solving skills. This comprehensive guide delves into the process of determining the LCM of 105 and 770, explaining multiple approaches and providing a deeper understanding of the principles involved. We'll explore everything from the basic definition of LCM to advanced techniques, ensuring you'll grasp this concept thoroughly.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in number theory with applications in various fields, including fractions, scheduling problems, and music theory. For example, finding the LCM helps determine when two cyclical events will coincide.
Method 1: Prime Factorization Method
This is arguably the most fundamental and widely used method for finding the LCM. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of 105
Let's start by finding the prime factorization of 105. We can systematically divide 105 by prime numbers until we reach 1:
105 ÷ 3 = 35 35 ÷ 5 = 7 7 ÷ 7 = 1
Therefore, the prime factorization of 105 is 3 x 5 x 7.
Step 2: Prime Factorization of 770
Now, let's do the same for 770:
770 ÷ 2 = 385 385 ÷ 5 = 77 77 ÷ 7 = 11 11 ÷ 11 = 1
Therefore, the prime factorization of 770 is 2 x 5 x 7 x 11.
Step 3: Identifying Common and Unique Prime Factors
Compare the prime factorizations of 105 (3 x 5 x 7) and 770 (2 x 5 x 7 x 11). We identify the common prime factors and the unique prime factors:
- Common prime factors: 5 and 7
- Unique prime factors: 2, 3, and 11
Step 4: Calculating the LCM
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(105, 770) = 2 x 3 x 5 x 7 x 11 = 2310
Therefore, the least common multiple of 105 and 770 is 2310.
Method 2: Listing Multiples Method
This method is more intuitive for smaller numbers but becomes less efficient as the numbers increase. It involves listing the multiples of each number until you find the smallest multiple common to both.
Step 1: Listing Multiples of 105
Multiples of 105: 105, 210, 315, 420, 525, 630, 735, 840, 945, 1050, 1155, 1260, 1365, 1470, 1575, 1680, 1785, 1890, 2095, 2100, 2205, 2310...
Step 2: Listing Multiples of 770
Multiples of 770: 770, 1540, 2310...
Step 3: Identifying the Smallest Common Multiple
By comparing the lists, we see that the smallest multiple common to both 105 and 770 is 2310. Therefore, the LCM(105, 770) = 2310. This method, while straightforward, can be time-consuming for larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are related through a simple formula:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers. We can use this relationship to find the LCM if we know the GCD.
Step 1: Finding the GCD of 105 and 770 using the Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCD.
- Divide the larger number (770) by the smaller number (105): 770 ÷ 105 = 7 with a remainder of 35.
- Replace the larger number with the smaller number (105) and the smaller number with the remainder (35): 105 ÷ 35 = 3 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 35.
Therefore, GCD(105, 770) = 35.
Step 2: Calculating the LCM using the formula
Now, we can use the formula:
LCM(105, 770) = (105 x 770) / GCD(105, 770) = (105 x 770) / 35 = 2310
This method is efficient, especially for larger numbers, as finding the GCD is computationally less intensive than directly finding the LCM through other methods.
Understanding the Relationship between LCM and GCD
The relationship between the LCM and GCD is a fundamental concept in number theory. It highlights the interconnectedness of these two seemingly disparate ideas. The formula LCM(a, b) * GCD(a, b) = a * b provides a powerful tool for calculating one if the other is known. This relationship simplifies calculations significantly, especially when dealing with larger numbers where the prime factorization method might become cumbersome. Understanding this interdependency expands your mathematical toolkit and allows you to approach problems from multiple perspectives.
Applications of LCM in Real-World Scenarios
While the LCM might seem like an abstract mathematical concept, it has numerous practical applications:
- Scheduling: Determining when events that occur at regular intervals will coincide. For example, if one event occurs every 105 days and another every 770 days, the LCM helps determine when they will both occur on the same day.
- Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions requires finding the LCM of the denominators.
- Music Theory: Determining the harmonic intervals between notes often involves understanding the LCM of the frequencies of the notes.
- Gear Ratios: In mechanical engineering, calculating gear ratios and understanding synchronization of rotating parts often requires LCM calculations.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
The Least Common Multiple (LCM) is the smallest number that is a multiple of both numbers. The Greatest Common Divisor (GCD) is the largest number that divides both numbers without leaving a remainder.
Q2: Can I use a calculator to find the LCM?
Yes, many scientific calculators have a built-in function to calculate the LCM of two or more numbers. However, understanding the underlying methods is crucial for developing a strong mathematical foundation.
Q3: Why is the prime factorization method important?
The prime factorization method provides a systematic and fundamental approach to finding the LCM. It reinforces the understanding of prime numbers and their role in number theory. It's also a versatile method applicable to a wide range of numbers.
Q4: Is there only one LCM for any two given numbers?
Yes, there is only one least common multiple for any pair of integers.
Q5: What if the two numbers are relatively prime (their GCD is 1)?
If the GCD of two numbers is 1 (meaning they share no common factors other than 1), then their LCM is simply the product of the two numbers.
Conclusion
Finding the LCM of 105 and 770, as demonstrated through various methods, is not merely about obtaining the answer (2310). It's about understanding the fundamental principles of number theory, mastering different calculation techniques, and appreciating the interconnectedness of mathematical concepts. The prime factorization method provides a foundational understanding, while the GCD method offers efficiency, particularly for larger numbers. The ability to solve such problems efficiently and understand their applications in real-world scenarios showcases a strong grasp of mathematical reasoning. The knowledge gained from this comprehensive exploration extends far beyond simply finding the LCM of two specific numbers, laying the groundwork for tackling more complex mathematical problems in the future.
Latest Posts
Latest Posts
-
Negative Words Beginning With A
Sep 12, 2025
-
Square Feet To Cubic Meter
Sep 12, 2025
-
How Far Is 2 5 Kilometers
Sep 12, 2025
-
Convert 39 Inches To Cm
Sep 12, 2025
-
What Is 1 3 In Percentage
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 105 And 770 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.