Lcm Of 110 And 231
elan
Sep 13, 2025 · 6 min read
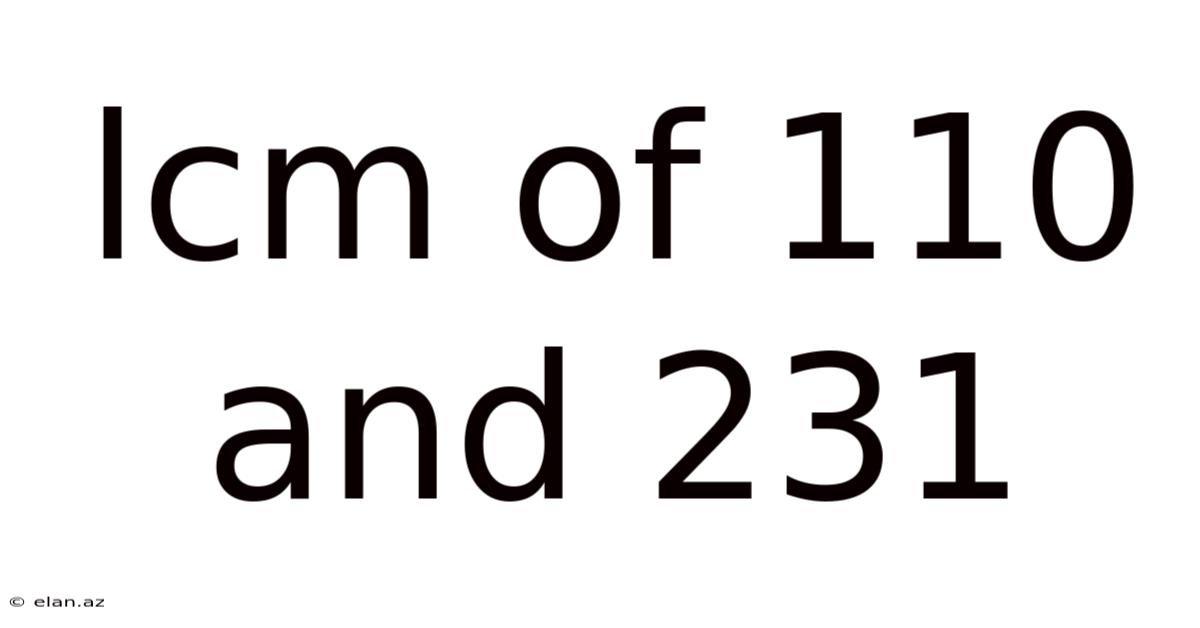
Table of Contents
Finding the Least Common Multiple (LCM) of 110 and 231: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and different methods involved can significantly enhance your mathematical comprehension. This article delves into the process of calculating the LCM of 110 and 231, exploring various approaches and providing a detailed explanation along the way. We'll move beyond simple calculation and uncover the theoretical foundations that underpin this crucial concept in number theory. This will equip you with the tools to tackle similar problems with confidence and a deeper understanding.
Understanding Least Common Multiple (LCM)
Before we dive into the calculation, let's solidify our understanding of the LCM. The least common multiple of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that both (or all) of the original numbers can divide into evenly. This concept is fundamental in various mathematical applications, from simplifying fractions to solving problems involving cycles and periodic events.
For example, the multiples of 4 are 4, 8, 12, 16, 20, 24, and so on. The multiples of 6 are 6, 12, 18, 24, 30, and so on. The common multiples of 4 and 6 are 12, 24, 36, etc. The least common multiple is 12.
Method 1: Prime Factorization
This method is widely considered the most efficient and insightful way to find the LCM of larger numbers, especially when dealing with more than two numbers. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors).
Steps:
-
Find the prime factorization of each number:
- 110 = 2 x 5 x 11
- 231 = 3 x 7 x 11
-
Identify the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, 5, 7, and 11.
- The highest power of 2 is 2¹
- The highest power of 3 is 3¹
- The highest power of 5 is 5¹
- The highest power of 7 is 7¹
- The highest power of 11 is 11¹
-
Multiply the highest powers together:
LCM(110, 231) = 2¹ x 3¹ x 5¹ x 7¹ x 11¹ = 2 x 3 x 5 x 7 x 11 = 2310
Therefore, the least common multiple of 110 and 231 is 2310. This means 2310 is the smallest positive integer that is divisible by both 110 and 231.
Method 2: Listing Multiples
This method is straightforward but can become cumbersome for larger numbers. It involves listing the multiples of each number until a common multiple is found.
Steps:
-
List the multiples of 110: 110, 220, 330, 440, 550, 660, 770, 880, 990, 1100, 1210, 1320, 1430, 1540, 1650, 1760, 1870, 1980, 2090, 2200, 2310,...
-
List the multiples of 231: 231, 462, 693, 924, 1155, 1386, 1617, 1848, 2079, 2310,...
-
Identify the smallest common multiple: The smallest number that appears in both lists is 2310.
Therefore, the LCM(110, 231) = 2310. While this method works, it's less efficient than prime factorization, especially when dealing with larger numbers or finding the LCM of more than two numbers.
Method 3: Using the Formula LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder.
Steps:
-
Find the GCD of 110 and 231 using the Euclidean algorithm:
- Divide 231 by 110: 231 = 2 x 110 + 11
- Divide 110 by 11: 110 = 10 x 11 + 0
The last non-zero remainder is the GCD, which is 11.
-
Apply the formula:
LCM(110, 231) = (110 x 231) / 11 = 25410 / 11 = 2310
This method is efficient for relatively small numbers. However, finding the GCD for very large numbers can still be computationally intensive.
A Deeper Dive: The Relationship Between LCM and GCD
The formula used in Method 3 highlights a fundamental relationship between the LCM and GCD of two integers, a and b:
LCM(a, b) x GCD(a, b) = a x b
This equation provides a powerful connection between these two crucial concepts in number theory. Understanding this relationship allows for a more holistic understanding of the divisibility properties of integers.
Applications of LCM
The concept of LCM has wide-ranging applications across various fields:
- Scheduling: Determining when events will occur simultaneously (e.g., two buses arriving at the same stop at the same time).
- Fractions: Finding the least common denominator when adding or subtracting fractions.
- Cyclic Processes: Analyzing repeating patterns or cycles in various systems.
- Music Theory: Determining the intervals between musical notes and harmonies.
- Computer Science: Synchronization of processes and tasks.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
- A: The LCM (Least Common Multiple) is the smallest positive integer that is a multiple of both numbers, while the GCD (Greatest Common Divisor) is the largest positive integer that divides both numbers without leaving a remainder.
-
Q: Can the LCM of two numbers be smaller than the larger of the two numbers?
- A: Yes, this can happen if one number is a multiple of the other. For example, LCM(6, 12) = 12.
-
Q: Is there a way to find the LCM of more than two numbers?
- A: Yes, the prime factorization method extends readily to finding the LCM of any number of integers. You find the prime factorization of each number, identify the highest power of each prime factor present, and multiply these highest powers together.
-
Q: What if the two numbers are relatively prime (their GCD is 1)?
- A: If the GCD of two numbers is 1, then their LCM is simply the product of the two numbers. This is because they share no common factors other than 1.
Conclusion
Finding the LCM of 110 and 231, as demonstrated, highlights the importance of understanding both the procedural aspects and the theoretical underpinnings of this mathematical concept. The prime factorization method stands out as the most efficient and conceptually clarifying approach, especially for larger numbers or multiple numbers. Understanding the relationship between the LCM and GCD further strengthens your mathematical toolkit, opening doors to a deeper appreciation of number theory and its diverse applications in various fields. Remember, mastering these concepts is not just about obtaining an answer; it's about cultivating a deeper understanding of the fundamental principles governing the behavior of numbers.
Latest Posts
Latest Posts
-
The Normal To The Curve
Sep 13, 2025
-
Triangular Numbers Up To 100
Sep 13, 2025
-
What Is A Radiant Heat
Sep 13, 2025
-
Words That Rhymes With That
Sep 13, 2025
-
What Metal Is The Lightest
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 110 And 231 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.