Lcm Of 12 15 10
elan
Sep 13, 2025 · 6 min read
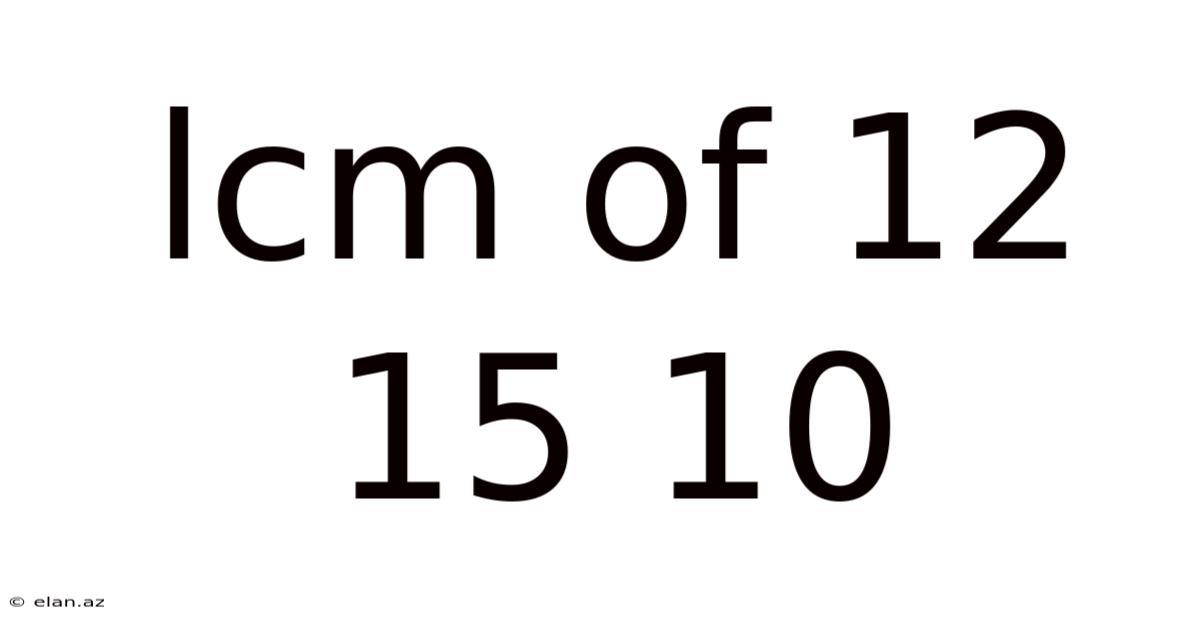
Table of Contents
Finding the Least Common Multiple (LCM) of 12, 15, and 10: A Comprehensive Guide
Finding the Least Common Multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial for a strong foundation in mathematics. This comprehensive guide will explore various approaches to finding the LCM of 12, 15, and 10, delving into the theoretical underpinnings and practical applications. We will move beyond a simple answer and equip you with the knowledge to tackle similar problems with confidence.
Introduction: Understanding LCM
The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is a multiple of all the numbers. Think of it as the smallest number that all the given numbers can divide into evenly. Understanding LCM is fundamental in many areas, including:
- Fraction Operations: Finding a common denominator when adding or subtracting fractions.
- Scheduling Problems: Determining when events will occur simultaneously (e.g., buses arriving at a stop).
- Measurement Conversions: Finding a common unit for different measurements.
- Abstract Algebra: Understanding concepts related to modular arithmetic and group theory.
Let's focus on finding the LCM of 12, 15, and 10. We'll explore several methods, starting with the most intuitive and progressing to more efficient techniques.
Method 1: Listing Multiples
The simplest, albeit often the least efficient method, involves listing the multiples of each number until a common multiple is found.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120...
By comparing the lists, we can see that the smallest number common to all three lists is 60. Therefore, the LCM(12, 15, 10) = 60. This method works well for smaller numbers, but it becomes increasingly cumbersome as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient and systematic, especially for larger numbers. It relies on expressing each number as a product of its prime factors. Prime factorization breaks a number down into its smallest prime number components.
- Prime Factorization of 12: 2 x 2 x 3 = 2² x 3¹
- Prime Factorization of 15: 3 x 5 = 3¹ x 5¹
- Prime Factorization of 10: 2 x 5 = 2¹ x 5¹
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Multiply these highest powers together: 4 x 3 x 5 = 60. Therefore, the LCM(12, 15, 10) = 60. This method is far more efficient than listing multiples, especially when dealing with larger numbers.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula connecting them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, although the calculation becomes slightly more complex. Let's first find the GCD of 12, 15, and 10 using the Euclidean algorithm (a method for finding the greatest common divisor of two integers):
-
GCD(12, 15):
- 15 = 12 x 1 + 3
- 12 = 3 x 4 + 0
- The GCD(12, 15) = 3
-
GCD(3, 10):
- 10 = 3 x 3 + 1
- 3 = 1 x 3 + 0
- The GCD(3, 10) = 1
Therefore, the GCD(12, 15, 10) = 1. Note that finding the GCD of more than two numbers involves finding the GCD iteratively.
Now, we can use the relationship between LCM and GCD. However, extending the formula directly to three numbers requires careful consideration and is less straightforward. The prime factorization method is generally preferred for more than two numbers. In this case, knowing the GCD helps understand the relative simplicity of the LCM calculation.
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method stands out as the most robust and efficient method for finding the LCM, especially when dealing with larger numbers or more than two numbers. Understanding why it works involves exploring the fundamental theorem of arithmetic.
The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors). This uniqueness is critical. It means that each number has a distinct prime factorization, like a unique fingerprint.
When finding the LCM using prime factorization, we are essentially constructing the "smallest" number that contains all the prime factors of the given numbers with at least the highest powers observed among them. This ensures that all the original numbers divide evenly into the resulting LCM. This method avoids the trial-and-error nature of listing multiples, providing a systematic and reliable way to compute the LCM.
Real-World Applications of LCM
The seemingly abstract concept of LCM finds practical applications in various real-world scenarios:
- Scheduling: Imagine three buses that arrive at a bus stop at intervals of 12, 15, and 10 minutes, respectively. Finding the LCM (60 minutes) tells you when all three buses will arrive simultaneously again.
- Fraction Arithmetic: When adding fractions with different denominators, finding the LCM of the denominators allows you to express the fractions with a common denominator, simplifying the addition or subtraction process.
- Project Management: If tasks in a project take 12, 15, and 10 hours respectively, finding the LCM can help in scheduling to minimize idle time.
- Construction: Cutting materials of different lengths efficiently requires understanding LCM to minimize waste.
Frequently Asked Questions (FAQ)
Q: What if the numbers have no common factors?
A: If the numbers are coprime (meaning their greatest common divisor is 1), the LCM is simply the product of the numbers. For example, the LCM of 7 and 11 (coprime numbers) is 77 (7 x 11).
Q: Can I use a calculator to find the LCM?
A: Many scientific calculators and online calculators have built-in functions to compute the LCM of numbers. However, understanding the underlying methods is crucial for problem-solving and developing a strong mathematical foundation.
Q: Is there a formula for finding the LCM of more than two numbers?
A: While there isn't a single, simple formula like the one relating LCM and GCD for two numbers, the prime factorization method extends effectively to any number of integers. You find the prime factorization of each number, then take the highest power of each prime factor that appears in any of the factorizations, and multiply them together.
Q: Why is prime factorization so important in mathematics?
A: Prime factorization is a fundamental concept in number theory with wide-ranging applications. It's essential for understanding concepts like modular arithmetic, cryptography, and various aspects of abstract algebra. Its importance stems from the unique representation of every integer greater than 1 as a product of primes.
Conclusion
Finding the LCM of 12, 15, and 10, while seemingly straightforward, offers a window into essential mathematical concepts. We've explored different methods, emphasizing the prime factorization method for its efficiency and theoretical significance. Understanding LCM is not just about solving a specific problem; it's about grasping fundamental principles that underpin more advanced mathematical concepts and find practical applications in a variety of fields. By mastering this seemingly simple concept, you build a stronger foundation for more complex mathematical challenges and real-world problem-solving. Remember, the key is not just to find the answer (which is 60) but to understand why that answer is correct and how to approach similar problems with confidence.
Latest Posts
Latest Posts
-
Is Megabyte Bigger Than Kb
Sep 13, 2025
-
Words That Rhyme With Like
Sep 13, 2025
-
Urdu Numbers 1 To 10
Sep 13, 2025
-
Example Of A Displacement Reaction
Sep 13, 2025
-
Convert Metres To Sq Metres
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 15 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.