Lcm Of 15 And 9
elan
Sep 14, 2025 · 6 min read
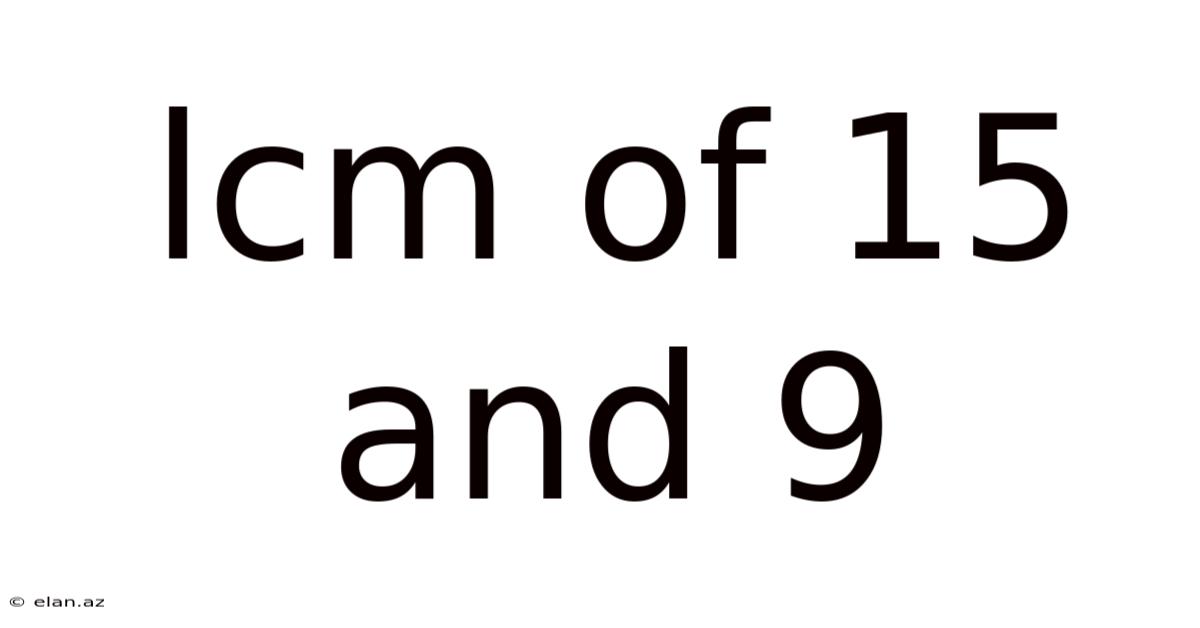
Table of Contents
Unveiling the Least Common Multiple (LCM) of 15 and 9: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles reveals a fascinating glimpse into number theory. This article will delve into the intricacies of calculating the LCM of 15 and 9, exploring various methods and demonstrating their applications beyond basic arithmetic. We'll cover different approaches, explain the theoretical foundation, and address common questions, making this a comprehensive guide for anyone seeking a deeper understanding of LCMs.
Introduction: Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding LCMs is crucial in various mathematical applications, from simplifying fractions to solving problems involving cyclical events. This article focuses on finding the LCM of 15 and 9, using this specific example to illustrate broader concepts applicable to any pair of integers.
Method 1: Listing Multiples
One straightforward method to find the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this to 15 and 9:
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99...
By comparing the lists, we observe that the smallest common multiple is 45. Therefore, the LCM of 15 and 9 is 45. This method is effective for smaller numbers, but it becomes less practical when dealing with larger numbers where listing multiples can be time-consuming.
Method 2: Prime Factorization
A more efficient and elegant approach involves using prime factorization. This method is particularly useful when dealing with larger numbers. Prime factorization breaks down a number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 15: 3 x 5
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization:
- Identify all prime factors: In this case, we have 3 and 5.
- Find the highest power of each prime factor: The highest power of 3 is 3² (from the factorization of 9), and the highest power of 5 is 5¹ (from the factorization of 15).
- Multiply the highest powers together: 3² x 5 = 9 x 5 = 45
Therefore, the LCM of 15 and 9 is 45, confirming the result obtained using the listing method. This method is significantly more efficient for larger numbers because it avoids the tedious process of listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are intimately related. The GCD is the largest number that divides both integers without leaving a remainder. There's a handy formula connecting the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Let's use this formula to find the LCM of 15 and 9:
-
Find the GCD of 15 and 9: The factors of 15 are 1, 3, 5, and 15. The factors of 9 are 1, 3, and 9. The greatest common factor is 3. Therefore, GCD(15, 9) = 3.
-
Apply the formula: LCM(15, 9) x GCD(15, 9) = 15 x 9 LCM(15, 9) x 3 = 135 LCM(15, 9) = 135 / 3 = 45
Again, we arrive at the LCM of 45. This method highlights the interconnectedness of LCM and GCD, providing an alternative route to the solution. Finding the GCD can be done using the Euclidean algorithm, which is particularly efficient for larger numbers.
The Euclidean Algorithm for Finding GCD
The Euclidean algorithm is an efficient method for finding the greatest common divisor (GCD) of two integers. It's based on the principle that the GCD of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCD.
Let's illustrate with 15 and 9:
- 15 = 1 x 9 + 6 (The remainder is 6)
- 9 = 1 x 6 + 3 (The remainder is 3)
- 6 = 2 x 3 + 0 (The remainder is 0)
The last non-zero remainder is 3, which is the GCD(15, 9). This algorithm is far more efficient than listing factors for larger numbers.
Applications of LCM in Real-World Scenarios
The concept of LCM extends beyond abstract mathematical exercises. It finds practical application in various real-world scenarios:
-
Scheduling: Imagine two buses depart from a station at different intervals. One bus departs every 15 minutes, and another every 9 minutes. The LCM (45 minutes) determines when both buses will depart simultaneously again.
-
Fraction addition and subtraction: Finding a common denominator when adding or subtracting fractions involves determining the LCM of the denominators.
-
Cyclic processes: In physics and engineering, cyclical processes, such as the rotation of gears or the oscillation of pendulums, can be analyzed using LCM to determine when events coincide.
-
Project planning: In project management, the LCM can be used to synchronize tasks with different durations.
-
Pattern recognition: LCM is useful in identifying recurring patterns or cycles in data analysis.
Frequently Asked Questions (FAQ)
Q1: What if the two numbers are relatively prime (their GCD is 1)?
If the GCD of two numbers is 1, meaning they share no common factors other than 1, then their LCM is simply the product of the two numbers. For example, the LCM of 7 and 11 (relatively prime) is 77 (7 x 11).
Q2: Can the LCM be larger than the product of the two numbers?
No, the LCM of two numbers is always less than or equal to their product. This stems from the relationship between LCM and GCD mentioned earlier.
Q3: How do I find the LCM of more than two numbers?
To find the LCM of more than two numbers, you can extend the prime factorization method. Find the prime factorization of each number, identify the highest power of each prime factor present, and multiply those highest powers together. Alternatively, you can find the LCM of the first two numbers, then find the LCM of that result and the third number, and so on.
Conclusion: Mastering the LCM
Finding the least common multiple is a fundamental concept in number theory with practical applications across various fields. While simple listing works for smaller numbers, the prime factorization method offers a more efficient and generalizable approach, especially when dealing with larger numbers. The relationship between LCM and GCD further enhances our understanding and provides alternative calculation methods. Mastering these techniques allows for a deeper appreciation of mathematical principles and their real-world relevance. This comprehensive exploration of finding the LCM of 15 and 9 provides a solid foundation for tackling more complex problems involving least common multiples. Remember to choose the method best suited to the problem at hand, balancing efficiency and understanding.
Latest Posts
Latest Posts
-
5 Letter Word Beginning Sa
Sep 14, 2025
-
How Do I Spell 3
Sep 14, 2025
-
How To Draw An Angle
Sep 14, 2025
-
Words That End With Ail
Sep 14, 2025
-
Whats 36 Inches In Cm
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 15 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.