Lcm Of 18 And 12
elan
Sep 14, 2025 · 5 min read
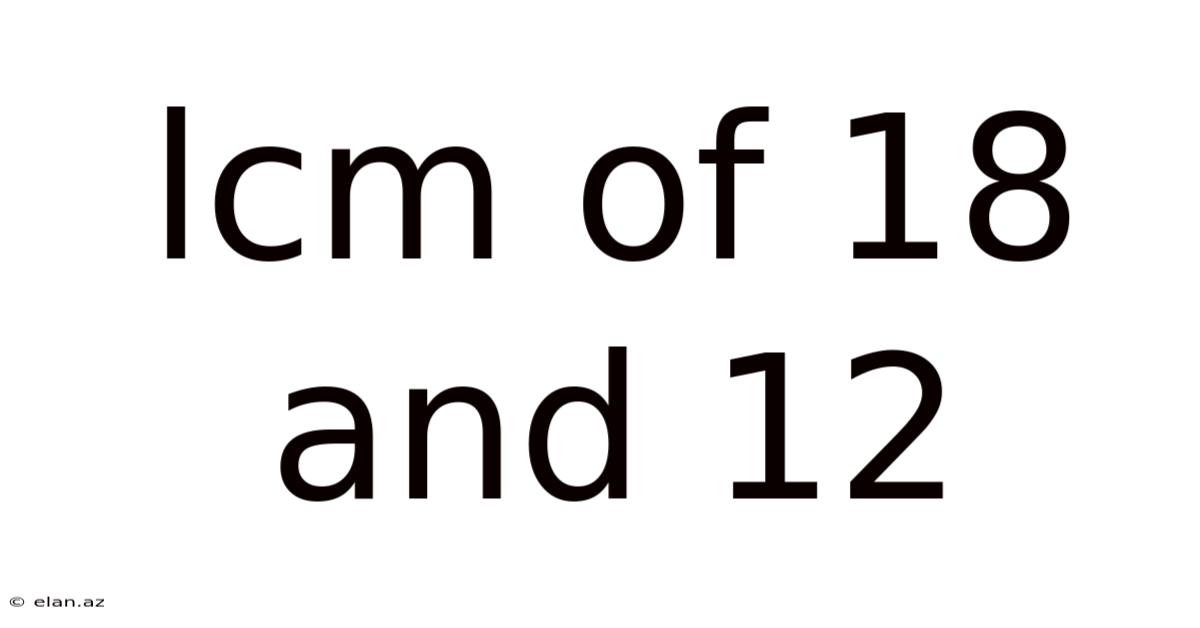
Table of Contents
Finding the Least Common Multiple (LCM) of 18 and 12: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers, like 18 and 12, is a fundamental concept in mathematics with applications across various fields, from scheduling tasks to understanding fractions and ratios. This comprehensive guide will walk you through multiple methods of calculating the LCM of 18 and 12, explaining the underlying principles and providing practical examples. We'll also delve into the theoretical background to ensure a thorough understanding. By the end, you'll not only know the LCM of 18 and 12 but also possess the skills to calculate the LCM of any two numbers.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's define the term. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, if we consider the numbers 2 and 3, their LCM is 6 because 6 is the smallest number divisible by both 2 and 3.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 18 and 12. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, ...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, ...
By comparing the lists, we can see that the smallest number that appears in both lists is 36. Therefore, the LCM of 18 and 12 is 36. This method is simple to visualize but becomes less efficient with larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
Step 1: Find the prime factorization of each number.
- Prime factorization of 18: 2 × 3² (18 = 2 x 9 = 2 x 3 x 3)
- Prime factorization of 12: 2² × 3 (12 = 2 x 6 = 2 x 2 x 3)
Step 2: Identify the highest power of each prime factor present in either factorization.
In our example, the prime factors are 2 and 3.
- The highest power of 2 is 2² = 4.
- The highest power of 3 is 3² = 9.
Step 3: Multiply the highest powers together.
LCM(18, 12) = 2² × 3² = 4 × 9 = 36
Therefore, the LCM of 18 and 12 is 36 using the prime factorization method. This method is generally preferred for its efficiency and clarity, especially when dealing with larger numbers or multiple numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. There's a formula that links them:
LCM(a, b) = (|a × b|) / GCD(a, b)
where:
- a and b are the two numbers.
- |a × b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
Step 1: Find the GCD of 18 and 12.
We can use the Euclidean algorithm to find the GCD.
- 18 = 12 × 1 + 6
- 12 = 6 × 2 + 0
The last non-zero remainder is 6, so GCD(18, 12) = 6.
Step 2: Apply the formula.
LCM(18, 12) = (18 × 12) / 6 = 216 / 6 = 36
Therefore, the LCM of 18 and 12 is 36 using the GCD method. This method is particularly useful when you already know the GCD of the numbers.
Visual Representation: Venn Diagram
A Venn diagram can provide a visual understanding of the LCM and GCD. Represent the prime factors of each number in separate circles, with overlapping sections representing common factors.
18 (2 x 3 x 3) 12 (2 x 2 x 3)
/ \ / \
/ \ / \
2 3 x 3 2 x 2 3
| | | |
| | | |
GCD = 2 x 3 = 6 LCM = 2 x 2 x 3 x 3 = 36
The overlapping section contains the common factors, which constitute the GCD (6). The LCM is obtained by multiplying all unique prime factors with their highest powers.
Applications of LCM
The LCM has numerous applications across various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if one event happens every 12 hours and another every 18 hours, they will coincide every 36 hours (the LCM of 12 and 18).
-
Fractions: Finding the least common denominator when adding or subtracting fractions. To add 1/12 and 1/18, the LCM of 12 and 18 (36) is used as the common denominator.
-
Cycles and Patterns: Identifying when cyclical events repeat simultaneously. This is relevant in various areas like physics, engineering, and computer science.
-
Modular Arithmetic: Used extensively in cryptography and other areas of number theory.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest multiple common to both numbers, while the GCD is the largest factor common to both numbers. They are inversely related.
-
Can the LCM of two numbers be larger than their product? No, the LCM of two numbers is always less than or equal to the product of the two numbers.
-
What if one of the numbers is 0? The LCM of any number and 0 is undefined.
-
How do I find the LCM of more than two numbers? Extend the prime factorization method: find the prime factorization of all numbers, identify the highest power of each prime factor present in any factorization, and multiply them together. The GCD method can also be extended using a recursive approach.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with widespread practical applications. While the method of listing multiples works well for smaller numbers, prime factorization provides a more efficient and insightful approach for larger numbers. Understanding the relationship between the LCM and GCD further enhances our ability to solve problems involving these concepts. Remember, the key lies in breaking down the numbers into their prime factors and then strategically combining them to find the LCM. This comprehensive guide has equipped you with the knowledge and methods to confidently tackle any LCM calculation, regardless of the numbers involved.
Latest Posts
Latest Posts
-
Describing Words Beginning With T
Sep 14, 2025
-
Hcf Of 70 And 110
Sep 14, 2025
-
Commutator In An Electric Motor
Sep 14, 2025
-
Words That End In Ous
Sep 14, 2025
-
Symbol Of Silver And Gold
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 18 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.