Lcm Of 20 And 35
elan
Sep 21, 2025 · 5 min read
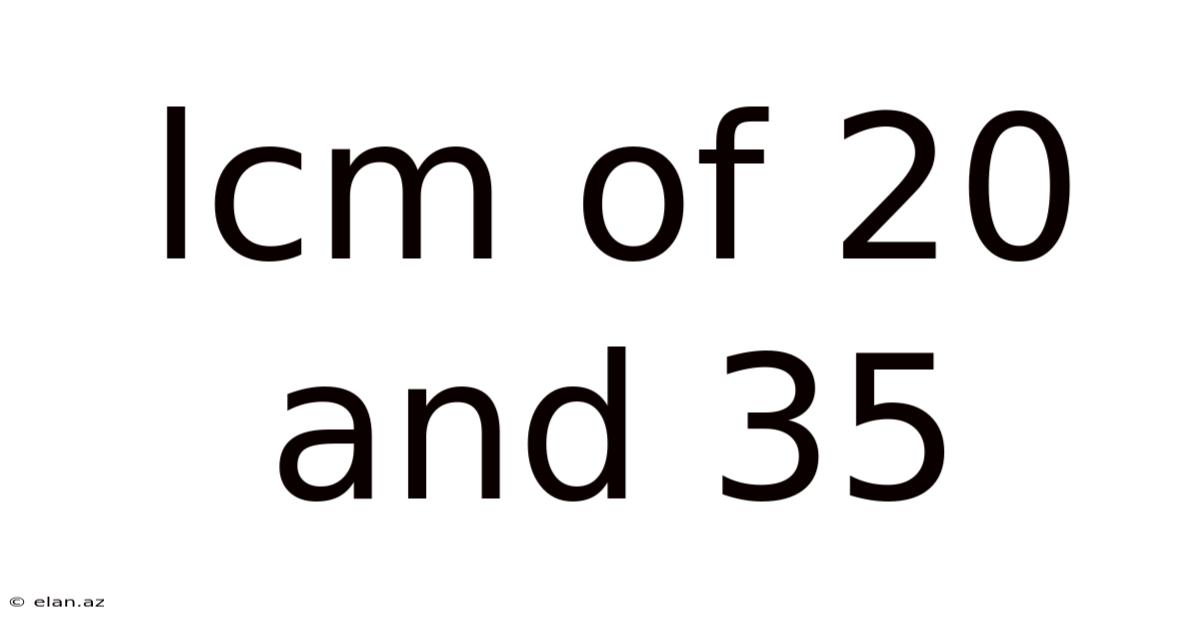
Table of Contents
Finding the Least Common Multiple (LCM) of 20 and 35: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple mathematical task, but understanding the underlying concepts and different methods for calculating it can significantly improve your mathematical problem-solving skills. This article delves into the LCM of 20 and 35, exploring various approaches, explaining the reasoning behind each step, and providing a solid foundation for tackling more complex LCM problems. We'll cover prime factorization, listing multiples, and using the greatest common divisor (GCD). By the end, you'll not only know the LCM of 20 and 35 but also possess a broader understanding of LCM calculations.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. Understanding the LCM is crucial in various mathematical applications, from solving fraction problems to scheduling events that occur at regular intervals.
Method 1: Prime Factorization
This method is arguably the most efficient way to find the LCM of larger numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
1. Find the Prime Factorization of 20:
20 can be broken down as follows:
- 20 = 2 x 10
- 10 = 2 x 5
Therefore, the prime factorization of 20 is 2² x 5.
2. Find the Prime Factorization of 35:
35 can be broken down as follows:
- 35 = 5 x 7
Therefore, the prime factorization of 35 is 5 x 7.
3. Identify the Highest Power of Each Prime Factor:
Looking at both factorizations (2² x 5 and 5 x 7), we identify the highest power of each prime factor present:
- The highest power of 2 is 2².
- The highest power of 5 is 5¹ (since 5 appears in both).
- The highest power of 7 is 7¹.
4. Multiply the Highest Powers Together:
To find the LCM, multiply the highest powers of each prime factor together:
LCM(20, 35) = 2² x 5 x 7 = 4 x 5 x 7 = 140
Therefore, the least common multiple of 20 and 35 is 140.
Method 2: Listing Multiples
This method is more intuitive but can be less efficient for larger numbers. It involves listing the multiples of each number until you find the smallest multiple that is common to both.
1. List Multiples of 20:
20, 40, 60, 80, 100, 120, 140, 160, 180, 200...
2. List Multiples of 35:
35, 70, 105, 140, 175, 210...
3. Identify the Smallest Common Multiple:
By comparing the lists, we can see that the smallest multiple common to both 20 and 35 is 140.
Therefore, the LCM(20, 35) = 140. This method is straightforward but becomes cumbersome with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
This method leverages the relationship between the LCM and the greatest common divisor (GCD). The GCD is the largest number that divides both numbers without leaving a remainder. The formula connecting LCM and GCD is:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
1. Find the GCD of 20 and 35:
We can use the Euclidean algorithm to find the GCD:
- Divide the larger number (35) by the smaller number (20): 35 = 20 x 1 + 15
- Replace the larger number with the remainder (15) and repeat: 20 = 15 x 1 + 5
- Repeat again: 15 = 5 x 3 + 0
The last non-zero remainder is the GCD, which is 5.
2. Apply the Formula:
Now, use the formula:
LCM(20, 35) = (20 x 35) / 5 = 700 / 5 = 140
Therefore, the LCM(20, 35) = 140. This method is efficient, especially for larger numbers, once you're comfortable with finding the GCD.
Why is the LCM Important?
Understanding the LCM extends beyond simple number theory. It has practical applications in various fields:
-
Fraction Arithmetic: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows you to find a common denominator, making the calculation easier.
-
Scheduling: Imagine two events occurring at regular intervals. The LCM helps determine when both events will occur simultaneously. For example, if Event A happens every 20 days and Event B happens every 35 days, they will coincide every 140 days (the LCM of 20 and 35).
-
Pattern Recognition: In various mathematical and scientific contexts, identifying repeating patterns relies on understanding multiples and common multiples, which directly relates to the LCM.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers. The GCD (Greatest Common Divisor) is the largest number that divides both numbers without leaving a remainder. They are inversely related; as the GCD increases, the LCM decreases, and vice versa.
Q: Can the LCM of two numbers be one of the numbers?
A: Yes, if one number is a multiple of the other. For example, the LCM of 10 and 20 is 20.
Q: What if I have more than two numbers? How do I find the LCM?
A: You can extend the prime factorization method to find the LCM of more than two numbers. Find the prime factorization of each number, identify the highest power of each prime factor present across all factorizations, and then multiply these highest powers together. The listing multiples method becomes significantly less efficient with more numbers.
Conclusion
Finding the LCM of 20 and 35, as demonstrated through various methods, highlights the importance of understanding fundamental mathematical concepts. Whether you utilize prime factorization, the listing multiples approach, or the GCD-based method, the result remains consistent: the LCM of 20 and 35 is 140. Mastering these techniques will equip you to tackle more complex LCM problems and appreciate the practical applications of this vital mathematical concept in diverse fields. Remember to choose the method most comfortable and efficient for you, depending on the numbers involved in the problem. The understanding of the underlying principles is key to successful problem-solving.
Latest Posts
Latest Posts
-
Function Of A Nuclear Pore
Sep 21, 2025
-
What Is Cl In Ml
Sep 21, 2025
-
80 000 Rupees In Pounds
Sep 21, 2025
-
Rugged Cliffs Crossword Puzzle Clue
Sep 21, 2025
-
Words That Contain A E
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 20 And 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.