Lcm Of 228 And 380
elan
Sep 16, 2025 · 6 min read
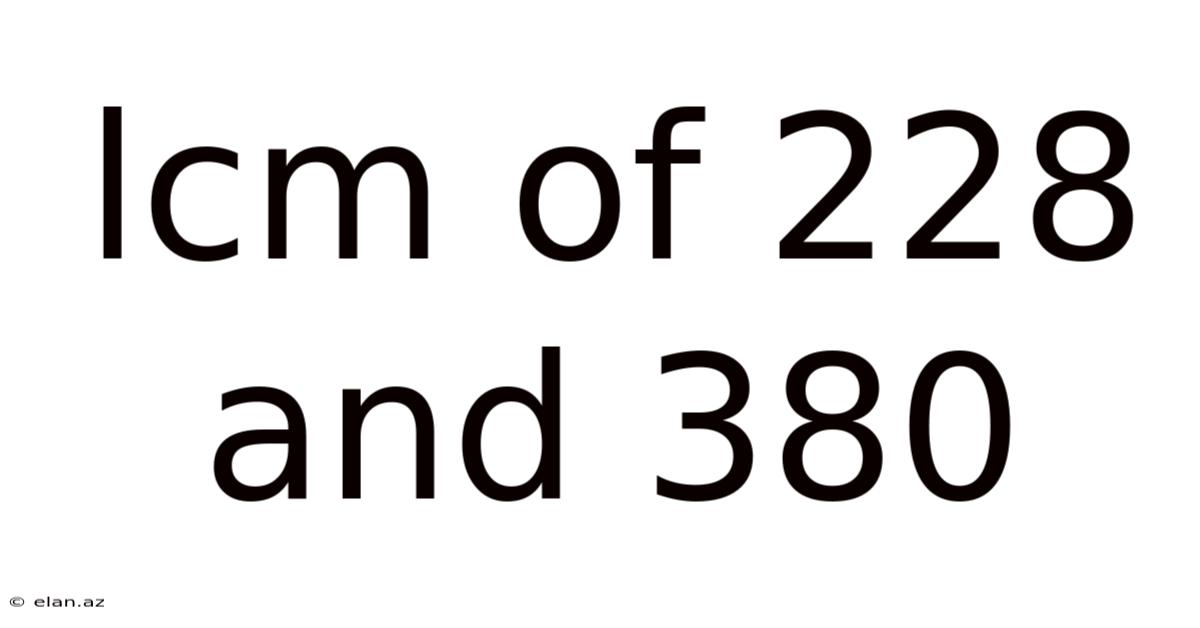
Table of Contents
Finding the Least Common Multiple (LCM) of 228 and 380: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial for a strong foundation in mathematics. This article delves into the calculation of the LCM of 228 and 380, exploring multiple approaches and highlighting the practical applications of this fundamental concept. We'll go beyond simply finding the answer and explore the "why" behind the methods, making this a valuable resource for students and anyone looking to refresh their understanding of LCM.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 228 and 380, let's clarify what LCM actually means. The least common multiple of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding this definition is key to grasping the different methods we'll use.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10... and the multiples of 3 are 3, 6, 9, 12... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
One straightforward method, suitable for smaller numbers, is to list the multiples of each number until you find the smallest common multiple. Let's try this for 228 and 380.
- Multiples of 228: 228, 456, 684, 912, 1140, 1368, 1596, 1824, 2052, 2280, ...
- Multiples of 380: 380, 760, 1140, 1520, 1900, 2280, ...
Notice that 1140 appears in both lists, but 2280 is also a common multiple. However, since we are looking for the least common multiple, 1140 is our answer using this method. This method is simple but becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient and widely applicable method involves prime factorization. This method breaks down each number into its prime factors—numbers divisible only by 1 and themselves.
Step 1: Prime Factorize 228
228 = 2 x 114 = 2 x 2 x 57 = 2 x 2 x 3 x 19 = 2² x 3 x 19
Step 2: Prime Factorize 380
380 = 2 x 190 = 2 x 2 x 95 = 2 x 2 x 5 x 19 = 2² x 5 x 19
Step 3: Identify Common and Unique Prime Factors
Now, we compare the prime factorizations of 228 and 380:
- 228 = 2² x 3 x 19
- 380 = 2² x 5 x 19
We see that both numbers share the prime factors 2² and 19. The unique prime factors are 3 (from 228) and 5 (from 380).
Step 4: Calculate the LCM
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together:
LCM(228, 380) = 2² x 3 x 5 x 19 = 4 x 3 x 5 x 19 = 1140
Therefore, using prime factorization, the LCM of 228 and 380 is 1140. This method is significantly more efficient for larger numbers than the listing multiples method.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. There's a formula that connects them:
LCM(a, b) = (a x b) / GCD(a, b)
Where 'a' and 'b' are the two numbers.
Step 1: Find the GCD of 228 and 380
We can use the Euclidean algorithm to find the GCD. The Euclidean algorithm is an efficient method for finding the greatest common divisor of two integers.
- Divide 380 by 228: 380 = 1 x 228 + 152
- Divide 228 by 152: 228 = 1 x 152 + 76
- Divide 152 by 76: 152 = 2 x 76 + 0
The last non-zero remainder is the GCD, which is 76.
Step 2: Calculate the LCM
Now, we use the formula:
LCM(228, 380) = (228 x 380) / 76 = 86640 / 76 = 1140
Again, the LCM of 228 and 380 is 1140. This method demonstrates the elegant relationship between LCM and GCD.
The Importance of LCM in Real-World Applications
While finding the LCM might seem like an abstract mathematical exercise, it has several practical applications in various fields:
- Scheduling: Imagine two buses arrive at a bus stop at different intervals. The LCM helps determine when both buses will arrive simultaneously again.
- Fractions: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators.
- Project Management: Determining the least common time frame for completing tasks that need to be synchronized.
- Music Theory: Understanding rhythmic patterns and musical intervals often utilizes the concept of LCM.
- Engineering: Calculating synchronized cycles in machines or processes.
Understanding LCM is fundamental to solving problems in these and other areas.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
The LCM is the smallest number that is a multiple of both numbers, while the GCD is the largest number that is a divisor of both numbers. They are inversely related, as shown by the formula connecting them.
Q2: Can I use a calculator to find the LCM?
Many scientific calculators and online calculators have built-in functions to calculate the LCM of two or more numbers.
Q3: What if I have more than two numbers?
The methods described above, particularly prime factorization, can be extended to find the LCM of more than two numbers. You would prime factorize each number, then take the highest power of each prime factor present in any of the factorizations and multiply them together.
Q4: Why is prime factorization the most efficient method for larger numbers?
Prime factorization systematically breaks down numbers into their fundamental building blocks. This method avoids the potentially lengthy process of listing multiples, especially when dealing with larger numbers. The algorithm is efficient and scales well with increasing number size.
Conclusion
Finding the least common multiple of 228 and 380, as we've demonstrated, can be achieved through several methods: listing multiples, prime factorization, and using the GCD. While listing multiples is straightforward for smaller numbers, prime factorization and the GCD method are more efficient and scalable for larger numbers and provide a deeper understanding of the mathematical concepts involved. The LCM is a fundamental concept with widespread applications in various fields, making its understanding crucial for a solid mathematical foundation and problem-solving skills. Regardless of the method you choose, the LCM of 228 and 380 consistently comes out to be 1140. Understanding the "why" behind these calculations is just as important as knowing the "how." Mastering the LCM concept opens doors to a more comprehensive understanding of number theory and its practical applications.
Latest Posts
Latest Posts
-
How Do You Pronounce Omniscient
Sep 16, 2025
-
Capital City Quiz With Answers
Sep 16, 2025
-
How Far Is 3000 Meters
Sep 16, 2025
-
Multiple Choice Quiz With Answers
Sep 16, 2025
-
Words That Rhyme With Different
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 228 And 380 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.