Lcm Of 24 And 84
elan
Sep 14, 2025 · 6 min read
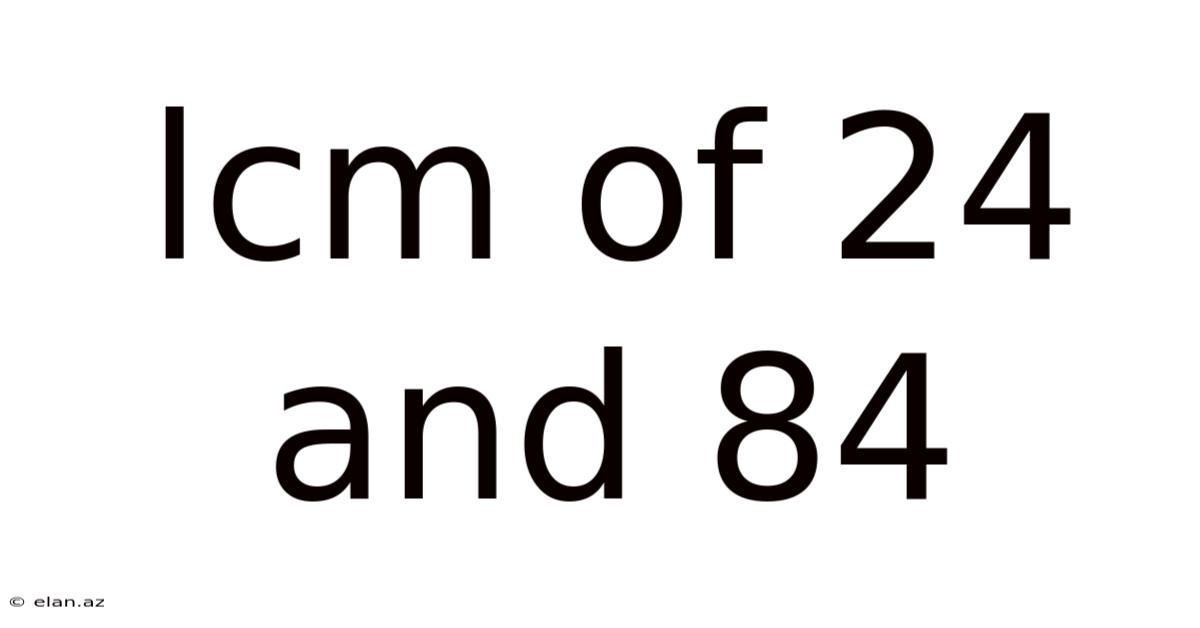
Table of Contents
Finding the Least Common Multiple (LCM) of 24 and 84: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can significantly enhance your mathematical proficiency. This comprehensive guide will delve into the process of calculating the LCM of 24 and 84, explaining multiple approaches, and exploring the broader implications of LCM in various mathematical contexts. We'll also address frequently asked questions to solidify your understanding.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers in your set as factors. Understanding LCM is crucial in various mathematical applications, from simplifying fractions to solving problems involving cycles and rhythms.
For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The common multiples of 2 and 3 are 6, 12, 18, 24, etc. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM of 24 and 84
Let's now tackle the LCM of 24 and 84 using several methods.
Method 1: Listing Multiples
This is the most straightforward method, particularly for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240...
- Multiples of 84: 84, 168, 252, 336...
By comparing the lists, we see that the smallest common multiple is 168. Therefore, the LCM(24, 84) = 168. However, this method becomes less efficient with larger numbers.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
-
Prime Factorization of 24:
24 = 2 × 12 = 2 × 2 × 6 = 2 × 2 × 2 × 3 = 2³ × 3¹
-
Prime Factorization of 84:
84 = 2 × 42 = 2 × 2 × 21 = 2 × 2 × 3 × 7 = 2² × 3¹ × 7¹
-
Constructing the LCM:
To find the LCM, we take the highest power of each prime factor present in the factorizations:
LCM(24, 84) = 2³ × 3¹ × 7¹ = 8 × 3 × 7 = 168
Therefore, the LCM of 24 and 84 is 168. This method is more systematic and less prone to errors, especially when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are related by the following formula:
LCM(a, b) × GCD(a, b) = a × b
Where 'a' and 'b' are the two numbers.
-
Finding the GCD of 24 and 84:
We can use the Euclidean algorithm to find the GCD:
84 = 3 × 24 + 12 24 = 2 × 12 + 0
The last non-zero remainder is the GCD, which is 12.
-
Calculating the LCM:
LCM(24, 84) = (24 × 84) / GCD(24, 84) = (24 × 84) / 12 = 168
This method is also efficient and relies on a well-established algorithm for finding the GCD.
Applications of LCM
The concept of LCM extends far beyond simple arithmetic exercises. It finds practical applications in various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if two buses leave a station at different intervals, the LCM helps determine when they will depart at the same time again.
-
Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
-
Modular Arithmetic: In cryptography and other areas of number theory, LCM plays a vital role in solving congruences.
-
Music Theory: Understanding rhythmic patterns and finding the least common denominator for different time signatures.
-
Construction and Engineering: Coordinating cyclical processes or timing events in projects requiring synchronized actions.
-
Computer Science: In algorithms and data structures, LCM is used in various optimization problems.
Elaboration on Prime Factorization Method
The prime factorization method offers a powerful and systematic way to find the LCM of any two or more numbers. Let's break down why it works:
Prime factorization expresses a number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be uniquely expressed as a product of prime numbers.
When we find the LCM using prime factorization, we are essentially building the smallest number that contains all the prime factors of both numbers, ensuring each factor appears with the highest power it has in either factorization. This guarantees that the resulting number is divisible by both original numbers and is the smallest such number.
For example, consider the LCM of 12 and 18:
- 12 = 2² × 3¹
- 18 = 2¹ × 3²
The LCM will be 2² × 3² = 4 × 9 = 36. Notice that 36 is divisible by both 12 and 18, and it's the smallest number with this property.
Frequently Asked Questions (FAQ)
Q: What if the two numbers have no common factors?
A: If the two numbers are relatively prime (i.e., their GCD is 1), then their LCM is simply their product. For example, LCM(5, 7) = 5 × 7 = 35.
Q: Can we find the LCM of more than two numbers?
A: Yes, the prime factorization method readily extends to finding the LCM of multiple numbers. You find the prime factorization of each number, and then the LCM is constructed by taking the highest power of each prime factor present in any of the factorizations.
Q: Why is the LCM important in fraction arithmetic?
A: When adding or subtracting fractions, we need a common denominator. The least common denominator (LCD) is the smallest denominator we can use, simplifying the calculations and the resulting fraction. The LCD is simply the LCM of the denominators of the fractions.
Q: Are there any limitations to the prime factorization method?
A: While efficient for most numbers, the prime factorization method can be computationally intensive for extremely large numbers where finding the prime factors becomes a challenge. For such cases, more advanced algorithms are used.
Q: How can I improve my understanding of LCM?
A: Practice is key! Try finding the LCM of various number pairs and sets using different methods. Work through examples and gradually increase the complexity of the numbers involved. Understanding the underlying concepts of prime factorization and the relationship between LCM and GCD is crucial for a deeper comprehension.
Conclusion
Finding the least common multiple is a fundamental concept in mathematics with far-reaching applications. Mastering different methods for calculating LCM, especially the prime factorization method, is essential for various mathematical tasks and problem-solving. This comprehensive guide not only provides a clear explanation of how to calculate the LCM of 24 and 84 but also equips you with a solid foundation to tackle LCM problems of increasing complexity and appreciate its significance in broader mathematical contexts. Remember that consistent practice and a thorough understanding of the underlying principles are key to mastering this important concept.
Latest Posts
Latest Posts
-
Polygons Exterior And Interior Angles
Sep 14, 2025
-
Thank You And Well Done
Sep 14, 2025
-
What Is Multiple Of 12
Sep 14, 2025
-
2 4 8 16 Pattern
Sep 14, 2025
-
What Are Subordinate Clauses Examples
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 24 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.