Lcm Of 3 And 8
elan
Sep 16, 2025 · 6 min read
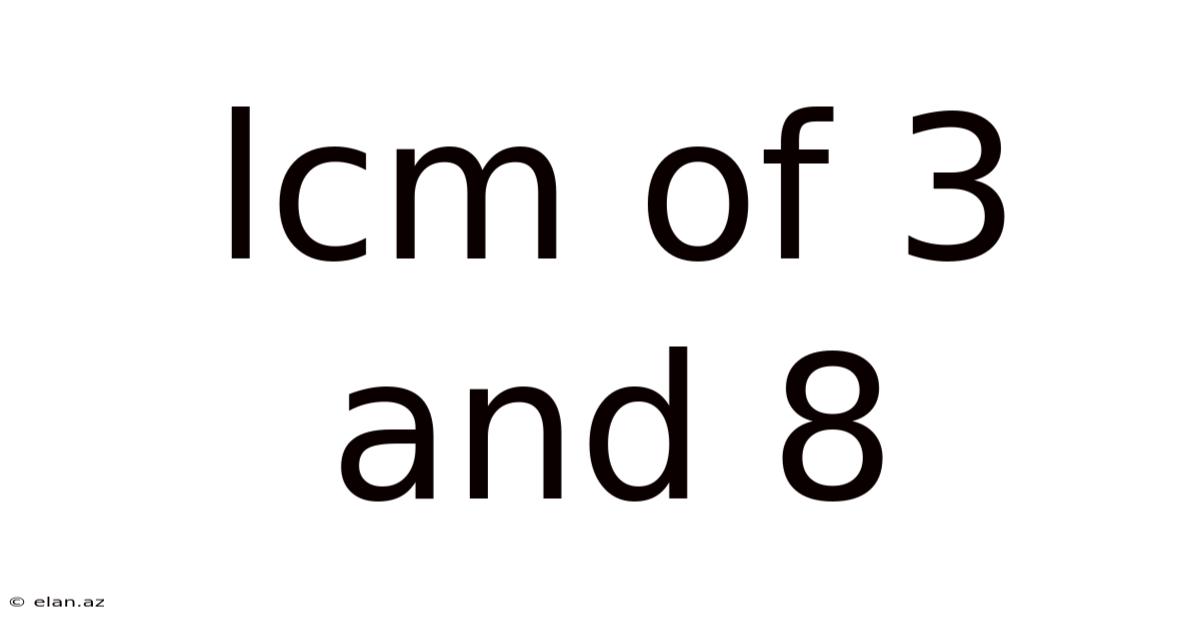
Table of Contents
Finding the Least Common Multiple (LCM) of 3 and 8: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it provides a strong foundation for more advanced mathematical concepts. This comprehensive guide will explore the LCM of 3 and 8, delving into various approaches, explaining the reasoning behind each step, and ultimately helping you grasp the broader significance of LCM in mathematics. We'll cover everything from basic definitions to practical applications, ensuring you have a complete understanding of this important topic.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. For example, if we're looking for the LCM of 2 and 3, the multiples of 2 are 2, 4, 6, 8, 10... and the multiples of 3 are 3, 6, 9, 12... The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6. In this article, we'll focus on finding the LCM of 3 and 8.
Method 1: Listing Multiples
This is the most straightforward approach, especially when dealing with smaller numbers like 3 and 8. Let's list the multiples of each number:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 8: 8, 16, 24, 32, 40...
By comparing the two lists, we can see that the smallest number common to both is 24. Therefore, the LCM of 3 and 8 is 24.
This method is simple and intuitive, but it becomes less efficient when dealing with larger numbers or a greater number of integers. Imagine trying to find the LCM of 12, 18, and 24 using this method – the list of multiples would become quite extensive.
Method 2: Prime Factorization
This method is more systematic and efficient, especially for larger numbers. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. Let's break down 3 and 8 into their prime factors:
- 3: The number 3 is a prime number itself, so its prime factorization is simply 3.
- 8: The prime factorization of 8 is 2 x 2 x 2 = 2³.
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The prime factor 2 appears only in the factorization of 8, with a power of 3 (2³).
- The prime factor 3 appears only in the factorization of 3, with a power of 1 (3¹).
Therefore, the LCM of 3 and 8 is 2³ x 3 = 8 x 3 = 24.
This method is far more efficient than listing multiples, especially when dealing with larger numbers. It's also easily scalable to find the LCM of more than two numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. There's a handy formula that connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
where:
- a and b are the two integers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
First, let's find the GCD of 3 and 8. Since 3 is a prime number and 8 is not divisible by 3, their GCD is 1.
Now, we can apply the formula:
LCM(3, 8) = (|3 x 8|) / GCD(3, 8) = 24 / 1 = 24
This method is particularly useful when dealing with larger numbers where finding the prime factorization might be more time-consuming. Algorithms for efficiently computing the GCD, like the Euclidean algorithm, make this method very efficient for large numbers.
Method 4: Visual Representation using Venn Diagrams
Venn diagrams can provide a visual representation of the relationship between the factors of two numbers and help in finding the LCM. Let's represent the prime factorization of 3 and 8 in a Venn diagram:
- 3: 3
- 8: 2 x 2 x 2
Since there are no common prime factors, the Venn diagram would show two separate circles, one for 3 and one for 2 x 2 x 2. To find the LCM, we multiply all the prime factors in both circles: 2 x 2 x 2 x 3 = 24.
While this method is visually intuitive for smaller numbers, it becomes less practical for larger numbers with more complex prime factorizations.
Explanation of the LCM in Mathematical Terms
The LCM is a fundamental concept in number theory and has numerous applications in various fields of mathematics. It's crucial in simplifying fractions, solving problems involving periodic events (like determining when two events will occur simultaneously), and understanding modular arithmetic.
Mathematically, the LCM of two integers a and b, denoted as LCM(a, b), is the smallest positive integer m such that m is a multiple of both a and b. This means that m can be expressed as m = ka and m = lb where k and l are integers.
The relationship between LCM and GCD is formally expressed as:
LCM(a, b) * GCD(a, b) = |a * b|
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
- A: The LCM is the smallest common multiple of two or more numbers, while the GCD is the largest common divisor. They are inversely related, as shown in the formula LCM(a, b) * GCD(a, b) = |a x b|.
-
Q: Why is the LCM important?
- A: The LCM is crucial for simplifying fractions, solving problems involving periodic events, and in various other mathematical contexts like modular arithmetic and abstract algebra.
-
Q: Can the LCM of two numbers be greater than their product?
- A: No, the LCM of two numbers can never be greater than their product. This is evident from the formula: LCM(a,b) = (|a x b|) / GCD(a, b). Since GCD(a,b) is always less than or equal to the smaller of a and b, the LCM will always be less than or equal to the product |a x b|.
-
Q: How do I find the LCM of more than two numbers?
- A: You can extend the prime factorization method or use the iterative approach. For the prime factorization method, find the prime factorization of each number, then take the highest power of each prime factor present in any of the factorizations. The iterative approach involves finding the LCM of two numbers, then finding the LCM of that result and the next number, and so on.
-
Q: What if one of the numbers is 0?
- A: The LCM of any number and 0 is undefined because there is no smallest positive integer that is a multiple of both numbers.
Conclusion:
Finding the LCM of 3 and 8, while seemingly simple, provides a valuable opportunity to explore different mathematical approaches and solidify your understanding of fundamental concepts. Whether you use the method of listing multiples, prime factorization, the GCD relationship, or even Venn diagrams, the answer remains consistent: the LCM of 3 and 8 is 24. Understanding these methods and their underlying principles empowers you to tackle more complex LCM problems and appreciate the broader applications of this critical mathematical concept in various fields. The key takeaway is not just the answer itself, but the mastery of the different techniques and the understanding of the theoretical framework behind them. This will equip you to confidently handle more challenging mathematical problems in the future.
Latest Posts
Latest Posts
-
Sprouting Seeds In A Jar
Sep 16, 2025
-
2000 Meters How Many Miles
Sep 16, 2025
-
Time And Motion Study Sample
Sep 16, 2025
-
Words Start With A A
Sep 16, 2025
-
Beg Crossword Clue 7 Letters
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.