Lcm Of 5 And 4
elan
Sep 12, 2025 · 6 min read
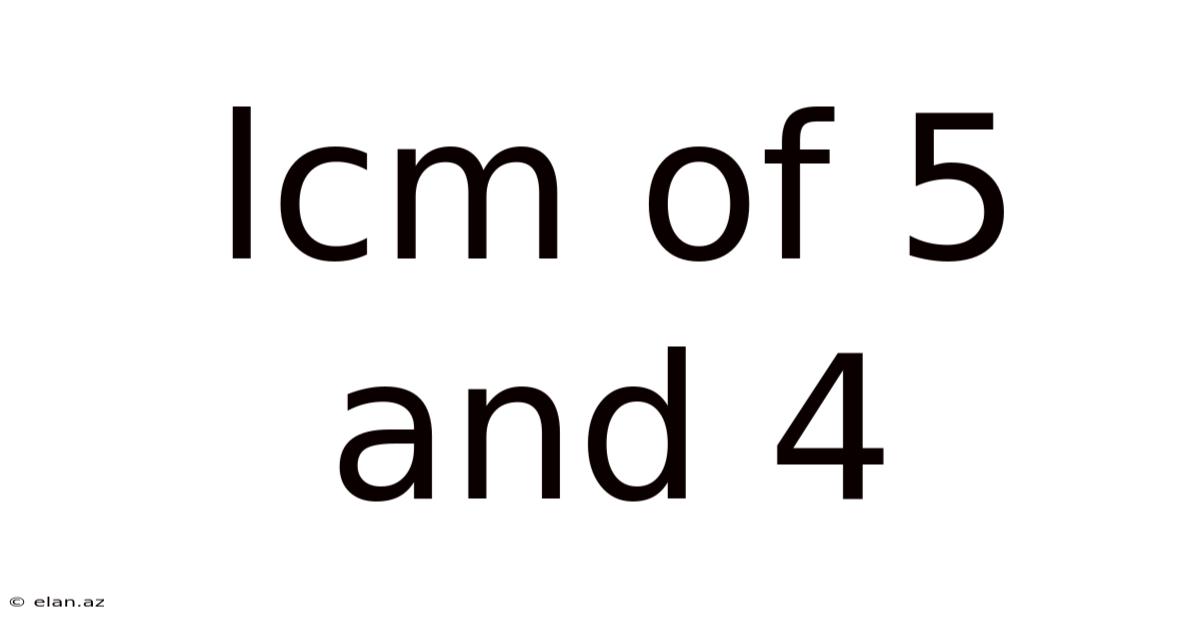
Table of Contents
Understanding the Least Common Multiple (LCM) of 5 and 4: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts opens doors to more complex mathematical applications. This article provides a comprehensive guide to calculating the LCM of 5 and 4, exploring various methods, and delving into the theoretical underpinnings. We'll move beyond a simple answer and explore why this concept is crucial in various mathematical fields and everyday applications.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers you're considering as factors. Understanding LCM is essential in various areas, from simplifying fractions and solving equations to scheduling events and understanding rhythmic patterns in music. This article will focus specifically on finding the LCM of 5 and 4, using different approaches to solidify the concept.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of small numbers like 5 and 4 is by listing their multiples until we find the smallest common one.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45…
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40…
By comparing the lists, we see that the smallest number appearing in both sequences is 20. Therefore, the LCM of 5 and 4 is 20. This method is effective for small numbers, but becomes cumbersome for larger numbers.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves breaking down each number into its prime factors. Prime factorization is the process of expressing a number as a product of its prime numbers (numbers only divisible by 1 and themselves).
- Prime factorization of 5: 5 (5 is a prime number itself)
- Prime factorization of 4: 2 x 2 = 2²
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 2 and 5.
- The highest power of 2 is 2² = 4.
- The highest power of 5 is 5¹ = 5.
Multiplying these highest powers together: 2² x 5 = 4 x 5 = 20. Therefore, the LCM of 5 and 4 is 20. This method is more systematic and scalable to larger numbers.
Method 3: Using the Formula (for two numbers)
For two numbers, a and b, there's a formula that directly relates the LCM and the Greatest Common Divisor (GCD):
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b, and GCD represents the greatest common divisor.
First, we need to find the GCD of 5 and 4. The GCD is the largest number that divides both 5 and 4 without leaving a remainder. In this case, the GCD(5, 4) = 1 (as 1 is the only common divisor).
Now, applying the formula:
LCM(5, 4) = (|5 x 4|) / GCD(5, 4) = 20 / 1 = 20
This formula provides a direct calculation, especially useful when dealing with larger numbers where listing multiples becomes impractical. Finding the GCD itself can be done using various methods like the Euclidean algorithm (explained later).
Method 4: The Euclidean Algorithm for GCD (and consequently LCM)
The Euclidean algorithm is an efficient method for finding the greatest common divisor (GCD) of two numbers. Once we have the GCD, we can use the formula mentioned above to calculate the LCM. Let's illustrate it:
- Divide the larger number by the smaller number and find the remainder: 5 ÷ 4 = 1 with a remainder of 1.
- Replace the larger number with the smaller number, and the smaller number with the remainder: Now we have 4 and 1.
- Repeat the process: 4 ÷ 1 = 4 with a remainder of 0.
- The GCD is the last non-zero remainder: The last non-zero remainder was 1. Therefore, GCD(5, 4) = 1.
Now, using the LCM formula: LCM(5, 4) = (5 x 4) / 1 = 20. The Euclidean algorithm is particularly useful for finding the GCD (and thus the LCM) of much larger numbers.
The Significance of LCM in Various Fields
The concept of LCM extends far beyond simple arithmetic exercises. Its applications are widespread:
-
Fraction Addition and Subtraction: To add or subtract fractions with different denominators, we need to find the LCM of the denominators to obtain a common denominator. This simplifies the calculation significantly.
-
Scheduling and Time Management: Imagine planning events that repeat at different intervals. Finding the LCM helps determine when these events will coincide. For example, if one event happens every 4 days and another every 5 days, the LCM (20) tells us when they'll both occur again on the same day.
-
Music Theory: In music, LCM is crucial in understanding rhythmic patterns. It helps in determining when different rhythmic patterns will synchronize.
-
Gear Ratios in Mechanics: In machinery with multiple gears, the LCM is used to calculate the speed and efficiency of the system.
-
Computer Science: In various algorithms and data structures, the concept of LCM plays a significant role in optimizing performance and resource allocation.
Frequently Asked Questions (FAQ)
-
What if the numbers are very large? For very large numbers, the prime factorization method or the Euclidean algorithm become much more efficient than listing multiples. Software and calculators can handle these calculations easily.
-
Can the LCM of two numbers be one of the numbers themselves? Yes, if one number is a multiple of the other. For example, LCM(4, 8) = 8.
-
What if the numbers share no common factors other than 1? In this case, the GCD is 1, and the LCM is simply the product of the two numbers. This is the case with 5 and 4.
-
Is there a method to find the LCM of more than two numbers? Yes, you can extend the prime factorization method or use iterative applications of the GCD and LCM formulas for two numbers.
Conclusion: Beyond the Simple Calculation
While finding the LCM of 5 and 4 might seem trivial, the process reveals a fundamental concept in mathematics with far-reaching applications. Understanding the different methods—listing multiples, prime factorization, using the formula, and employing the Euclidean algorithm— equips you with tools to tackle more complex problems involving LCM. The ability to find the LCM is not just about solving arithmetic problems; it's about developing a deeper understanding of number theory and its practical implications across various fields. Remember that the key is to choose the most efficient method based on the numbers involved, and appreciate the underlying mathematical principles at play. This understanding will be invaluable as you progress in your mathematical journey.
Latest Posts
Latest Posts
-
What Is 5 Of 10
Sep 12, 2025
-
Diagram Of Changes Of State
Sep 12, 2025
-
What Is The Element Ta
Sep 12, 2025
-
Area And Perimeter Of Rectangle
Sep 12, 2025
-
10 Algebra Questions And Answers
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.