Lcm Of 5 And 9
elan
Sep 14, 2025 · 8 min read
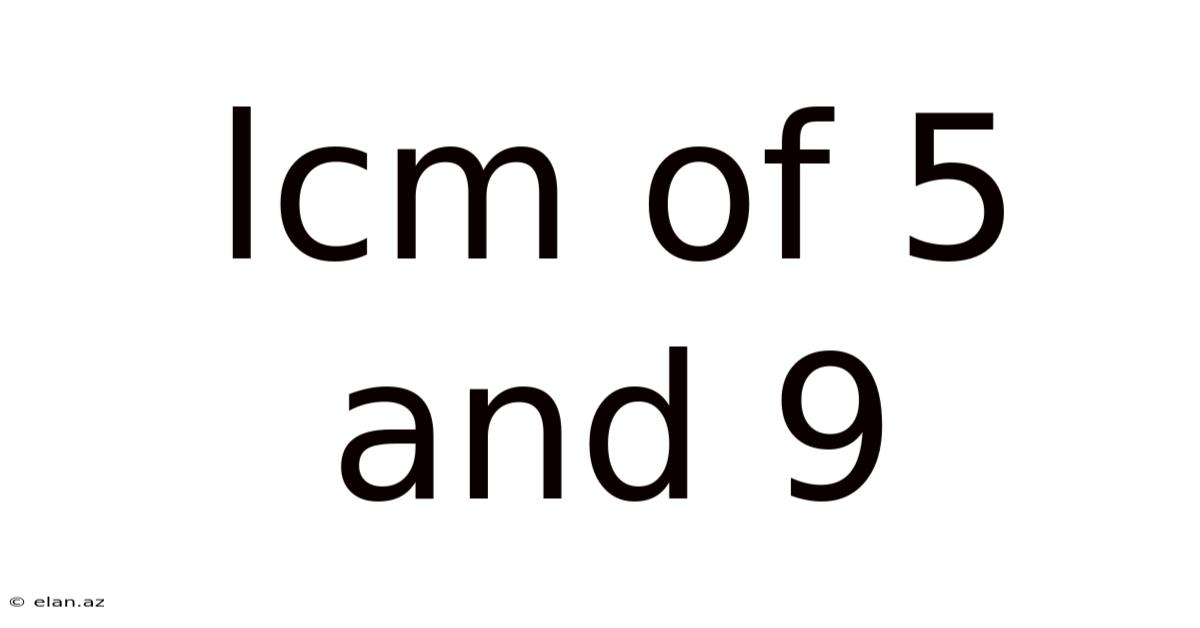
Table of Contents
Understanding the Least Common Multiple (LCM) of 5 and 9: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simple fraction addition to complex algebraic manipulations. This comprehensive guide delves into the LCM of 5 and 9, exploring different methods to calculate it, and providing a deeper understanding of the underlying mathematical principles. We'll break down the process step-by-step, making it accessible to learners of all levels, from elementary school students to those brushing up on their math skills. Understanding the LCM is key to mastering fractions, simplifying expressions, and solving various mathematical problems.
What is the Least Common Multiple (LCM)?
Before we dive into finding the LCM of 5 and 9, let's clarify what the LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the numbers you're considering can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
The concept of LCM has wide-ranging applications. It's essential when:
- Adding or subtracting fractions: Finding a common denominator for fractions requires determining the LCM of the denominators.
- Solving problems involving cycles or periodic events: Determining when events will coincide (e.g., two buses arriving at the same stop simultaneously) relies on finding the LCM of their respective cycles.
- Simplifying algebraic expressions: LCM is used to simplify fractions containing variables.
- Number theory: The LCM plays a crucial role in various number theory problems, including those involving modular arithmetic and divisibility.
Method 1: Listing Multiples
The simplest method to find the LCM of 5 and 9 is by listing their multiples until a common multiple is found. Let's start by listing the multiples of each number:
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, ...
Multiples of 9: 9, 18, 27, 36, 45, 54, 63, ...
By comparing the two lists, we can see that the smallest number that appears in both lists is 45. Therefore, the LCM of 5 and 9 is 45. This method is straightforward for smaller numbers, but becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, is to use prime factorization. This method involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
-
Prime Factorization of 5: 5 is a prime number itself, so its prime factorization is simply 5.
-
Prime Factorization of 9: 9 = 3 x 3 = 3².
-
Finding the LCM: To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations of both numbers. In this case, we have the prime factors 3 and 5. The highest power of 3 is 3² (from the factorization of 9), and the highest power of 5 is 5 (from the factorization of 5). Therefore, the LCM is 3² x 5 = 9 x 5 = 45.
This method is significantly more efficient for larger numbers because it avoids the tedious process of listing multiples. It's a fundamental technique used in many areas of mathematics.
Method 3: Using the Formula (for two numbers)
For two numbers, a and b, there's a handy formula relating the LCM and the Greatest Common Divisor (GCD):
LCM(a, b) = (|a x b|) / GCD(a, b)
Where |a x b| represents the absolute value of the product of a and b, and GCD(a, b) is the greatest common divisor of a and b.
Let's apply this to find the LCM of 5 and 9:
-
Find the GCD of 5 and 9: The GCD is the largest number that divides both 5 and 9 without leaving a remainder. Since 5 and 9 share no common factors other than 1, their GCD is 1.
-
Apply the formula: LCM(5, 9) = (|5 x 9|) / GCD(5, 9) = 45 / 1 = 45
This formula provides a direct calculation, but it requires first calculating the GCD. The GCD can be found using various methods, including prime factorization or the Euclidean algorithm (explained later).
Method 4: The Euclidean Algorithm (for finding GCD, then using the formula)
The Euclidean algorithm is an efficient method for finding the greatest common divisor (GCD) of two numbers. Once we have the GCD, we can use the formula from Method 3 to calculate the LCM.
The Euclidean algorithm works by repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD. Let's find the GCD of 5 and 9:
-
Divide the larger number (9) by the smaller number (5): 9 = 1 x 5 + 4
-
Replace the larger number with the smaller number (5) and the smaller number with the remainder (4): 5 = 1 x 4 + 1
-
Repeat the process: 4 = 4 x 1 + 0
The last non-zero remainder is 1, so the GCD(5, 9) = 1. Now, using the formula from Method 3: LCM(5, 9) = (5 x 9) / 1 = 45.
The Euclidean algorithm is particularly useful for finding the GCD of larger numbers where prime factorization might be more time-consuming.
Why is Understanding LCM Important?
Understanding the least common multiple extends beyond simple arithmetic calculations. It underpins several critical concepts and applications in mathematics and other fields. Here are some key reasons why mastering LCM is crucial:
-
Fraction Operations: Adding, subtracting, and comparing fractions necessitate finding a common denominator, which is essentially the LCM of the denominators. Without understanding LCM, accurate fraction calculations become impossible.
-
Scheduling and Pattern Recognition: LCM finds applications in scheduling problems. For example, determining when two cyclical events will occur simultaneously requires calculating the LCM of their cycles. This applies to various real-world scenarios, such as predicting the simultaneous arrival of buses or the alignment of planets.
-
Modular Arithmetic: In number theory, LCM plays a vital role in modular arithmetic, where operations are performed on remainders after division by a specific number (the modulus). Understanding LCM is key to solving congruence problems and other number theory applications.
-
Algebraic Simplification: LCM is critical for simplifying algebraic expressions involving fractions with variables. Finding the LCM of the denominators allows us to combine fractions and simplify complex expressions.
-
Rhythm and Music: In music theory, LCM helps determine the least common denominator for different rhythmic patterns, allowing musicians to create harmonious and synchronized compositions.
Frequently Asked Questions (FAQ)
Q: What if I want to find the LCM of more than two numbers?
A: For more than two numbers, you can extend the prime factorization method. Find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations. Multiply these highest powers together to get the LCM. The formula-based methods don't directly extend to more than two numbers easily.
Q: Is there a fastest way to find the LCM?
A: The fastest method depends on the numbers involved. For small numbers, listing multiples is quick. For larger numbers, prime factorization is generally the most efficient, especially when combined with the formula involving the GCD and using the Euclidean algorithm for finding the GCD.
Q: What if one of the numbers is zero?
A: The LCM of any number and zero is undefined. This is because zero is a divisor of all numbers, meaning there is no smallest positive number that is divisible by both the other number and zero.
Q: Can the LCM be smaller than one of the numbers?
A: No, the LCM will always be greater than or equal to the largest of the numbers involved.
Q: What is the relationship between LCM and GCD?
A: The LCM and GCD of two numbers are inversely related. As the GCD increases, the LCM decreases, and vice versa. For example, if the GCD is large, the LCM will be relatively small, and the two numbers are closely related. The formula LCM(a, b) = (|a x b|) / GCD(a, b) directly demonstrates this relationship.
Conclusion
Finding the least common multiple of 5 and 9, which is 45, is a simple yet illustrative example of a fundamental mathematical concept. We've explored several methods for calculating the LCM, each offering a different approach and highlighting the importance of understanding prime factorization and the relationship between LCM and GCD. Mastering the LCM is not just about solving specific problems; it's about developing a deeper understanding of number theory and its applications in various fields. The skills learned in calculating LCM are essential for success in higher-level mathematics and problem-solving in numerous real-world contexts. Remember, understanding the underlying principles is as important as the ability to apply the methods efficiently.
Latest Posts
Latest Posts
-
Metres To Square Metres Converter
Sep 14, 2025
-
Words That End In Or
Sep 14, 2025
-
Hcf Of 210 And 350
Sep 14, 2025
-
Formation Of Geese In Flight
Sep 14, 2025
-
What Is 220cm In Feet
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.