Lcm Of 60 And 220
elan
Sep 10, 2025 · 6 min read
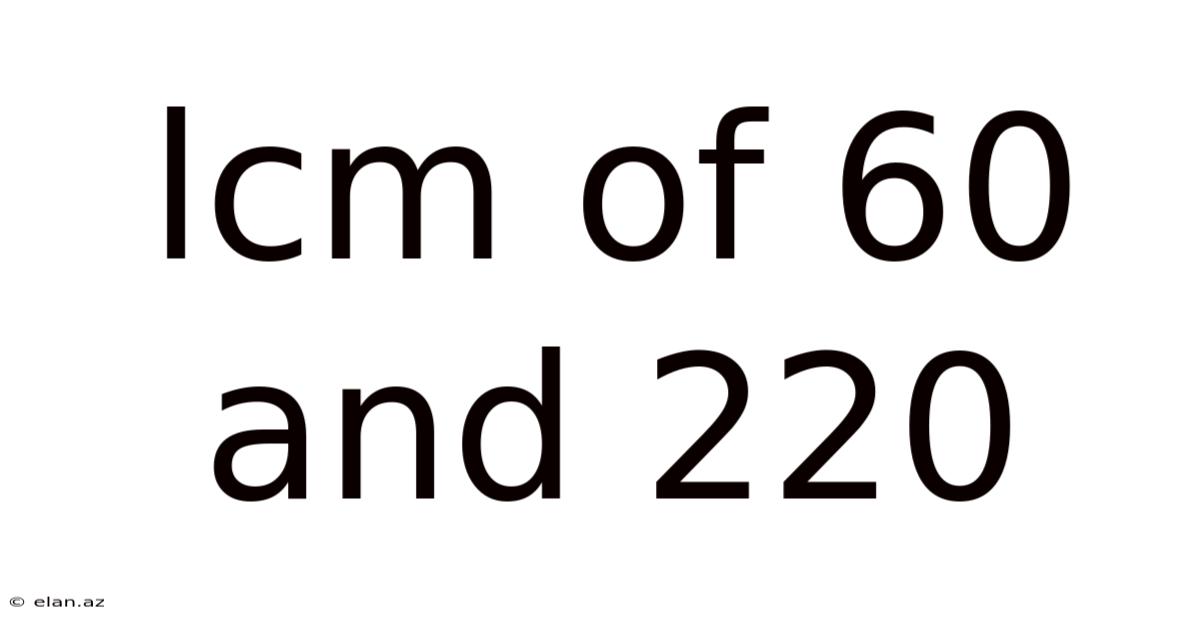
Table of Contents
Finding the LCM of 60 and 220: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, with applications ranging from simple fraction addition to complex scheduling problems. This article will delve deep into calculating the LCM of 60 and 220, exploring various methods and providing a thorough understanding of the underlying principles. We'll move beyond a simple answer, offering insights into prime factorization, the Euclidean algorithm, and practical applications to solidify your understanding of this important mathematical concept.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. Understanding LCM is crucial for solving problems involving fractions, finding common denominators, and synchronizing cyclical events. For instance, if you have two gears rotating at different speeds, the LCM helps determine when they'll both be at their starting position simultaneously.
Method 1: Prime Factorization
This is arguably the most common and conceptually straightforward method for finding the LCM. It involves breaking down each number into its prime factors – the smallest prime numbers that multiply together to give the original number.
Step 1: Prime Factorization of 60
60 can be factored as follows:
60 = 2 x 30 = 2 x 2 x 15 = 2 x 2 x 3 x 5 = 2² x 3 x 5
Therefore, the prime factorization of 60 is 2² x 3 x 5.
Step 2: Prime Factorization of 220
Now, let's find the prime factorization of 220:
220 = 2 x 110 = 2 x 2 x 55 = 2 x 2 x 5 x 11 = 2² x 5 x 11
Thus, the prime factorization of 220 is 2² x 5 x 11.
Step 3: Identifying Common and Unique Prime Factors
Compare the prime factorizations of 60 and 220. We identify the common and unique prime factors:
- Common: 2² and 5
- Unique to 60: 3
- Unique to 220: 11
Step 4: Calculating the LCM
To calculate the LCM, we multiply the highest power of each prime factor present in either factorization:
LCM(60, 220) = 2² x 3 x 5 x 11 = 4 x 3 x 5 x 11 = 660
Therefore, the least common multiple of 60 and 220 is 660.
Method 2: Using the Greatest Common Divisor (GCD)
Another effective method involves using the greatest common divisor (GCD), also known as the highest common factor (HCF). The relationship between LCM and GCD is defined by the following formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
Step 1: Finding the GCD of 60 and 220
We can use the Euclidean algorithm to find the GCD. The Euclidean algorithm is an efficient method for finding the greatest common divisor of two integers.
- Divide the larger number (220) by the smaller number (60): 220 ÷ 60 = 3 with a remainder of 40.
- Replace the larger number with the smaller number (60) and the smaller number with the remainder (40): 60 ÷ 40 = 1 with a remainder of 20.
- Repeat the process: 40 ÷ 20 = 2 with a remainder of 0.
- The last non-zero remainder is the GCD. In this case, the GCD(60, 220) = 20.
Step 2: Calculating the LCM using the GCD
Now, we can use the formula relating LCM and GCD:
LCM(60, 220) = (60 x 220) / GCD(60, 220) = (60 x 220) / 20 = 660
This confirms that the LCM of 60 and 220 is 660.
Method 3: Listing Multiples
This method is more suitable for smaller numbers. It involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
Multiples of 60: 60, 120, 180, 240, 300, 360, 420, 480, 540, 600, 660, ...
Multiples of 220: 220, 440, 660, ...
The smallest common multiple is 660. While effective for smaller numbers, this method becomes less practical for larger numbers.
Explanation of the Mathematical Principles
The methods above rely on fundamental number theory concepts. Prime factorization demonstrates that every integer greater than 1 can be uniquely represented as a product of prime numbers. This uniqueness allows us to systematically find the LCM by considering the highest powers of each prime factor present in the numbers.
The Euclidean algorithm, used in the GCD method, is based on the principle that the GCD of two numbers remains unchanged if the larger number is replaced by its difference with the smaller number. This iterative process efficiently reduces the numbers until the GCD is found. The formula linking LCM and GCD is a direct consequence of the prime factorization theorem.
Real-World Applications of LCM
The concept of LCM has numerous practical applications:
- Scheduling: Determining when events will occur simultaneously. For example, finding when two buses with different schedules will arrive at the same stop together.
- Fraction Addition and Subtraction: Finding the least common denominator to simplify operations with fractions.
- Gear Ratios: Calculating the synchronization of rotating gears with different speeds.
- Music Theory: Determining the least common multiple of note durations to understand rhythmic patterns.
- Project Management: Scheduling tasks that depend on the completion of others.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The least common multiple (LCM) is the smallest number that is a multiple of both numbers, while the greatest common divisor (GCD) is the largest number that divides both numbers without leaving a remainder.
Q: Can the LCM of two numbers be smaller than the larger number?
A: No. The LCM is always greater than or equal to the larger of the two numbers.
Q: Is there a formula for finding the LCM of more than two numbers?
A: Yes. You can extend the prime factorization method or the GCD-based method to find the LCM of multiple numbers. You would find the prime factorization of each number, then take the highest power of each prime factor present across all numbers and multiply them together.
Q: What if the two numbers are coprime (their GCD is 1)?
A: If two numbers are coprime, their LCM is simply the product of the two numbers. For example, LCM(7, 15) = 7 x 15 = 105 because the GCD(7, 15) = 1.
Conclusion
Finding the LCM of 60 and 220, as demonstrated through various methods, highlights the importance of understanding fundamental mathematical concepts. The prime factorization method offers a clear, intuitive approach, while the GCD method leverages an efficient algorithm. The ability to calculate LCM efficiently has wide-ranging applications across various fields, making it an essential skill for anyone working with numbers. This comprehensive guide aims to not only provide the solution (660) but also to deepen your understanding of LCM and its relevance in practical contexts. Remember, mastering these concepts empowers you to tackle more complex mathematical problems confidently.
Latest Posts
Latest Posts
-
Difference Between Affection And Effection
Sep 10, 2025
-
3500 Sq Ft In Meters
Sep 10, 2025
-
149cm In Feet And Inches
Sep 10, 2025
-
Raksha Bandhan Message For Brother
Sep 10, 2025
-
Words Ending With A D
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 60 And 220 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.