Lcm Of 70 And 273
elan
Sep 11, 2025 · 6 min read
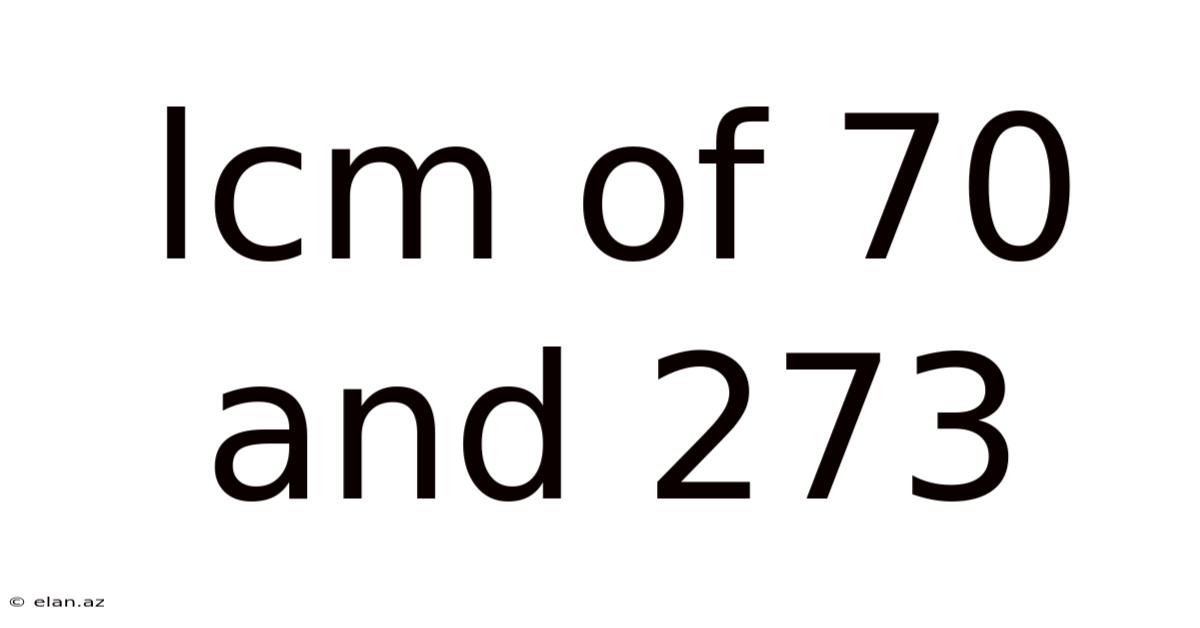
Table of Contents
Finding the Least Common Multiple (LCM) of 70 and 273: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and exploring different methods can significantly enhance your mathematical skills. This article will delve deep into calculating the LCM of 70 and 273, explaining multiple approaches and providing a solid foundation for tackling similar problems. We'll explore the concept of LCM, its applications, and various methods for calculating it, focusing on efficiency and clarity. This will equip you with the knowledge to not only solve this specific problem but also confidently handle a wide range of LCM calculations.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers. It's a fundamental concept in number theory with practical applications in various fields, including scheduling, fractions, and even music theory. Understanding LCM is crucial for simplifying fractions, solving problems involving cycles or repetitions, and determining the smallest common denominator. Let's explore how to find the LCM of 70 and 273.
Method 1: Prime Factorization
This method is considered one of the most efficient and fundamental ways to determine the LCM of two or more numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Step 1: Find the prime factorization of 70.
70 can be factored as follows:
70 = 2 x 35 = 2 x 5 x 7
Therefore, the prime factorization of 70 is 2¹ x 5¹ x 7¹.
Step 2: Find the prime factorization of 273.
273 can be factored as follows:
273 = 3 x 91 = 3 x 7 x 13
Therefore, the prime factorization of 273 is 3¹ x 7¹ x 13¹.
Step 3: Identify the highest power of each prime factor.
Comparing the prime factorizations of 70 and 273, we have the following prime factors: 2, 3, 5, 7, and 13. We take the highest power of each prime factor present in either factorization:
- 2¹
- 3¹
- 5¹
- 7¹
- 13¹
Step 4: Multiply the highest powers together.
To find the LCM, we multiply the highest powers of all the prime factors together:
LCM(70, 273) = 2¹ x 3¹ x 5¹ x 7¹ x 13¹ = 2 x 3 x 5 x 7 x 13 = 2730
Therefore, the least common multiple of 70 and 273 is 2730.
Method 2: Listing Multiples
This method is simpler for smaller numbers but becomes less efficient as the numbers get larger. It involves listing the multiples of each number until a common multiple is found.
Step 1: List multiples of 70.
Multiples of 70: 70, 140, 210, 280, 350, 420, 490, 560, 630, 700, 770, 840, 910, 980, 1050, 1120, 1190, 1260, 1330, 1400, 1470, 1540, 1610, 1680, 1750, 1820, 1890, 1960, 2030, 2100, 2170, 2240, 2310, 2380, 2450, 2520, 2590, 2660, 2730...
Step 2: List multiples of 273.
Multiples of 273: 273, 546, 819, 1092, 1365, 1638, 1911, 2184, 2457, 2730...
Step 3: Identify the smallest common multiple.
By comparing the lists, we can see that the smallest common multiple of 70 and 273 is 2730. This method is less efficient for larger numbers because it requires generating a large number of multiples before finding the common one.
Method 3: Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest positive integer that divides both numbers without leaving a remainder.
Step 1: Find the GCD of 70 and 273 using the Euclidean algorithm.
The Euclidean algorithm is an efficient method for finding the GCD.
- Divide 273 by 70: 273 = 3 x 70 + 63
- Divide 70 by 63: 70 = 1 x 63 + 7
- Divide 63 by 7: 63 = 9 x 7 + 0
The last non-zero remainder is 7, so the GCD(70, 273) = 7.
Step 2: Apply the LCM formula.
LCM(70, 273) = (70 x 273) / GCD(70, 273) = (70 x 273) / 7 = 10 x 273 = 2730
Therefore, the least common multiple of 70 and 273 is 2730. This method is quite efficient, especially for larger numbers, as finding the GCD is generally faster than listing multiples.
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method offers a powerful and insightful approach to understanding LCM. It reveals the fundamental building blocks of the numbers involved and highlights the relationship between the numbers and their multiples. Each prime factor represents an indivisible unit, and the highest power of each prime factor ensures that the resulting LCM is divisible by both original numbers. This method's elegance lies in its ability to directly address the core components of the numbers, rather than relying on iterative processes. It’s a foundational concept that extends far beyond basic LCM calculations, finding application in more advanced mathematical concepts.
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond the classroom. It finds practical applications in diverse fields:
-
Scheduling: Imagine two buses that depart from a terminal at different intervals. The LCM of their intervals determines when they will depart at the same time again.
-
Fractions: Finding the LCM of the denominators is crucial for adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculation.
-
Music Theory: The LCM is used to determine the least common period of musical rhythms. Understanding the LCM ensures that musical phrases align and harmonize correctly.
-
Project Management: In project scheduling, LCM can be helpful in determining when different tasks or stages will coincide, helping in optimizing resource allocation and project timelines.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The least common multiple (LCM) is the smallest positive integer that is a multiple of all the given integers. The greatest common divisor (GCD) is the largest positive integer that divides all the given integers without leaving a remainder. They are inversely related; as the GCD increases, the LCM decreases, and vice versa.
Q: Can the LCM of two numbers be equal to one of the numbers?
A: Yes, if one number is a multiple of the other. For example, LCM(6, 12) = 12.
Q: What if I have more than two numbers? How do I find the LCM?
A: You can extend the prime factorization method. Find the prime factorization of each number, identify the highest power of each prime factor present in any of the factorizations, and multiply those highest powers together. The formula-based method can also be extended using the concept of pairwise LCM calculations.
Q: Why is the prime factorization method preferred for larger numbers?
A: The prime factorization method is more efficient for larger numbers because it directly addresses the fundamental building blocks of the numbers, avoiding the iterative processes involved in listing multiples. It provides a more structured and concise approach to finding the LCM.
Conclusion
Calculating the least common multiple of 70 and 273, as demonstrated, underscores the importance of understanding fundamental mathematical concepts. We explored three distinct methods – prime factorization, listing multiples, and using the LCM formula – each with its strengths and weaknesses. The prime factorization method emerges as the most robust and efficient, particularly when dealing with larger numbers. Beyond the immediate calculation, this exercise highlights the broader applicability of LCM across various fields. Mastering this concept opens doors to a more comprehensive understanding of number theory and its practical implications in diverse real-world scenarios. Remember, the key to mathematical proficiency lies not just in the ability to find the answer but also in understanding the underlying principles and choosing the most appropriate method for the task at hand.
Latest Posts
Latest Posts
-
3 Foot 6 In Cm
Sep 11, 2025
-
Verbs That Start With R
Sep 11, 2025
-
Branch Of Maths 8 Letters
Sep 11, 2025
-
How Can We Decrease Friction
Sep 11, 2025
-
Is 151 A Prime Number
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 70 And 273 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.