Lcm Of 90 And 72
elan
Sep 10, 2025 · 5 min read
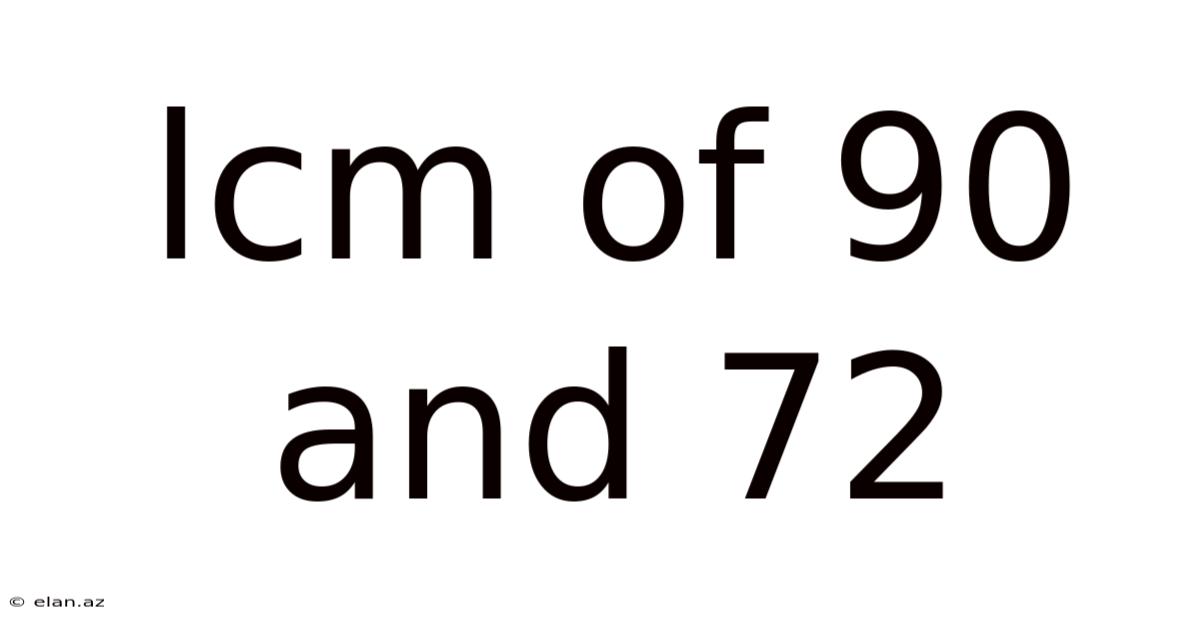
Table of Contents
Finding the LCM of 90 and 72: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with applications ranging from simple fraction addition to complex scheduling problems. This article provides a comprehensive guide to calculating the LCM of 90 and 72, exploring various methods, explaining the underlying mathematical principles, and answering frequently asked questions. We'll delve into both the manual calculation methods and explore how to use these concepts in more complex scenarios. Understanding LCM is crucial for anyone working with fractions, ratios, and cyclical events.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 90 and 72, let's establish a clear understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both numbers divide into evenly. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Method 1: Listing Multiples
The most straightforward method to find the LCM of 90 and 72 is by listing their multiples until you find the smallest common one.
- Multiples of 90: 90, 180, 270, 360, 450, 540, 630, 720, 810, 900, ...
- Multiples of 72: 72, 144, 216, 288, 360, 432, 504, 576, 648, 720, ...
By comparing the lists, we can see that the smallest common multiple is 360. Therefore, the LCM of 90 and 72 is 360. While this method works well for smaller numbers, it becomes increasingly impractical as the numbers get larger.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves using prime factorization. This method breaks down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Prime Factorize 90
90 = 2 × 45 = 2 × 3 × 15 = 2 × 3 × 3 × 5 = 2¹ × 3² × 5¹
Step 2: Prime Factorize 72
72 = 2 × 36 = 2 × 2 × 18 = 2 × 2 × 2 × 9 = 2 × 2 × 2 × 3 × 3 = 2³ × 3²
Step 3: Identify the Highest Power of Each Prime Factor
Now, we identify the highest power of each prime factor present in either factorization:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3² = 9
- Highest power of 5: 5¹ = 5
Step 4: Multiply the Highest Powers Together
Finally, multiply the highest powers together to find the LCM:
LCM(90, 72) = 2³ × 3² × 5¹ = 8 × 9 × 5 = 360
Therefore, the LCM of 90 and 72, using prime factorization, is 360. This method is significantly more efficient than listing multiples, particularly when dealing with larger numbers.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the Greatest Common Divisor (GCD) of two numbers are closely related. We can use the GCD to calculate the LCM using the following formula:
LCM(a, b) = (|a × b|) / GCD(a, b)
where '|a × b|' represents the absolute value of the product of a and b.
Step 1: Find the GCD of 90 and 72 using the Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCD.
- Divide the larger number (90) by the smaller number (72): 90 = 1 × 72 + 18
- Replace the larger number with the smaller number (72) and the smaller number with the remainder (18): 72 = 4 × 18 + 0
Since the remainder is 0, the GCD is the last non-zero remainder, which is 18.
Step 2: Apply the Formula
Now, we apply the formula:
LCM(90, 72) = (90 × 72) / GCD(90, 72) = (90 × 72) / 18 = 360
Again, the LCM of 90 and 72 is 360. This method highlights the interconnectedness between LCM and GCD, offering another efficient approach to solving the problem.
Real-World Applications of LCM
The concept of LCM extends far beyond textbook exercises. Here are some real-world applications:
-
Scheduling: Imagine two buses depart from the same station. One bus departs every 90 minutes, and the other departs every 72 minutes. The LCM (360 minutes, or 6 hours) represents the time when both buses will depart simultaneously again.
-
Fractions: When adding or subtracting fractions, finding the LCM of the denominators is crucial for obtaining a common denominator.
-
Patterning: In various cyclical patterns, whether in music, art, or nature, understanding LCM helps predict when patterns will repeat.
-
Construction and Engineering: LCM plays a vital role in determining the optimal lengths or sizes of materials in construction and engineering projects.
Frequently Asked Questions (FAQ)
-
Q: Is there only one LCM for two numbers? A: Yes, there is only one least common multiple for any pair of numbers.
-
Q: What if one of the numbers is 0? A: The LCM of any number and 0 is undefined.
-
Q: Can the LCM of two numbers be smaller than one of the numbers? A: No, the LCM is always greater than or equal to the larger of the two numbers.
-
Q: How can I check if my calculated LCM is correct? A: Ensure that your calculated LCM is divisible by both original numbers.
Conclusion
Calculating the least common multiple (LCM) is a fundamental skill with widespread applications. We have explored three effective methods: listing multiples, prime factorization, and the GCD method. The prime factorization method proves particularly useful for larger numbers due to its efficiency. Understanding LCM is not just about solving mathematical problems; it's about grasping a crucial concept with practical implications across numerous fields. Remember, practice is key to mastering these techniques. Try calculating the LCM of different number pairs to build your understanding and confidence. By understanding the underlying principles and choosing the appropriate method, you can confidently tackle any LCM problem that comes your way.
Latest Posts
Latest Posts
-
Where Do I Buy Borax
Sep 10, 2025
-
Descriptive Words Starting With V
Sep 10, 2025
-
Square Yards To Square Meters
Sep 10, 2025
-
Words That Rhyme With Rhyme
Sep 10, 2025
-
Nouns That Start With H
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 90 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.