One Half In Decimal Form
elan
Sep 19, 2025 · 5 min read
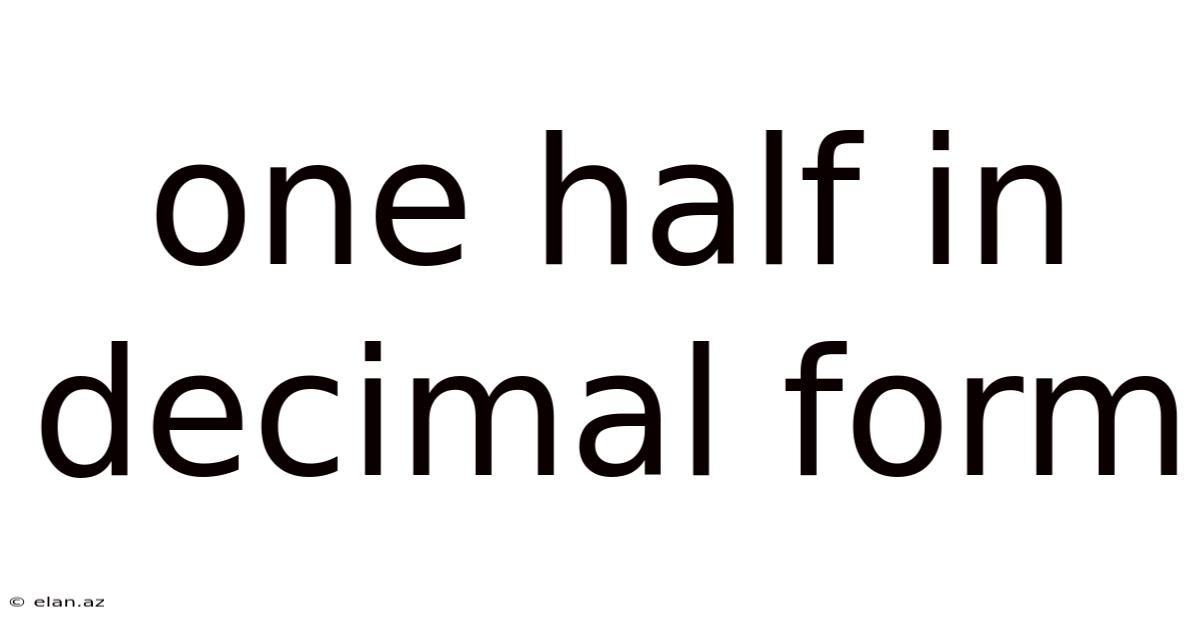
Table of Contents
One Half in Decimal Form: A Comprehensive Exploration
Understanding fractions and their decimal equivalents is fundamental to mathematics and its applications in everyday life. This article delves into the concept of one-half (1/2) and its decimal representation, exploring its calculation, significance, and applications across various fields. We'll go beyond the simple answer and uncover the underlying principles, offering a deeper understanding of this seemingly simple concept. This exploration will cover different methods of conversion, address common misconceptions, and highlight the importance of decimal representation in practical scenarios.
Introduction: Understanding Fractions and Decimals
Before diving into the specifics of one-half, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/2, 1 is the numerator and 2 is the denominator. This signifies one part out of two equal parts.
A decimal, on the other hand, represents a number using a base-10 system. It utilizes a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For instance, 0.5 represents five-tenths.
The ability to convert between fractions and decimals is crucial for various mathematical operations and real-world applications. This article focuses on the conversion of one-half (1/2) to its decimal equivalent.
Calculating One-Half in Decimal Form: The Long Division Method
The most straightforward method to convert a fraction to a decimal is through long division. To convert 1/2 to a decimal, we divide the numerator (1) by the denominator (2):
1 ÷ 2 = 0.5
This division yields a quotient of 0.5, meaning one-half is equal to 0.5 in decimal form. The process is simple: 2 goes into 1 zero times, so we add a decimal point and a zero. 2 goes into 10 five times, resulting in a remainder of zero. Therefore, the decimal representation of 1/2 is exactly 0.5.
Alternative Methods: Understanding the Relationship Between Fractions and Decimals
While long division is a reliable method, understanding the underlying relationship between fractions and decimals provides valuable insights. We can also consider the following:
-
Place Value: The fraction 1/2 represents one part out of two equal parts. Since decimals are based on powers of 10, we can think of 1/2 as representing x/10, where x is the number of tenths. Since 1/2 is equivalent to 5/10, we can directly express it as 0.5.
-
Equivalent Fractions: Creating equivalent fractions with a denominator that is a power of 10 simplifies the conversion. We can multiply both the numerator and denominator of 1/2 by 5 to get 5/10, which is directly convertible to the decimal 0.5. This method helps visualize the fractional part as a decimal.
The Significance of 0.5: Applications in Various Fields
The decimal representation of one-half, 0.5, has significant implications across numerous fields:
-
Mathematics: 0.5 is a crucial value in various mathematical operations, including calculations involving percentages, averages, and proportions. It serves as a fundamental benchmark for understanding halves and their relationship to whole numbers.
-
Science: In scientific measurements, 0.5 often represents a midpoint or halfway point in a scale or measurement. For example, in measuring temperature, 0.5 might represent a halfway point between two degree markings.
-
Engineering: Engineering designs often utilize 0.5 in calculations involving dimensions, proportions, and tolerances. Accurate decimal representation is crucial for precise engineering measurements.
-
Finance: Financial calculations frequently use 0.5 to represent half of a unit, such as half a share of stock or half a percentage point in interest rates.
-
Everyday Life: We encounter 0.5 frequently in everyday life, such as when dividing something in half, calculating discounts, or determining half a quantity.
Common Misconceptions and Clarifications
Despite its simplicity, some misconceptions surround the decimal representation of one-half:
-
Confusion with other fractions: It’s important to differentiate 0.5 (one-half) from other decimals, like 0.1 (one-tenth) or 0.25 (one-quarter). Understanding the distinct values of these decimals is vital for accurate calculations.
-
Rounding errors: While 0.5 is an exact decimal, rounding errors can occur when using 0.5 in more complex calculations involving other approximations. Being aware of potential rounding errors is crucial for achieving accuracy in computations.
-
Improper use in specific contexts: In some contexts, using the fraction 1/2 might be preferred over 0.5 for clarity or to avoid ambiguity, especially in written communication or specialized fields.
Frequently Asked Questions (FAQ)
-
Q: Is 0.5 the only decimal representation of one-half?
- A: Yes, 0.5 is the exact decimal representation of one-half. There are no other equivalent decimal representations.
-
Q: Can I express one-half as a percentage?
- A: Yes, one-half is equivalent to 50%.
-
Q: How can I convert other fractions to decimals?
- A: You can use long division or find an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.).
-
Q: What are some real-world examples where understanding 0.5 is important?
- A: Examples include calculating half a recipe, sharing something equally, determining the midpoint of a distance, or calculating discounts.
-
Q: Why is it important to understand the relationship between fractions and decimals?
- A: This understanding is fundamental for performing calculations involving both fractions and decimals, essential across numerous fields, from basic arithmetic to advanced mathematics and science.
Conclusion: Mastering the Fundamentals
Understanding the decimal representation of one-half—0.5—is a foundational element in mathematics and its applications. This exploration has demonstrated various methods for converting fractions to decimals, emphasizing the importance of clear understanding and accurate calculation. Beyond the simple answer, we've delved into the underlying principles, clarifying common misconceptions and highlighting the diverse applications of 0.5 across different fields. Mastering this concept opens doors to a deeper appreciation of mathematical principles and their significance in our daily lives. From simple everyday calculations to complex scientific and engineering applications, the ability to effortlessly convert between fractions and decimals is a vital skill that empowers informed decision-making and problem-solving.
Latest Posts
Latest Posts
-
Flowers That Start With I
Sep 19, 2025
-
25 000 Rupees In Pounds
Sep 19, 2025
-
What Is A Scheduled Caste
Sep 19, 2025
-
What Does An Animal Eat
Sep 19, 2025
-
Sample Letter Of Salary Increment
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about One Half In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.