Prime Factor Decomposition Of 252
elan
Sep 11, 2025 · 6 min read
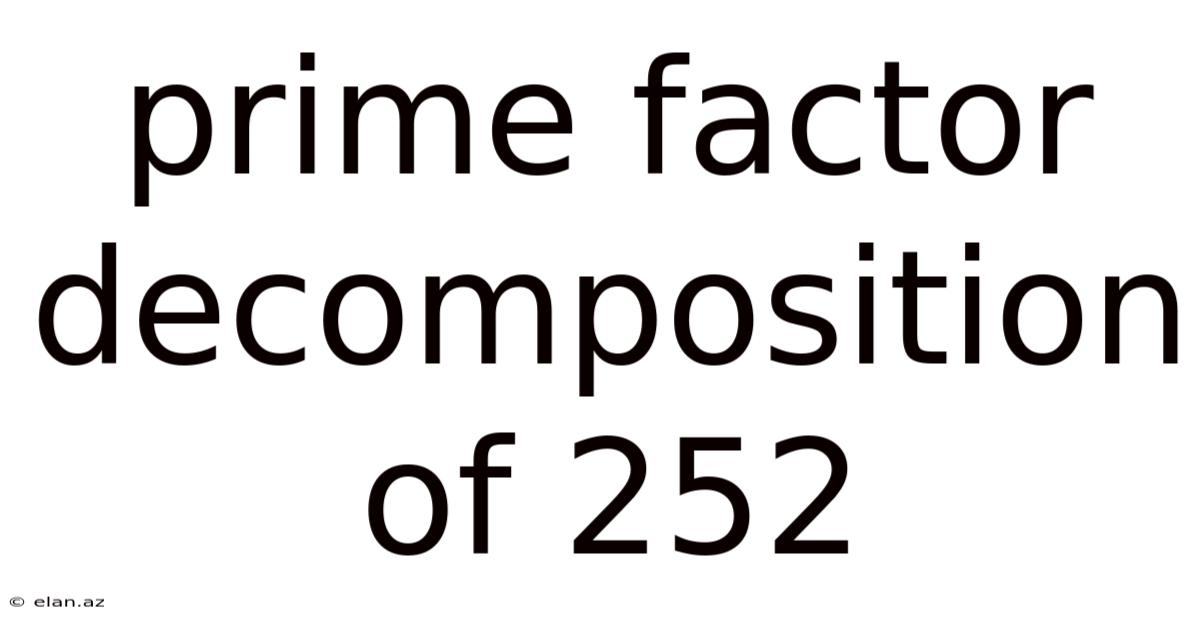
Table of Contents
Prime Factor Decomposition of 252: A Deep Dive into Number Theory
Finding the prime factorization of a number might seem like a simple task, especially for smaller numbers like 252. However, understanding the process thoroughly unveils fundamental concepts in number theory, paving the way for more advanced mathematical explorations. This article will guide you through the prime factor decomposition of 252, explaining the method, the underlying theory, and its broader applications. We'll also delve into related concepts to solidify your understanding.
Understanding Prime Numbers and Factorization
Before diving into the decomposition of 252, let's establish a solid foundation. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Numbers that are not prime are called composite numbers.
Factorization, in its simplest form, is the process of expressing a number as a product of its factors. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. However, prime factorization specifically involves expressing a number as a product of only its prime factors. This representation is unique for every number (except for the order of the factors). This uniqueness is guaranteed by the Fundamental Theorem of Arithmetic.
The Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic is a cornerstone of number theory. It states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This theorem ensures that the prime factorization of a number is a unique and definitive representation. This uniqueness is crucial in many areas of mathematics, particularly in algebra and cryptography.
Finding the Prime Factorization of 252: A Step-by-Step Guide
Now, let's tackle the prime factorization of 252. We'll use a method called the factor tree.
-
Start with the smallest prime number: We begin by dividing 252 by the smallest prime number, 2. 252 ÷ 2 = 126.
-
Continue dividing by prime numbers: Now we have 126. This is also divisible by 2: 126 ÷ 2 = 63.
-
Move to the next prime: 63 is not divisible by 2, but it is divisible by 3: 63 ÷ 3 = 21.
-
Keep going: 21 is also divisible by 3: 21 ÷ 3 = 7.
-
Finish with a prime: We're left with 7, which is a prime number.
Therefore, the prime factorization of 252 is 2 x 2 x 3 x 3 x 7, which can be written more concisely as 2² x 3² x 7.
This can be visually represented using a factor tree:
252
/ \
2 126
/ \
2 63
/ \
3 21
/ \
3 7
Applications of Prime Factorization
The seemingly simple process of prime factorization has surprisingly wide-ranging applications across various fields:
-
Cryptography: Prime numbers are fundamental to modern encryption methods like RSA. The security of these systems relies on the difficulty of factoring very large numbers into their prime components.
-
Number Theory: Prime factorization is crucial for understanding many concepts within number theory, such as modular arithmetic, greatest common divisors (GCD), and least common multiples (LCM).
-
Computer Science: Algorithms for finding prime factors are important in areas like computer security and database management. Efficient algorithms are continuously being developed to tackle the computational challenges of factoring large numbers.
-
Abstract Algebra: Prime factorization has implications in abstract algebra, especially in ring theory and field theory. Understanding prime ideals is essential for studying the structure of rings.
Calculating the Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Prime factorization provides a straightforward method for calculating the GCD and LCM of two or more numbers.
Greatest Common Divisor (GCD): The GCD is the largest number that divides all the given numbers without leaving a remainder. Using prime factorization, we find the common prime factors raised to the lowest power and multiply them together.
Let's find the GCD of 252 and 360. First, we find their prime factorizations:
- 252 = 2² x 3² x 7
- 360 = 2³ x 3² x 5
The common prime factors are 2 and 3. The lowest power of 2 is 2², and the lowest power of 3 is 3². Therefore, the GCD(252, 360) = 2² x 3² = 4 x 9 = 36.
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of all the given numbers. Using prime factorization, we take all the prime factors (from all numbers) raised to their highest power and multiply them together.
For the same numbers, 252 and 360:
- 252 = 2² x 3² x 7
- 360 = 2³ x 3² x 5
The prime factors are 2, 3, 5, and 7. The highest power of 2 is 2³, the highest power of 3 is 3², the highest power of 5 is 5¹, and the highest power of 7 is 7¹. Therefore, the LCM(252, 360) = 2³ x 3² x 5 x 7 = 8 x 9 x 5 x 7 = 2520.
Advanced Concepts Related to Prime Factorization
Understanding prime factorization opens doors to more advanced concepts in number theory:
-
Modular Arithmetic: This system deals with remainders after division. Prime numbers play a crucial role in modular arithmetic, particularly in cryptography.
-
Fermat's Little Theorem: This theorem provides a relationship between a prime number and integers not divisible by that prime. It's widely used in primality testing.
-
Chinese Remainder Theorem: This theorem helps solve systems of congruences, which are equations involving modular arithmetic. It finds applications in cryptography and other areas of computer science.
-
Prime Number Theorem: This theorem provides an approximation of the number of primes less than a given number. It's a significant result in analytic number theory.
Frequently Asked Questions (FAQ)
Q: Why is the prime factorization of a number unique?
A: The uniqueness of prime factorization is guaranteed by the Fundamental Theorem of Arithmetic. It's a fundamental property of integers.
Q: Are there infinitely many prime numbers?
A: Yes, this has been proven mathematically. Euclid's proof of the infinitude of primes is a classic example.
Q: What are some efficient algorithms for prime factorization?
A: There are various algorithms, some more efficient than others, depending on the size of the number being factored. Examples include trial division, Pollard's rho algorithm, and the general number field sieve.
Q: How does prime factorization relate to cryptography?
A: Many modern encryption methods rely on the difficulty of factoring very large numbers into their prime components. The computational cost of factoring large numbers forms the basis of the security of these systems.
Conclusion
The prime factorization of 252, while seemingly a simple exercise, reveals the depth and significance of prime numbers and their role in mathematics. Understanding this process lays the groundwork for exploring more complex concepts in number theory, cryptography, and computer science. The unique and fundamental nature of prime factorization makes it a cornerstone of mathematical understanding, impacting various fields far beyond simple arithmetic. Through its application in diverse areas, the seemingly basic concept of prime factorization demonstrates the interconnectedness and elegance of mathematics. Remember to practice, explore, and enjoy the journey of mathematical discovery!
Latest Posts
Latest Posts
-
5 Letter Word Start Sa
Sep 12, 2025
-
Prime Factor Tree Of 66
Sep 12, 2025
-
Area Of A Rectilinear Shape
Sep 12, 2025
-
A Level Biology Cell Membrane
Sep 12, 2025
-
Where Does Alum Come From
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Decomposition Of 252 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.