Prime Factor Tree For 126
elan
Sep 11, 2025 · 5 min read
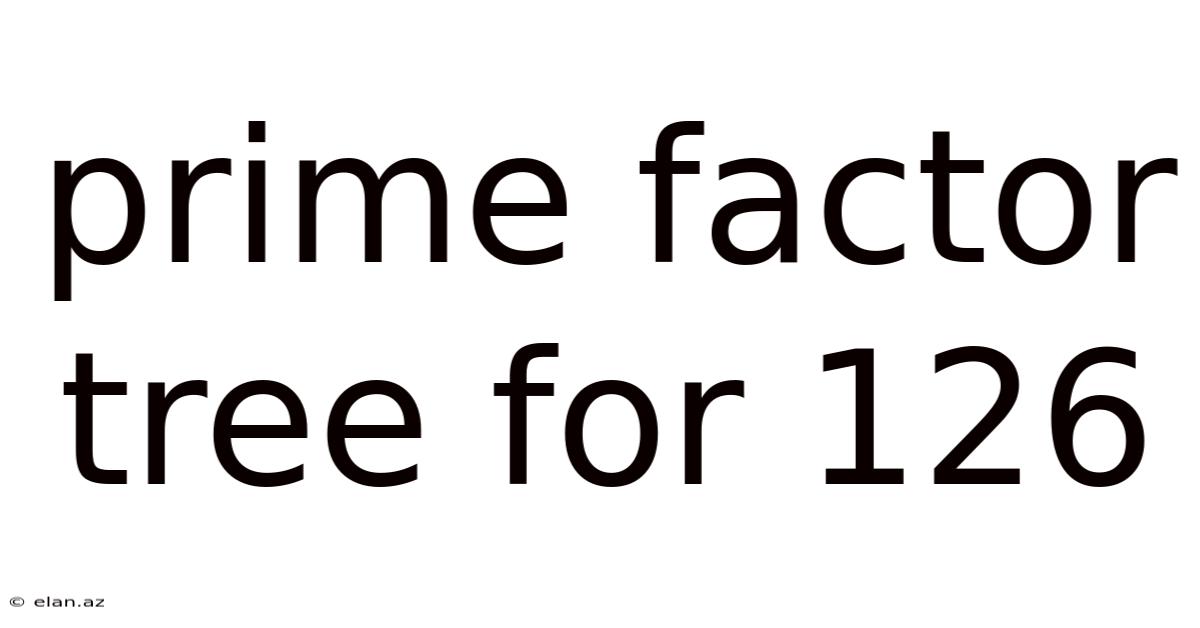
Table of Contents
Unveiling the Prime Factors of 126: A Deep Dive into Prime Factorization Using Factor Trees
Finding the prime factors of a number might seem like a dry mathematical exercise, but it's a fundamental concept with far-reaching applications in number theory, cryptography, and even computer science. This article will guide you through the process of prime factorization, specifically focusing on the number 126, using the visually intuitive method of the prime factor tree. We'll explore the concept of prime numbers, the logic behind factor trees, and delve into the significance of this seemingly simple process. By the end, you'll not only understand how to find the prime factors of 126 but also gain a deeper appreciation for the elegance and power of prime factorization.
Understanding Prime Numbers and Prime Factorization
Before we embark on our journey to factorize 126, let's refresh our understanding of some key terms. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. A number that is not prime is called a composite number. Every composite number can be expressed as a unique product of prime numbers. This is known as the Fundamental Theorem of Arithmetic, a cornerstone of number theory. The process of breaking down a composite number into its prime factors is called prime factorization.
Constructing a Prime Factor Tree for 126
The prime factor tree is a visual tool that helps us systematically decompose a number into its prime factors. Let's build one for 126:
-
Start with the number: Begin by writing the number 126 at the top of your tree.
-
Find a pair of factors: Identify two numbers that multiply to give 126. There are several possibilities (e.g., 2 x 63, 3 x 42, 6 x 21, 7 x 18, 9 x 14). Let's choose 2 and 63 for this example. Write these factors as branches extending down from 126.
-
Continue factoring: Now, we examine each of the factors (2 and 63). 2 is a prime number, so we circle it. 63, however, is a composite number. We need to find its factors. 63 can be factored into 7 and 9. Add these as branches extending down from 63.
-
Keep going until all factors are prime: 7 is a prime number, so we circle it. 9 is composite, and it factors into 3 and 3. Both 3s are prime, so we circle them.
-
Read the prime factors: Once all the branches end in circled prime numbers, we've reached the end of our prime factor tree. The prime factors of 126 are the numbers encircled at the end of each branch: 2, 3, 3, and 7.
Here's a visual representation of the prime factor tree for 126:
126
/ \
2 63
/ \
7 9
/ \
3 3
Therefore, the prime factorization of 126 is 2 x 3 x 3 x 7, or 2 x 3² x 7.
Different Paths, Same Destination: Exploring Alternative Factor Trees
It's important to note that there are multiple ways to construct a prime factor tree for a given number. The choice of factors at each step doesn't affect the final result. For instance, we could have started by factoring 126 as 3 x 42. Let's explore that path:
126
/ \
3 42
/ \
2 21
/ \
3 7
This tree yields the same prime factors: 2, 3, 3, and 7. This reinforces the Fundamental Theorem of Arithmetic—the prime factorization is unique, regardless of the path taken in the factor tree.
The Significance of Prime Factorization
Prime factorization might seem like a purely mathematical exercise, but it has significant implications in various fields:
-
Cryptography: Many modern encryption methods rely on the difficulty of factoring very large numbers into their prime factors. The security of online transactions and sensitive data often depends on this computational challenge.
-
Number Theory: Prime factorization forms the basis for numerous theorems and concepts in number theory, a branch of mathematics concerned with the properties of numbers.
-
Computer Science: Algorithms for prime factorization are crucial in various computer science applications, including cryptography and data analysis.
-
Simplifying Fractions: Prime factorization is essential for simplifying fractions to their lowest terms. By finding the common factors between the numerator and denominator, we can reduce the fraction.
-
Finding the Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Prime factorization provides an efficient method for finding the greatest common divisor and least common multiple of two or more numbers.
Frequently Asked Questions (FAQ)
Q1: What if I choose different factors at the beginning? Will I get a different answer?
No, the Fundamental Theorem of Arithmetic guarantees that the prime factorization of a number is unique, regardless of the path you take in the factor tree. You might get a different order, but the prime factors will always be the same.
Q2: Are there any shortcuts for finding prime factors?
For smaller numbers, trial division works well. For larger numbers, more sophisticated algorithms are necessary, including the Sieve of Eratosthenes and more advanced methods used in cryptography.
Q3: Why is prime factorization important in cryptography?
Modern cryptography often relies on the difficulty of factoring very large numbers into their prime factors. This makes it computationally expensive to break the encryption, protecting sensitive information.
Q4: Can every number be expressed as a product of prime numbers?
Yes, this is the essence of the Fundamental Theorem of Arithmetic. Every composite number can be uniquely expressed as a product of prime numbers (ignoring the order of the factors).
Q5: How do I find the prime factors of a very large number?
For very large numbers, specialized algorithms and computer programs are required. Trial division becomes inefficient, and more advanced methods are needed.
Conclusion: Beyond the Branches of the Tree
This exploration of the prime factorization of 126 through the prime factor tree has revealed more than just the factors 2, 3², and 7. It has demonstrated the fundamental importance of prime numbers and the elegance of the prime factorization process. This seemingly simple mathematical concept underpins many advanced mathematical theories and practical applications in various fields, highlighting the interconnectedness of mathematical ideas and their influence on the world around us. Understanding prime factorization not only expands your mathematical knowledge but also reveals the beauty and power of numbers. Remember, every composite number holds within it a unique and fascinating prime factorization waiting to be discovered.
Latest Posts
Latest Posts
-
What Is 250ml In Litres
Sep 11, 2025
-
2000 Sq Feet In Meters
Sep 11, 2025
-
Is 150 A Square Number
Sep 11, 2025
-
What Is 300cm In Inches
Sep 11, 2025
-
4 Inch How Many Mm
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Tree For 126 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.