Prime Factor Tree For 198
elan
Sep 12, 2025 · 5 min read
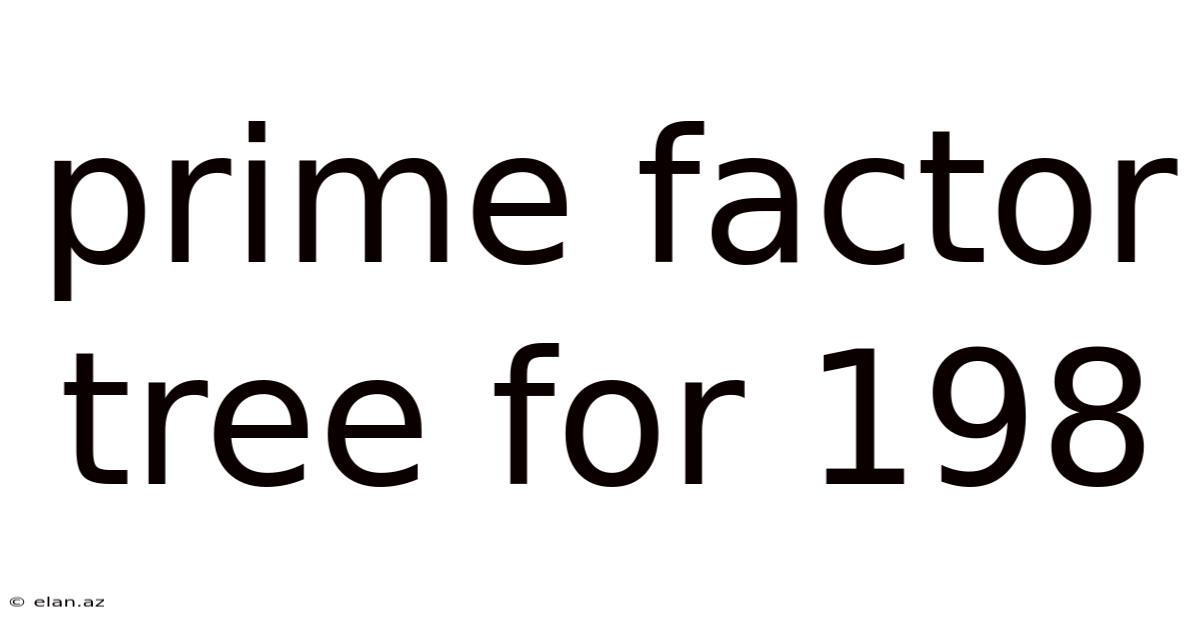
Table of Contents
Decomposing 198: A Deep Dive into Prime Factorization using the Factor Tree
Finding the prime factors of a number might seem like a dry mathematical exercise, but it's a fundamental concept with wide-ranging applications in number theory, cryptography, and even computer science. This article will guide you through the process of finding the prime factorization of 198 using a prime factor tree, explaining the method step-by-step and exploring the underlying mathematical principles. We'll also delve into why prime factorization is important and answer some frequently asked questions.
Introduction to Prime Factorization and the Factor Tree
Prime factorization is the process of breaking down a composite number (a number greater than 1 that is not prime) into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. The prime factor tree is a visual method for accomplishing this decomposition. It’s a particularly useful tool for beginners to grasp the concept. We'll use it to systematically find the prime factors of 198.
Step-by-Step Prime Factorization of 198 using a Factor Tree
Let's break down 198 into its prime factors using the factor tree method:
-
Start with the number 198 at the top of your tree. This is our starting point.
-
Find two factors of 198. We can start by noticing that 198 is an even number, so it's divisible by 2. Thus, we can write 198 as 2 x 99. Write 2 and 99 as branches stemming from 198.
-
Continue branching. Now we examine 99. It's clearly divisible by 3 (because the sum of its digits, 9+9=18, is divisible by 3). So, we branch 99 into 3 x 33. Our tree is growing!
-
Keep going until you reach prime numbers. We have 33 as a branch. 33 is also divisible by 3, giving us 3 x 11. Notice that both 3 and 11 are prime numbers.
-
The leaves are your prime factors. We've reached the end of our branching process. All the leaves at the bottom of the tree are prime numbers: 2, 3, 3, and 11.
Therefore, the prime factorization of 198 is 2 x 3 x 3 x 11, which can also be written as 2 x 3² x 11.
(Visual Representation - Imagine a tree structure here. Unfortunately, I cannot create visual diagrams in this text-based format. You can easily draw this on paper. The top would be 198, branching into 2 and 99. 99 branches into 3 and 33. Finally, 33 branches into 3 and 11. All the bottom branches (2, 3, 3, 11) are the prime factors.)
Mathematical Explanation: The Fundamental Theorem of Arithmetic
The success of the prime factorization method relies on a fundamental theorem in number theory: the Fundamental Theorem of Arithmetic. This theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This means that no matter how you approach the factorization, you will always arrive at the same set of prime factors for a given number. This uniqueness is crucial for various mathematical applications.
Alternative Methods for Finding Prime Factors
While the factor tree is visually intuitive, other methods exist for finding prime factors:
-
Division by Prime Numbers: Systematically divide the number by the smallest prime numbers (2, 3, 5, 7, 11, etc.) until you reach 1. Keep track of the prime numbers you used as divisors.
-
Using Prime Factorization Calculator: Various online tools and calculators can instantly provide the prime factorization of any number. While convenient, it's important to understand the underlying process.
The Importance of Prime Factorization
Prime factorization might seem like a purely academic exercise, but it has significant applications in various fields:
-
Cryptography: Modern encryption methods, like RSA, rely heavily on the difficulty of factoring large numbers into their prime components. The security of online transactions and sensitive data often depends on the computational challenge of prime factorization.
-
Number Theory: Prime factorization is foundational to many areas of number theory, providing insights into the structure and properties of integers.
-
Computer Science: Algorithms for prime factorization are used in various computer science applications, including data compression and efficient data storage.
-
Modular Arithmetic: Used extensively in cryptography and other fields, understanding prime factorization helps in understanding the behavior of numbers under modulo operations.
Frequently Asked Questions (FAQ)
-
Q: What if I start with different factors? Will I get a different result?
A: No. The Fundamental Theorem of Arithmetic guarantees that the prime factors will be the same, regardless of the order in which you find them. You might get a different sequence of steps in your factor tree, but the final prime factors will always be 2, 3, 3, and 11 for 198.
-
Q: Why are prime numbers important in factorization?
A: Prime numbers are the building blocks of all other integers. They cannot be broken down further into smaller whole number factors. Therefore, expressing a composite number as a product of primes provides a fundamental representation.
-
Q: How can I check if a number is prime?
A: A prime number is only divisible by 1 and itself. To check, try dividing the number by all integers from 2 up to its square root. If none of these divisions result in a whole number, the number is prime. There are more sophisticated primality tests for very large numbers.
-
Q: Is there a limit to how large a number can be prime factorized?
A: Theoretically, there's no limit. However, practically speaking, factoring extremely large numbers (hundreds or thousands of digits) is computationally very intensive and currently infeasible for even the most powerful computers, which is the cornerstone of many modern cryptographic systems.
Conclusion: Mastering Prime Factorization
Understanding prime factorization, and the use of the factor tree, is a crucial stepping stone in your mathematical journey. It's a seemingly simple concept that underlies many complex mathematical ideas and has practical applications in various fields. By mastering this technique, you'll not only improve your number sense but also gain a deeper appreciation for the fundamental structure of numbers. The example of 198 serves as a clear illustration of how to approach this valuable process, and remember that practice makes perfect! Try factoring other numbers yourself to solidify your understanding. You'll be surprised at how quickly you can become proficient.
Latest Posts
Latest Posts
-
Area Of Triangle Using Vectors
Sep 12, 2025
-
Series And Parallel Circuits Capacitors
Sep 12, 2025
-
Lcm Of 12 And 30
Sep 12, 2025
-
Profit And Loss Account Reserve
Sep 12, 2025
-
Difference Between Nationality And Citizenship
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Tree For 198 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.