Prime Factor Tree Of 42
elan
Sep 21, 2025 · 6 min read
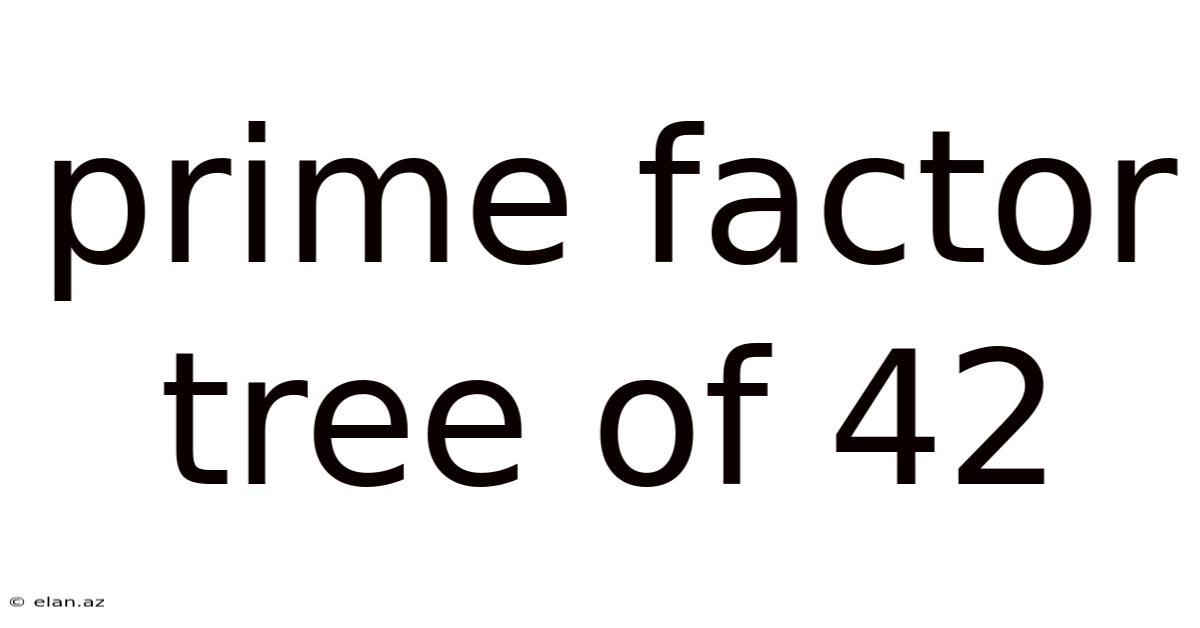
Table of Contents
Unveiling the Prime Factor Tree of 42: A Deep Dive into Number Theory
Finding the prime factors of a number might seem like a simple task, especially for smaller numbers like 42. However, understanding the process behind decomposing a number into its prime constituents is crucial for grasping fundamental concepts in number theory and algebra. This article delves into the prime factor tree of 42, explaining the method step-by-step, exploring its mathematical significance, and addressing common questions. We’ll go beyond a simple answer, examining the broader implications of prime factorization and its applications.
Introduction: What is a Prime Factor Tree?
A prime factor tree is a visual representation of the process of prime factorization. Prime factorization is the process of breaking down a composite number (a number greater than 1 that is not prime) into its prime factors – numbers that are only divisible by 1 and themselves. The prime factor tree visually organizes this process, making it easy to follow and understand. For example, understanding the prime factor tree of 42 helps illustrate how any number can be uniquely broken down into its prime building blocks. This unique representation forms the foundation for various mathematical operations and theorems.
Step-by-Step Construction of the Prime Factor Tree of 42
Let's construct the prime factor tree for 42. Remember, we're looking for the smallest prime numbers that multiply together to give us 42.
-
Start with the number 42: Write 42 at the top of your tree.
-
Find the smallest prime factor: The smallest prime number that divides 42 is 2. We write 2 as a branch below 42.
-
Divide and repeat: Divide 42 by 2, which gives us 21. Write 21 as a branch connected to the 2.
-
Continue the process: Now we find the smallest prime factor of 21, which is 3. We add a branch for 3 connected to 21.
-
Final division: Dividing 21 by 3 leaves us with 7, which is a prime number. This is our final branch.
Your completed prime factor tree should look something like this:
42
/ \
2 21
/ \
3 7
Prime Factorization of 42: The Result
By following the branches down from 42, we can see that the prime factorization of 42 is 2 x 3 x 7. This means that 2, 3, and 7 are the only prime numbers that, when multiplied together, equal 42. This is a unique factorization, meaning there's no other set of prime numbers that will produce 42. This uniqueness is guaranteed by the Fundamental Theorem of Arithmetic, a cornerstone of number theory.
The Fundamental Theorem of Arithmetic: A Cornerstone of Number Theory
The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This theorem is fundamental because it provides a unique building block representation for every integer, a property that underpins numerous concepts in higher mathematics. The prime factorization of 42 perfectly exemplifies this theorem. Its unique prime factorization (2 x 3 x 7) cannot be replicated using any other combination of prime numbers.
Applications of Prime Factorization: Beyond the Basics
While the prime factor tree of 42 might seem like a simple exercise, the concept of prime factorization has far-reaching applications in various areas of mathematics and computer science:
-
Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Finding the GCD and LCM of two or more numbers is significantly simplified using prime factorization. By comparing the prime factors of the numbers, you can easily determine their GCD (the largest number that divides all of them) and LCM (the smallest number that is divisible by all of them).
-
Cryptology and Security: Prime numbers play a crucial role in cryptography, particularly in public-key cryptography systems like RSA. These systems rely on the difficulty of factoring very large numbers into their prime factors. The security of many online transactions hinges on this computational challenge.
-
Abstract Algebra: Prime factorization is fundamental to concepts in abstract algebra, such as modular arithmetic and ring theory. These concepts form the backbone of many advanced mathematical structures.
-
Number Theory: Naturally, prime factorization is central to number theory. Research in prime numbers, distribution of primes, and related concepts are ongoing areas of study within this field.
Exploring Different Prime Factor Trees for 42
While the path we followed to create the prime factor tree resulted in 2, then 21, another equally valid approach could have started with 3 and then 14:
42
/ \
3 14
/ \
2 7
or even 7 and 6:
42
/ \
7 6
/ \
2 3
Notice that regardless of the path taken, the final prime factors remain the same: 2, 3, and 7. This reinforces the uniqueness guaranteed by the Fundamental Theorem of Arithmetic. The order of the factors doesn't matter; the final set of prime factors will always be the same.
Frequently Asked Questions (FAQ)
-
Q: Why is prime factorization important?
A: Prime factorization provides a fundamental building block representation for integers. It simplifies calculations involving GCD, LCM, and has crucial applications in cryptography and advanced mathematics.
-
Q: Is there only one way to create a prime factor tree?
A: No, there can be multiple paths to reach the same prime factorization. However, the final set of prime factors will always be the same, regardless of the path chosen.
-
Q: How do I find the prime factors of larger numbers?
A: For larger numbers, systematic methods like trial division (checking for divisibility by prime numbers in increasing order) or more advanced algorithms are used. However, the underlying principle remains the same: breaking down the number into its prime constituents.
-
Q: What if a number is already prime?
A: If a number is prime, its prime factorization is simply itself. For example, the prime factorization of 7 is just 7.
Conclusion: The Enduring Significance of Prime Factorization
The seemingly simple prime factor tree of 42 reveals a profound mathematical concept – the unique decomposition of any composite number into its prime factors. This concept, underpinned by the Fundamental Theorem of Arithmetic, is not merely an exercise in number theory; it's a foundational element that extends into various branches of mathematics, computer science, and cryptography. Understanding prime factorization, even through a simple example like 42, provides a key to unlocking deeper understanding of the structure and properties of numbers. It emphasizes that even seemingly simple mathematical concepts can reveal surprisingly profound and far-reaching implications. Therefore, exploring the prime factor tree of 42 is not just about finding the answer; it's about understanding the journey and its broader mathematical significance.
Latest Posts
Latest Posts
-
Data Representation In Computer Science
Sep 21, 2025
-
Where Does It Come From
Sep 21, 2025
-
Percentages Of An Amount Worksheet
Sep 21, 2025
-
Adding And Subtracting Fractions Worksheet
Sep 21, 2025
-
Thus Crossword Clue 3 Letters
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Tree Of 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.