Simplify 6x 8y 5x 3y
elan
Sep 16, 2025 · 6 min read
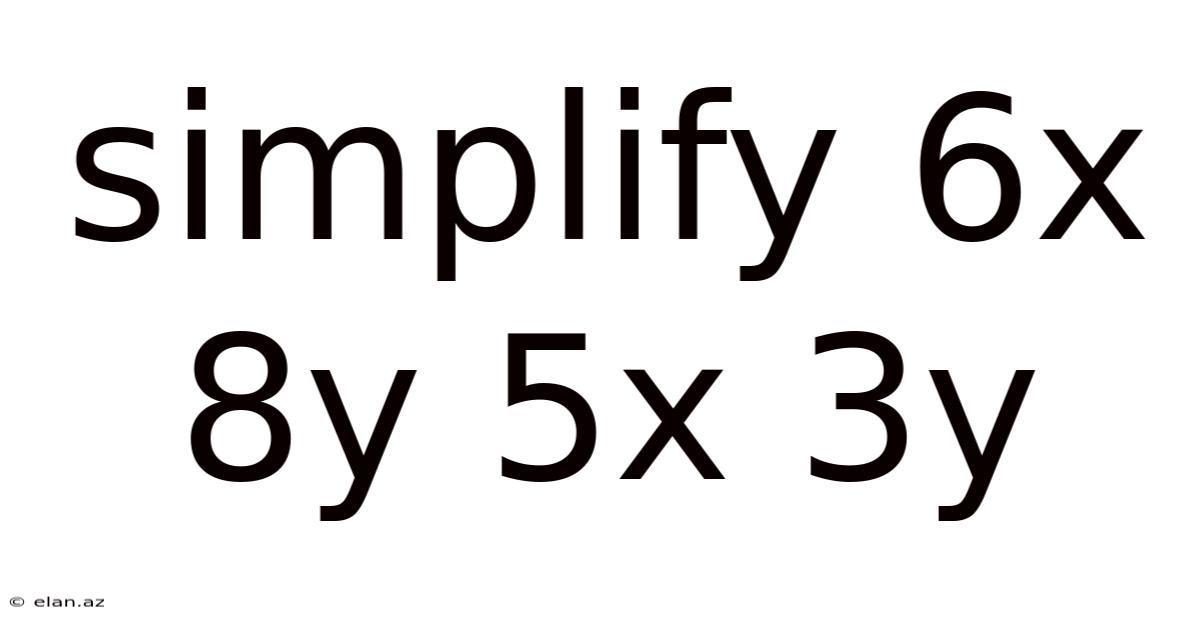
Table of Contents
Simplifying Algebraic Expressions: A Deep Dive into 6x + 8y + 5x + 3y
Understanding how to simplify algebraic expressions is a fundamental skill in mathematics, crucial for success in algebra and beyond. This comprehensive guide will walk you through the process of simplifying the expression 6x + 8y + 5x + 3y, explaining the underlying principles and providing a solid foundation for tackling more complex problems. We’ll cover the basics of algebraic expressions, delve into the concept of like terms, and demonstrate the step-by-step process of simplification, all while building your confidence and understanding.
Introduction to Algebraic Expressions
An algebraic expression is a mathematical phrase that combines numbers, variables, and operations (addition, subtraction, multiplication, and division). Variables, often represented by letters like x and y, represent unknown quantities. The expression 6x + 8y + 5x + 3y is an example of an algebraic expression containing two variables, x and y, and several terms. Each part of the expression separated by a plus or minus sign is called a term. In this case, we have four terms: 6x, 8y, 5x, and 3y.
Simplifying an algebraic expression means rewriting it in its most compact and efficient form without changing its value. This involves combining like terms, which is the core concept we'll explore next.
Understanding Like Terms
Like terms in an algebraic expression are terms that have the same variables raised to the same powers. For example:
- Like terms: 6x and 5x (both have the variable x raised to the power of 1)
- Like terms: 8y and 3y (both have the variable y raised to the power of 1)
- Unlike terms: 6x and 8y (they have different variables)
- Unlike terms: 6x and 6x² (they have the same variable but different powers)
Only like terms can be combined through addition or subtraction. This is because we are essentially counting how many of each type of variable we have. Think of it like combining apples and oranges: you can add 3 apples to 5 apples to get 8 apples, but you can't directly combine apples and oranges.
Step-by-Step Simplification of 6x + 8y + 5x + 3y
Now let's simplify the expression 6x + 8y + 5x + 3y. The process involves identifying and combining like terms:
Step 1: Identify Like Terms:
We have two sets of like terms:
- x terms: 6x and 5x
- y terms: 8y and 3y
Step 2: Combine the x terms:
To combine 6x and 5x, we add their coefficients (the numbers in front of the variable):
6x + 5x = (6 + 5)x = 11x
Step 3: Combine the y terms:
Similarly, we combine 8y and 3y by adding their coefficients:
8y + 3y = (8 + 3)y = 11y
Step 4: Write the Simplified Expression:
After combining the like terms, we have:
11x + 11y
Therefore, the simplified form of the expression 6x + 8y + 5x + 3y is 11x + 11y. This is the most concise and efficient way to represent the original expression.
Further Exploration: More Complex Algebraic Expressions
The principles we've used to simplify 6x + 8y + 5x + 3y apply to more complex algebraic expressions as well. Let's consider a few examples:
-
Example 1: 4a + 2b - a + 5b
- Identify like terms: 4a and -a; 2b and 5b
- Combine like terms: 4a - a = 3a; 2b + 5b = 7b
- Simplified expression: 3a + 7b
-
Example 2: 3x² + 5x - 2x² + x
- Identify like terms: 3x² and -2x²; 5x and x
- Combine like terms: 3x² - 2x² = x²; 5x + x = 6x
- Simplified expression: x² + 6x
-
Example 3: 7xy + 2x - 3xy + 5y
- Identify like terms: 7xy and -3xy; 2x and 5y (note that 2x and 5y are unlike terms)
- Combine like terms: 7xy - 3xy = 4xy
- Simplified expression: 4xy + 2x + 5y (cannot be simplified further because the remaining terms are unlike)
These examples highlight that the process always involves:
- Identifying Like Terms: Carefully examine the expression and group together terms with the same variables raised to the same powers.
- Combining Like Terms: Add or subtract the coefficients of the like terms, keeping the variable and its exponent unchanged.
- Writing the Simplified Expression: Combine the simplified like terms to obtain the final, simplified expression.
The Commutative Property in Simplification
The commutative property of addition states that the order of terms in an addition doesn't affect the sum. This means we can rearrange the terms in our expression to group like terms more easily before combining them. For example:
6x + 8y + 5x + 3y can be rearranged as:
6x + 5x + 8y + 3y
This rearrangement makes it easier to visually identify and combine like terms.
The Distributive Property and its Relevance
While not directly used in simplifying 6x + 8y + 5x + 3y, the distributive property is crucial when dealing with expressions involving parentheses. The distributive property states: a(b + c) = ab + ac. This means that a number or variable outside a set of parentheses multiplies each term within the parentheses. This property often comes into play when simplifying more complex expressions that include parentheses. For example:
2(x + 3y) = 2x + 6y
Common Mistakes to Avoid
- Adding Unlike Terms: This is the most common mistake. Remember, only like terms can be combined.
- Incorrectly Combining Coefficients: Double-check your addition and subtraction of coefficients.
- Ignoring Negative Signs: Pay careful attention to the signs of the terms, particularly when subtracting.
Frequently Asked Questions (FAQ)
Q1: What happens if I have more than two variables?
A1: The same principles apply. Identify like terms based on the combination of variables and their exponents. For example, in the expression 3xy + 2x + 5xy - y, you would combine 3xy and 5xy to get 8xy. The other terms (2x and -y) are unlike terms and cannot be simplified further.
Q2: What if a term has an exponent other than 1?
A2: The terms must have the exact same variable and exponent to be considered like terms. For example, 2x² and 5x are unlike terms, as are 3x and 3x³.
Q3: Can I simplify expressions with fractions or decimals?
A3: Yes, the process remains the same. You'll combine like terms by adding or subtracting their coefficients, even if those coefficients are fractions or decimals.
Q4: How do I handle expressions with parentheses?
A4: Use the distributive property to eliminate the parentheses first, then proceed with identifying and combining like terms.
Q5: What if there are no like terms?
A5: If there are no like terms, the expression is already in its simplest form.
Conclusion
Simplifying algebraic expressions is a fundamental skill in algebra and beyond. By understanding the concept of like terms and systematically combining them, you can efficiently rewrite complex expressions into their most compact forms. Mastering this skill provides a solid foundation for tackling more advanced algebraic concepts and problem-solving. Remember to practice regularly, pay attention to detail, and review the key concepts—like terms, the commutative property, and the distributive property—to solidify your understanding. With consistent effort, you'll become proficient in simplifying algebraic expressions and confidently navigate the world of algebra.
Latest Posts
Latest Posts
-
Milton Keynes Theory Test Centre
Sep 16, 2025
-
5 Letter Words Starting Me
Sep 16, 2025
-
Relating To Sight 6 Letters
Sep 16, 2025
-
150 Degrees Fahrenheit To Celsius
Sep 16, 2025
-
How Far Is 5000 Meters
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Simplify 6x 8y 5x 3y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.