Sin X Cos X Integral
elan
Sep 22, 2025 · 6 min read
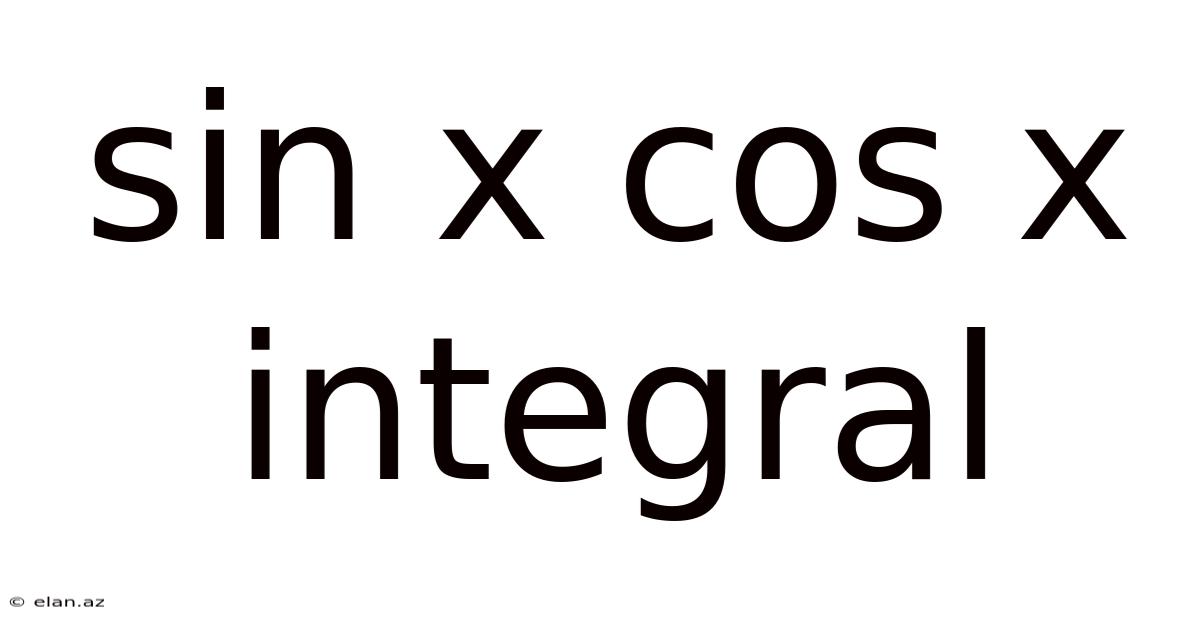
Table of Contents
Decoding the Integral of sin x cos x: A Comprehensive Guide
The integral of sin x cos x, often encountered in calculus courses and various applications of mathematics, might initially seem daunting. However, with a systematic approach and a clear understanding of trigonometric identities, this seemingly complex problem becomes quite manageable. This comprehensive guide will delve into the various methods for solving this integral, explaining the underlying principles and providing ample context for a deeper understanding. We'll explore both the direct method using trigonometric identities and the substitution method, clarifying the advantages and disadvantages of each approach.
Introduction: Why is this Integral Important?
The integral ∫sin x cos x dx appears frequently in various fields, including physics (oscillatory motion, wave mechanics), engineering (signal processing), and computer graphics (modeling curves). Mastering its solution is crucial for students progressing in their calculus journey and professionals applying calculus in their respective domains. Understanding the different techniques available to solve this integral provides a strong foundation for tackling more complex trigonometric integrals. The ability to manipulate trigonometric functions and apply appropriate integration techniques is a fundamental skill in advanced mathematics.
Method 1: Using Trigonometric Identities – The Direct Approach
This method leverages trigonometric identities to simplify the integrand before integration. The key identity we will use is the double-angle formula for sine:
sin 2x = 2 sin x cos x
Rearranging this equation, we get:
sin x cos x = (1/2) sin 2x
Now, substituting this into our integral:
∫sin x cos x dx = ∫(1/2) sin 2x dx
This integral is now straightforward to solve. We can use a simple u-substitution:
Let u = 2x, then du = 2 dx => dx = (1/2) du
Substituting these into the integral:
∫(1/2) sin 2x dx = ∫(1/2) sin u (1/2) du = (1/4) ∫sin u du
The integral of sin u is -cos u. Therefore:
(1/4) ∫sin u du = -(1/4) cos u + C
Substituting back for u = 2x, we get the final result:
∫sin x cos x dx = -(1/4) cos 2x + C
where C is the constant of integration. This is the simplest and most direct method to solve the integral.
Method 2: Integration by Substitution (u-Substitution)
While the trigonometric identity method is efficient, the substitution method offers a more general approach applicable to a wider range of trigonometric integrals. Let's explore this alternative.
We can choose either sin x or cos x as our substitution variable. Let's choose:
u = sin x
Then, du = cos x dx
Substituting these into the integral:
∫sin x cos x dx = ∫u du
This is a simple power rule integral:
∫u du = (1/2)u² + C
Substituting back u = sin x, we get:
∫sin x cos x dx = (1/2) sin²x + C
This result might seem different from the result obtained using the trigonometric identity. However, it's important to remember that these two results are equivalent. Let's demonstrate this using the double-angle formula for cosine:
cos 2x = 1 - 2sin²x = 2cos²x -1
From the first part of the equation, we can solve for sin²x:
sin²x = (1 - cos 2x)/2
Substituting this into our result from the u-substitution:
(1/2) sin²x + C = (1/2) [(1 - cos 2x)/2] + C = (1/4)(1 - cos 2x) + C = (1/4) - (1/4)cos 2x + C
Since C is an arbitrary constant, (1/4) + C can be replaced by another arbitrary constant, say C'. Therefore, we get:
(1/2) sin²x + C = -(1/4) cos 2x + C'
This confirms that both methods yield equivalent results, differing only by a constant of integration.
Method 3: Another Substitution Approach
Alternatively, we could have chosen u = cos x. Then du = -sin x dx, and the integral becomes:
∫sin x cos x dx = ∫-u du = -(1/2)u² + C = -(1/2)cos²x + C
Again, this result appears different but is equivalent to the previous results. Using the double-angle formula for cosine (cos 2x = 2cos²x - 1), we can show the equivalence:
-(1/2)cos²x + C = -(1/2)[(1 + cos 2x)/2] + C = -(1/4)(1 + cos 2x) + C = -(1/4) - (1/4)cos 2x + C
Again, absorbing -(1/4) into the constant of integration, we obtain a result equivalent to the others.
Explanation of the Different Results and the Constant of Integration (C)
The appearance of different results from different integration methods might seem confusing, but it's entirely expected. The constant of integration, C, is arbitrary. It represents an infinite family of functions whose derivatives are the same. Each method provides a valid representation within this family. The differences are absorbed by the constant of integration, which can take on different values depending on the chosen method and the initial conditions.
Illustrative Examples
Let's consider some examples to solidify our understanding.
Example 1: Find the definite integral of sin x cos x from 0 to π/2.
Using the result -(1/4)cos 2x + C:
∫₀^(π/2) sin x cos x dx = [-(1/4)cos 2x]₀^(π/2) = -(1/4)cos π - [-(1/4)cos 0] = (1/4) + (1/4) = 1/2
Using the result (1/2)sin²x + C:
∫₀^(π/2) sin x cos x dx = [(1/2)sin²x]₀^(π/2) = (1/2)sin²(π/2) - (1/2)sin²(0) = (1/2) - 0 = 1/2
Example 2: Find the indefinite integral of 2 sin x cos x.
This is simply twice the integral we've been solving:
∫2 sin x cos x dx = 2∫sin x cos x dx = 2[-(1/4)cos 2x + C] = -(1/2)cos 2x + 2C = -(1/2)cos 2x + C' (where C' = 2C)
Notice how the constant of integration still remains arbitrary.
Frequently Asked Questions (FAQs)
-
Q: Which method is best for solving ∫sin x cos x dx?
- A: The method using the double-angle formula (sin 2x = 2sin x cos x) is generally the most efficient and straightforward. However, understanding substitution methods is crucial for tackling more complex integrals.
-
Q: Why do different methods produce seemingly different results?
- A: The apparent differences are due to the arbitrary constant of integration. All methods yield results that are equivalent up to a constant.
-
Q: Can I use other trigonometric identities to solve this integral?
- A: While the double-angle formula is most convenient, other identities could be used, but they would likely lead to more complex calculations.
Conclusion:
Solving the integral of sin x cos x demonstrates the power of trigonometric identities and substitution techniques in integration. While several approaches exist, all lead to equivalent solutions, differing only by the arbitrary constant of integration. Mastering these methods is essential for building a robust foundation in calculus and its diverse applications. Remember to choose the method that best suits your understanding and the specific context of the problem. The key takeaway is the understanding of the underlying principles rather than merely memorizing a single solution. This comprehensive exploration of the integral of sin x cos x provides a solid framework for tackling more complex trigonometric integrals in the future. The ability to skillfully manipulate trigonometric functions and apply integration techniques effectively is a cornerstone of mathematical proficiency.
Latest Posts
Latest Posts
-
Letter Of Permission To Travel
Sep 22, 2025
-
Going Through The Motions Meaning
Sep 22, 2025
-
5 Letter Word Ending On
Sep 22, 2025
-
Are Interviews Qualitative Or Quantitative
Sep 22, 2025
-
What Is A Secondary Sector
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Sin X Cos X Integral . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.