What Is 2/5 As Decimal
elan
Sep 16, 2025 · 5 min read
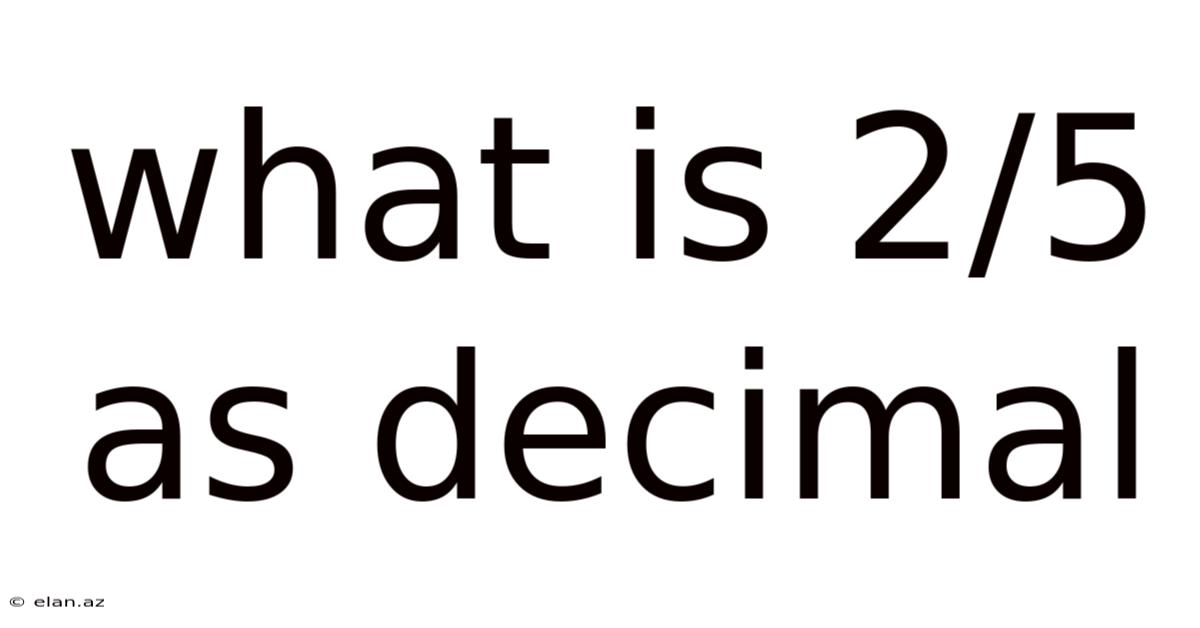
Table of Contents
What is 2/5 as a Decimal? A Comprehensive Guide
Fractions and decimals are fundamental concepts in mathematics, representing parts of a whole. Understanding how to convert between these two forms is crucial for various mathematical operations and real-world applications. This article provides a comprehensive guide to converting the fraction 2/5 into its decimal equivalent, exploring different methods and delving into the underlying mathematical principles. We'll also cover related concepts to ensure a solid understanding of fractional and decimal representation.
Understanding Fractions and Decimals
Before diving into the conversion of 2/5, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we have 2 parts out of a total of 5 equal parts.
A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). Decimals are written using a decimal point (.), separating the whole number part from the fractional part. For example, 0.5 represents 5/10, and 0.25 represents 25/100.
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. To convert 2/5 to a decimal, we simply divide the numerator (2) by the denominator (5):
2 ÷ 5 = 0.4
Therefore, 2/5 as a decimal is 0.4. This method works for any fraction; simply divide the numerator by the denominator.
Method 2: Equivalent Fractions
Another way to convert 2/5 to a decimal involves creating an equivalent fraction with a denominator that is a power of 10. We want to find a number that, when multiplied by 5, results in a power of 10. In this case, multiplying 5 by 2 gives us 10:
2/5 * 2/2 = 4/10
Since 4/10 represents 4 parts out of 10, we can easily express this as a decimal: 0.4. This method highlights the relationship between fractions and decimals, showing how they represent the same value in different forms.
Method 3: Understanding Place Value
Decimals represent fractions based on powers of 10. The first digit after the decimal point represents tenths (1/10), the second digit represents hundredths (1/100), and so on. Understanding place value allows us to directly convert some fractions to decimals.
In the case of 2/5, we know that 1/5 is equal to 2/10 or 0.2. Therefore, 2/5 is simply twice this value: 2 * 0.2 = 0.4.
Expanding on the Concept: Converting Other Fractions to Decimals
The methods described above can be applied to a wide range of fractions. However, some fractions result in repeating decimals (decimals with a pattern that repeats infinitely) or terminating decimals (decimals that end after a finite number of digits).
Terminating Decimals: These occur when the denominator of the fraction contains only factors of 2 and/or 5. For example:
- 1/2 = 0.5
- 3/4 = 0.75
- 7/10 = 0.7
- 25/100 = 0.25
Repeating Decimals: These occur when the denominator of the fraction contains prime factors other than 2 and 5. For example:
- 1/3 = 0.3333... (the 3 repeats infinitely)
- 2/7 = 0.285714285714... (the sequence 285714 repeats infinitely)
To represent repeating decimals, we often use a bar over the repeating digits. For example, 1/3 is written as 0.3̅.
Practical Applications of Decimal Conversions
Converting fractions to decimals is crucial in various real-world scenarios:
- Finance: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals.
- Measurement: Converting units of measurement, such as inches to centimeters or ounces to grams, often requires decimal conversions.
- Science: Representing experimental data and performing calculations in scientific fields often involves decimals.
- Engineering: Precise calculations in engineering designs and construction often utilize decimal values.
Further Exploration: Working with Mixed Numbers
A mixed number combines a whole number and a fraction (e.g., 1 2/5). To convert a mixed number to a decimal, first convert the fractional part to a decimal, then add the whole number.
For example, to convert 1 2/5 to a decimal:
- Convert the fraction 2/5 to a decimal: 0.4
- Add the whole number: 1 + 0.4 = 1.4
Therefore, 1 2/5 as a decimal is 1.4.
Frequently Asked Questions (FAQ)
Q1: What is the simplest way to convert 2/5 to a decimal?
A1: The simplest method is direct division: 2 ÷ 5 = 0.4
Q2: Can all fractions be converted to terminating decimals?
A2: No, only fractions whose denominators have only 2 and/or 5 as prime factors result in terminating decimals. Other fractions will result in repeating decimals.
Q3: How do I convert a fraction with a large denominator to a decimal?
A3: Use long division. Divide the numerator by the denominator. For very large numbers, a calculator can be helpful.
Q4: What is the difference between a fraction and a decimal?
A4: A fraction expresses a part of a whole as a ratio of two numbers (numerator/denominator). A decimal expresses a part of a whole using base-10 notation, with digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on.
Q5: Why is understanding decimal conversion important?
A5: Decimal conversions are essential for numerous applications across various fields, including finance, science, engineering, and everyday calculations. They provide a more convenient format for many calculations compared to fractions.
Conclusion
Converting fractions to decimals is a fundamental skill in mathematics with widespread applications. We have explored various methods for converting 2/5 to its decimal equivalent (0.4), including direct division, equivalent fractions, and understanding place value. We have also touched upon converting other fractions, including those resulting in repeating decimals, and the conversion of mixed numbers. Understanding these methods and their underlying principles will provide a solid foundation for further mathematical studies and real-world problem-solving. By mastering these techniques, you'll enhance your mathematical fluency and confidence in tackling various numerical challenges.
Latest Posts
Latest Posts
-
Kathak Dance Classes Near Me
Sep 16, 2025
-
Best Pillow For Neck Honeydewsleep
Sep 16, 2025
-
Minimum Point Of A Curve
Sep 16, 2025
-
Diagram Of A Plant Labelled
Sep 16, 2025
-
What Does Ws Stand For
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/5 As Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.