What Is 2/5 Of 24
elan
Sep 20, 2025 · 5 min read
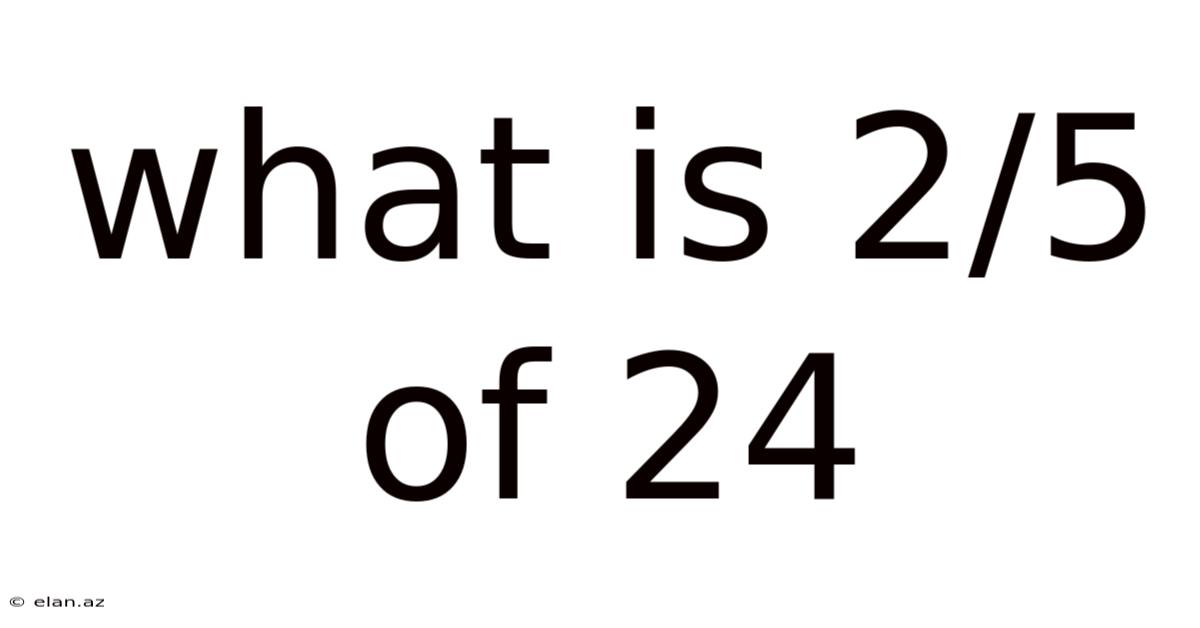
Table of Contents
What is 2/5 of 24? A Deep Dive into Fractions and Their Applications
Finding 2/5 of 24 might seem like a simple arithmetic problem, easily solved with a calculator. However, understanding the underlying concepts of fractions and their application extends far beyond a simple numerical answer. This article delves into the meaning of fractions, explores different methods for solving this specific problem, and expands upon the broader applications of fractional calculations in various fields. We'll unpack the process step-by-step, ensuring a comprehensive understanding for learners of all levels. This will cover everything from the basic mathematical operations to real-world examples showcasing the practical utility of fractional calculations.
Understanding Fractions: A Foundation for Calculation
Before we tackle the problem of finding 2/5 of 24, let's establish a firm grasp on the fundamental concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator shows the total number of equal parts the whole is divided into.
In the fraction 2/5, '2' is the numerator and '5' is the denominator. This means we are considering 2 out of 5 equal parts of a whole. Understanding this representation is crucial for performing any calculations involving fractions.
Method 1: Multiplication of Fractions and Whole Numbers
The most straightforward approach to finding 2/5 of 24 is to convert the whole number 24 into a fraction. Any whole number can be expressed as a fraction by placing it over 1. Therefore, 24 can be written as 24/1.
Now, we multiply the two fractions:
(2/5) * (24/1) = (2 * 24) / (5 * 1) = 48/5
This result, 48/5, is an improper fraction because the numerator is larger than the denominator. To convert it to a mixed number (a whole number and a fraction), we perform division:
48 ÷ 5 = 9 with a remainder of 3.
Therefore, 48/5 is equal to 9 3/5. So, 2/5 of 24 is 9 3/5.
Method 2: Finding the Fractional Part and Multiplying
Another approach involves breaking down the problem into smaller steps. First, we find 1/5 of 24 by dividing 24 by 5:
24 ÷ 5 = 4.8
Since we want 2/5, we multiply this result by 2:
4.8 * 2 = 9.6
Therefore, 2/5 of 24 is 9.6. Note that this method yields a decimal answer, which is equivalent to the mixed number 9 3/5 obtained in Method 1 (9.6 = 9 + 0.6 = 9 + 3/5).
Method 3: Visual Representation and Understanding
Visual aids can be particularly helpful in grasping the concept of fractions, especially for beginners. Imagine a rectangular pizza divided into 5 equal slices. Finding 2/5 of the pizza means taking 2 out of these 5 slices. If the whole pizza represents 24, each slice represents 24/5 = 4.8. Taking two slices would give us 2 * 4.8 = 9.6. This visual representation reinforces the understanding of the fractional calculation.
Expanding the Concept: Real-World Applications of Fractional Calculations
The calculation of 2/5 of 24, while seemingly simple, highlights the widespread applicability of fractional calculations in everyday life and various professional fields. Here are a few examples:
-
Cooking and Baking: Recipes often require fractional measurements. For example, a recipe might call for 2/3 cup of flour or 1/2 teaspoon of baking powder. Understanding fractions is essential for accurate measurements and successful cooking.
-
Finance and Budgeting: Fractions are crucial in managing personal finances. Calculating discounts (e.g., 2/5 off the original price), understanding interest rates (expressed as fractions or percentages), and budgeting (allocating a fraction of income to different expenses) all require fractional calculations.
-
Construction and Engineering: Precision is paramount in construction and engineering. Blueprints and designs frequently incorporate fractional measurements for accurate construction and material calculations. Fractional calculations ensure the structural integrity and functionality of buildings and infrastructure.
-
Data Analysis and Statistics: Fractions and percentages are indispensable tools in data analysis and statistics. Representing proportions, calculating probabilities, and interpreting data frequently involve fractions.
-
Science and Research: Many scientific formulas and measurements utilize fractions. In chemistry, for instance, understanding molar ratios (represented as fractions) is essential for accurate chemical reactions.
Frequently Asked Questions (FAQs)
Q1: Can I use a calculator to solve this problem?
A1: Yes, absolutely. Calculators can simplify the process, especially when dealing with more complex fractions or larger numbers. Simply enter 2/5 * 24 into your calculator to obtain the answer 9.6.
Q2: Why are there two different answers (9 3/5 and 9.6)?
A2: Both answers are correct and represent the same value. 9 3/5 is a mixed number, while 9.6 is its decimal equivalent. The choice of representation depends on the context and desired level of precision.
Q3: What if the fraction was a larger number, like 27/50 of 24?
A3: The same principles apply. You would multiply (27/50) * (24/1) and simplify the resulting fraction. The process might be more involved, but the fundamental steps remain the same.
Q4: How can I improve my understanding of fractions?
A4: Practice is key! Work through various examples, try different methods of solving problems, and use visual aids to enhance your understanding. Online resources, educational videos, and textbooks can provide further assistance.
Conclusion: Beyond the Numbers
Finding 2/5 of 24 is more than just a simple mathematical calculation. It's a gateway to understanding the broader concept of fractions, their diverse applications, and their importance in numerous fields. By mastering fractional calculations, we equip ourselves with essential tools for problem-solving in various aspects of life, from everyday tasks to complex professional endeavors. Remember, the journey to mastering fractions is about understanding the underlying principles and building confidence in applying those principles to real-world scenarios. Consistent practice and a curious mind will pave the way for success. Don't be afraid to explore different methods and seek clarification when needed—the power of fractions lies not just in the answer, but in the process of understanding how to arrive at it.
Latest Posts
Latest Posts
-
Cross Section Of A Prism
Sep 20, 2025
-
How Big Is 13 Inches
Sep 20, 2025
-
Is English Difficult To Learn
Sep 20, 2025
-
Addition And Subtraction Year 2
Sep 20, 2025
-
Image Of An Animal Cell
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/5 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.