What Is 20 Of 65.00
elan
Sep 20, 2025 · 5 min read
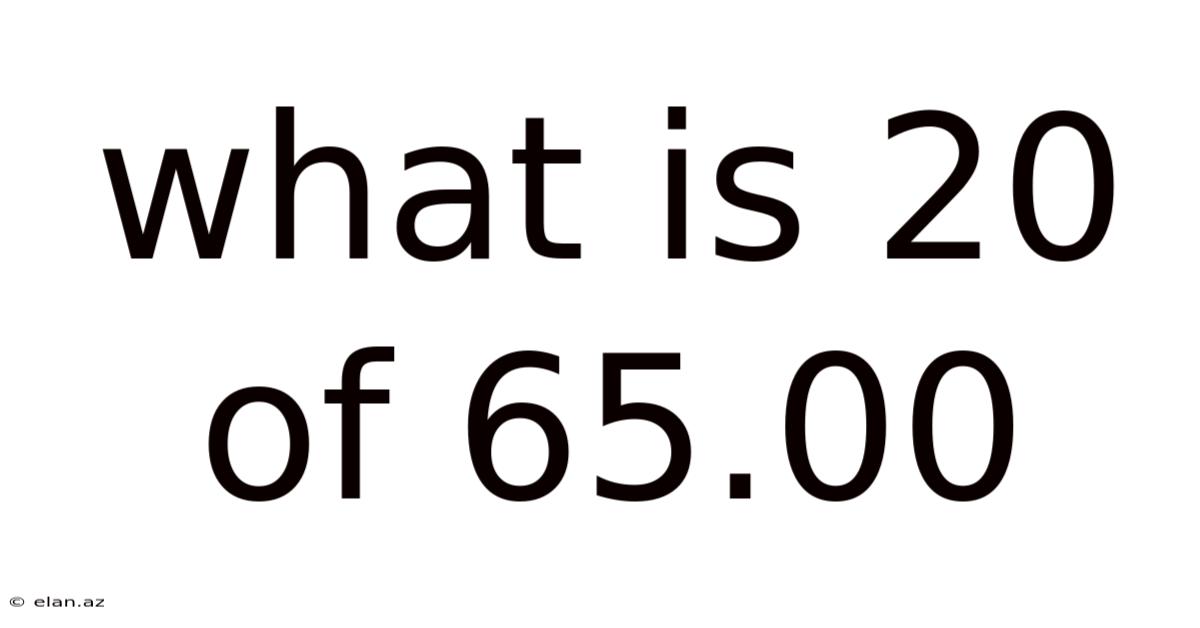
Table of Contents
What is 20% of 65.00? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts and taxes to comprehending financial reports and statistical data. This article will not only answer the question, "What is 20% of 65.00?" but also provide a comprehensive understanding of percentages, their calculations, and their real-world applications. We'll explore different methods for solving percentage problems, ensuring you gain a solid grasp of this important mathematical concept.
Introduction: Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). We use the symbol "%" to represent percentages. For example, 20% means 20 out of 100, which can be written as the fraction 20/100 or the decimal 0.20.
Calculating 20% of 65.00: Three Approaches
There are several ways to calculate 20% of 65.00. Let's explore three common methods:
1. Using the Decimal Method:
This is often the most straightforward approach. First, convert the percentage to a decimal by dividing it by 100. 20% divided by 100 is 0.20. Then, multiply the decimal by the number you want to find the percentage of:
0.20 * 65.00 = 13.00
Therefore, 20% of 65.00 is $\boxed{13.00}$.
2. Using the Fraction Method:
Percentages can also be expressed as fractions. 20% can be written as 20/100, which simplifies to 1/5. To find 20% of 65.00, multiply 65.00 by the fraction 1/5:
(1/5) * 65.00 = 13.00
Again, we find that 20% of 65.00 is $\boxed{13.00}$.
3. Using the Proportion Method:
This method sets up a proportion to solve for the unknown value. We can set up the proportion as follows:
20/100 = x/65.00
Where 'x' represents the unknown value (20% of 65.00). To solve for 'x', we cross-multiply:
20 * 65.00 = 100 * x
1300 = 100x
x = 1300 / 100
x = 13.00
Once again, we arrive at the answer: 20% of 65.00 is $\boxed{13.00}$.
Beyond the Calculation: Real-World Applications of Percentages
The ability to calculate percentages is crucial in many real-world situations. Here are some examples:
-
Sales and Discounts: Stores frequently offer discounts expressed as percentages. Understanding percentages allows you to quickly calculate the final price after a discount. For instance, a 20% discount on a $65.00 item means you'll save $13.00, resulting in a final price of $52.00.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Knowing how to calculate percentages helps you determine the amount of tax you'll owe.
-
Tips and Gratuities: When dining out, it's customary to leave a tip, usually expressed as a percentage of the bill. Calculating a 15% or 20% tip accurately demonstrates good etiquette and financial awareness.
-
Interest Rates: Understanding interest rates (often expressed as annual percentages) is essential for managing personal finances, especially when dealing with loans, savings accounts, and investments. The ability to calculate compound interest is a valuable financial skill.
-
Financial Statements: Financial reports for businesses and individuals often utilize percentages to show ratios, changes over time, and other important financial metrics. Understanding percentages enables informed financial decision-making.
-
Statistics and Data Analysis: Percentages are widely used in statistics to represent proportions, probabilities, and trends in data. This is vital in fields such as research, market analysis, and public health.
-
Grade Calculation: In many educational settings, final grades are calculated using percentages of various assessment components (e.g., homework, quizzes, exams).
Further Exploration: Advanced Percentage Calculations
While calculating a simple percentage like 20% of 65.00 is relatively straightforward, more complex percentage problems can arise. Here are some examples:
-
Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two values. For example, if a stock price increases from $50 to $60, the percentage increase can be calculated as follows:
[(60 - 50) / 50] * 100% = 20%
-
Finding the Original Value: Suppose you know the final value after a percentage increase or decrease, and you want to find the original value. This often requires working backward using algebraic equations.
-
Calculating Compound Interest: Compound interest involves calculating interest not only on the principal amount but also on accumulated interest. This requires iterative calculations and understanding exponential growth.
-
Working with Multiple Percentages: Some problems may involve applying multiple percentages sequentially or combining percentages. This requires careful attention to order of operations and understanding the cumulative effect.
Frequently Asked Questions (FAQs)
-
What if I need to calculate a percentage that isn't a whole number, like 12.5%? You can use the same methods described above, simply converting the percentage to a decimal (0.125) or fraction (1/8) before multiplying.
-
What are some common percentage shortcuts? Knowing that 10% of a number is simply that number divided by 10 can help streamline calculations. You can then use this to calculate other percentages based on multiples or fractions of 10%. For example, 5% is half of 10%, and 20% is double 10%.
-
Are there any online calculators for percentages? Yes, many websites and apps provide percentage calculators to assist with various percentage calculations. These calculators can be useful for checking your work or for more complex problems.
-
How can I improve my skills in calculating percentages? Practice is key. Work through various problems, starting with simple examples and gradually moving to more complex ones. Use different calculation methods to build your understanding and identify your preferred approach.
Conclusion: Mastering Percentages – A Valuable Life Skill
The ability to accurately and efficiently calculate percentages is a fundamental mathematical skill with widespread applications in everyday life and various professional fields. By understanding the different methods for calculating percentages, as demonstrated through the example of finding 20% of 65.00, you equip yourself with a valuable tool for navigating numerous situations, from managing personal finances to understanding complex data. Continuous practice and exploration of more advanced percentage calculations will further solidify this crucial skill and enhance your quantitative reasoning abilities. Remember, understanding percentages isn't just about numbers; it's about empowering yourself to make informed decisions in various aspects of your life.
Latest Posts
Latest Posts
-
200 Cm How Many Inches
Sep 20, 2025
-
Grammar Subject Verb Agreement Worksheet
Sep 20, 2025
-
Integration A Level Maths Questions
Sep 20, 2025
-
Nth Term Of Linear Sequences
Sep 20, 2025
-
To Make Square Or Rectangular
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 65.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.