What Is 25 Of 90
elan
Sep 20, 2025 · 5 min read
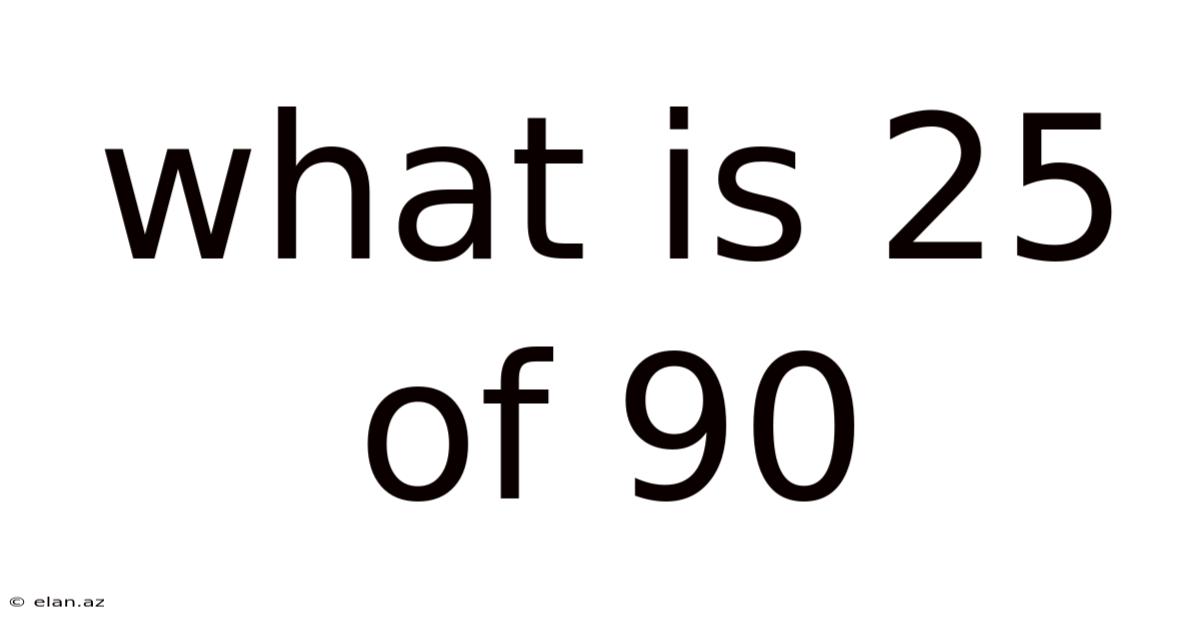
Table of Contents
What is 25% of 90? A Deep Dive into Percentages and Their Applications
Finding 25% of 90 might seem like a simple arithmetic problem, easily solved with a calculator. However, understanding the underlying principles of percentages and their diverse applications extends far beyond this basic calculation. This article will not only show you how to calculate 25% of 90 but will also delve into the meaning of percentages, various calculation methods, real-world examples, and address frequently asked questions. By the end, you'll possess a comprehensive understanding of percentages and their importance in various fields.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Therefore, 25% represents 25 out of 100, or 25/100, which simplifies to 1/4. This fractional representation is crucial for understanding the core concept. Percentages are used extensively to express proportions, ratios, rates of change, and probabilities in various contexts.
Calculating 25% of 90: Three Methods
There are several ways to calculate 25% of 90. Let's explore three common methods:
Method 1: Using the Fractional Equivalent
As mentioned earlier, 25% is equivalent to 1/4. Therefore, finding 25% of 90 is the same as finding 1/4 of 90. This can be calculated as:
(1/4) * 90 = 90 / 4 = 22.5
Method 2: Converting Percentage to Decimal
To convert a percentage to a decimal, divide the percentage by 100. Therefore, 25% becomes 25/100 = 0.25. Then, multiply this decimal by 90:
0.25 * 90 = 22.5
Method 3: Using Proportions
We can set up a proportion to solve this:
25/100 = x/90
To solve for x (25% of 90), cross-multiply:
25 * 90 = 100 * x
2250 = 100x
x = 2250 / 100 = 22.5
Real-World Applications of Percentages
The application of percentages extends to numerous fields, including:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all involve percentages. For example, a 25% discount on a $90 item would result in a savings of $22.50.
-
Statistics: Percentages are essential for representing data in charts, graphs, and tables. They are crucial for summarizing and comparing datasets, illustrating trends, and making inferences. For instance, if 25% of a population prefers a certain product, it reveals crucial market insights.
-
Science: Percentages are used to express concentrations of solutions, error margins in experiments, and changes in quantities. In chemistry, for example, a 25% solution of a particular chemical would indicate its concentration relative to the total volume.
-
Education: Grades are often expressed as percentages, and progress tracking in education frequently employs percentage-based metrics to assess student performance and learning outcomes.
-
Everyday Life: From calculating tips in restaurants to understanding sales tax, percentages are integral parts of our daily financial transactions.
Beyond the Basics: Advanced Percentage Calculations
While calculating 25% of 90 is straightforward, understanding more complex percentage problems is crucial. Here are some examples:
-
Finding the Percentage: If you bought a shirt for $22.50 and it was discounted from its original price of $90, what percentage discount did you get? This involves calculating (90 - 22.5) / 90 * 100% = 75%.
-
Percentage Increase/Decrease: Suppose the price of an item increased from $90 to $112.50. To calculate the percentage increase, find the difference ($112.50 - $90 = $22.50), divide by the original price ($22.50 / $90), and multiply by 100% to get a 25% increase.
-
Compound Interest: Compound interest calculations involve repeated percentage additions, making them more complex but crucial in finance and investment understanding.
-
Percentage Points vs. Percentages: It's important to differentiate between percentage points and percentages. A change from 25% to 50% is a 25 percentage point increase, but it represents a 100% increase relative to the initial value.
Practical Exercises
To solidify your understanding, try these exercises:
- What is 15% of 60?
- What percentage is 18 out of 72?
- A store offers a 30% discount on a $150 item. What is the final price?
- If the population of a town increased from 5000 to 6250, what is the percentage increase?
Frequently Asked Questions (FAQ)
Q: Why are percentages useful?
A: Percentages provide a standardized way to compare proportions and ratios, making them easily understandable and comparable across different contexts. They simplify complex numerical relationships.
Q: Can I use a calculator for percentage calculations?
A: Absolutely! Calculators are highly efficient for percentage calculations, especially for more complex problems. However, understanding the underlying principles remains crucial.
Q: What if the percentage calculation results in a decimal?
A: Depending on the context, you might round the decimal to the nearest whole number or keep it as a decimal. For example, in financial calculations, precision is vital, while rounding might suffice for general estimations.
Q: Are there online tools or software for percentage calculations?
A: Yes, many online calculators and spreadsheet software (like Excel or Google Sheets) offer built-in functions for various percentage calculations.
Q: How can I improve my skills in percentage calculations?
A: Practice is key! Work through various examples and problems, starting with simpler ones and gradually moving towards more complex calculations. Understanding the underlying principles is essential for mastering percentage calculations.
Conclusion
Understanding "What is 25% of 90?" is more than just a simple calculation; it's a gateway to comprehending the fundamental concepts of percentages and their far-reaching applications. Percentages are a ubiquitous tool in various fields, and mastering their calculation and interpretation enhances problem-solving skills and empowers you to navigate numerous aspects of daily life, finance, and other disciplines. By employing different calculation methods and understanding their context, you'll be well-equipped to handle a wide range of percentage-based problems confidently and efficiently. Remember to practice and explore diverse applications to solidify your understanding and apply this valuable mathematical concept to real-world scenarios.
Latest Posts
Latest Posts
-
Parts Of A Circle Labelled
Sep 20, 2025
-
Logic Circuit With Truth Table
Sep 20, 2025
-
Good Luck Wishes For Interview
Sep 20, 2025
-
Is 147 A Prime Number
Sep 20, 2025
-
Venture Capital Vs Private Equity
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.