What Is 3 X 4
elan
Sep 22, 2025 · 6 min read
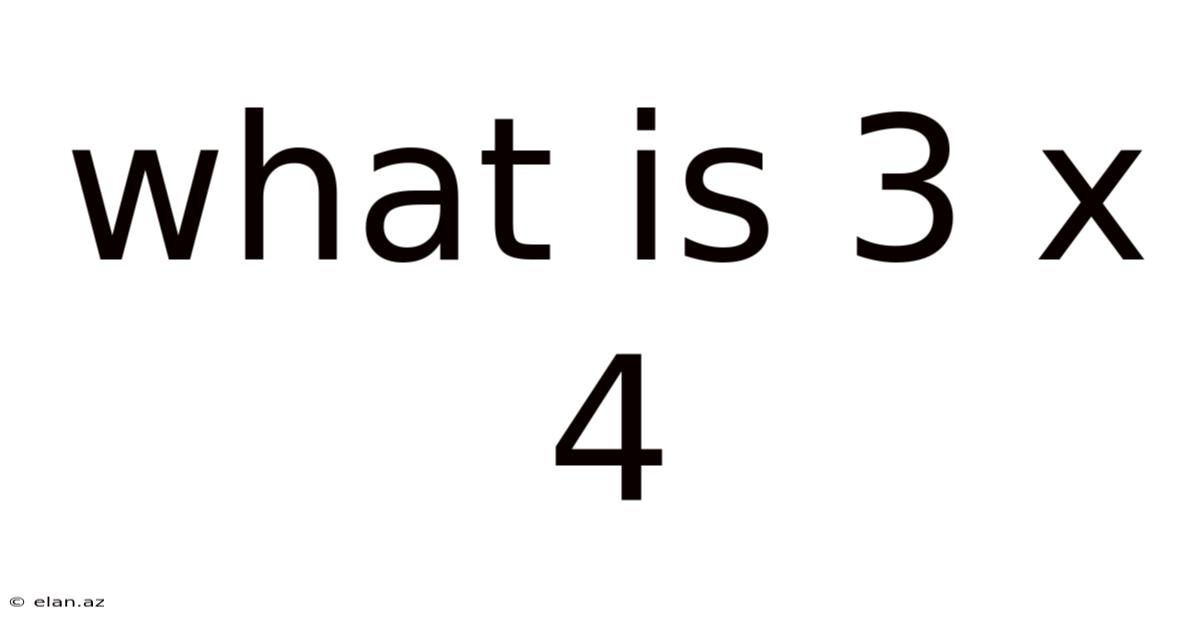
Table of Contents
What is 3 x 4? Unpacking Multiplication and its Real-World Applications
This seemingly simple question, "What is 3 x 4?", opens the door to a fascinating exploration of mathematics, specifically multiplication. While the answer itself is straightforward (12), the underlying concepts and applications extend far beyond a simple calculation. This article delves into the meaning of multiplication, explores different ways to understand 3 x 4, examines its applications in various fields, and addresses frequently asked questions. Understanding multiplication is fundamental to numeracy and forms the bedrock for more advanced mathematical concepts.
Understanding Multiplication: Beyond Rote Memorization
Multiplication, at its core, is repeated addition. When we say 3 x 4, we are essentially saying "add 3 four times" or "add 4 three times." This understanding is crucial, especially for young learners who are first grappling with the concept. Instead of memorizing multiplication tables as isolated facts, understanding the underlying principle of repeated addition provides a solid foundation for mathematical reasoning.
Let's visualize 3 x 4:
- Repeated Addition: 3 + 3 + 3 + 3 = 12 or 4 + 4 + 4 = 12
This simple visual representation connects the abstract concept of multiplication to a concrete reality. This method helps to build an intuitive grasp of multiplication, reducing reliance on rote memorization alone.
Visualizing 3 x 4: Arrays and Area Models
Beyond repeated addition, we can visualize 3 x 4 using arrays and area models. These visual tools provide a different perspective, reinforcing the concept of multiplication in a concrete and engaging way.
-
Arrays: Imagine arranging 3 rows of 4 objects each. This forms a rectangular array. Counting the total number of objects gives us the answer: 12. This method is particularly helpful in visualizing the commutative property of multiplication (3 x 4 = 4 x 3).
-
Area Models: Imagine a rectangle with a length of 4 units and a width of 3 units. The area of this rectangle represents the product of 3 x 4. By dividing the rectangle into smaller squares (each representing a unit of area), we can visually count 12 squares, thereby illustrating the result of 3 x 4.
These visual methods are not just for elementary school children. They provide a powerful way to understand the relationship between multiplication and geometric concepts, fostering a deeper understanding of the subject.
The Commutative Property: 3 x 4 = 4 x 3
A key property of multiplication is the commutative property. This property states that changing the order of the numbers being multiplied does not change the result. In other words, 3 x 4 is equal to 4 x 3. This may seem obvious, but understanding this property is crucial for solving more complex equations and for simplifying calculations.
Visualizing this using arrays makes it clear. If you have 3 rows of 4 objects, you can just as easily rotate the array to have 4 rows of 3 objects, and the total number of objects remains the same – 12.
Beyond the Basics: Applications of Multiplication
The seemingly simple equation "3 x 4 = 12" has far-reaching applications in numerous fields. Let's explore some examples:
-
Everyday Life: Calculating the total cost of multiple items (e.g., 3 items at $4 each), determining the total number of objects (e.g., 3 bags with 4 apples each), or calculating distances (e.g., traveling 3 kilometers four times).
-
Cooking and Baking: Scaling recipes (e.g., multiplying ingredient quantities to make a larger batch), calculating serving sizes, or determining the number of items needed (e.g., 3 batches of cookies, each using 4 eggs).
-
Business and Finance: Calculating total revenue (e.g., selling 3 products at $4 each), calculating profits, or determining interest earned.
-
Science and Engineering: In physics, multiplication is used extensively in calculating forces, velocities, and accelerations. In chemistry, it's used in stoichiometry to calculate the amounts of reactants and products in chemical reactions.
-
Computer Science: Multiplication is a fundamental operation in computer programming, used in various algorithms and calculations. It forms the basis for more complex mathematical operations within software and hardware.
-
Construction and Design: Calculating the amount of materials needed for a project (e.g., 3 walls needing 4 liters of paint each), determining dimensions, or calculating the volume or area of structures.
The Significance of Multiplication in Advanced Mathematics
Multiplication forms the basis for many advanced mathematical concepts. It is essential for understanding:
-
Exponents: Raising a number to a power (e.g., 3⁴) involves repeated multiplication.
-
Algebra: Solving algebraic equations often requires applying multiplication and its inverse operation, division.
-
Calculus: Multiplication is essential in calculating derivatives and integrals, fundamental concepts in calculus.
-
Geometry: Calculating areas and volumes relies heavily on multiplication.
-
Statistics and Probability: Multiplication plays a significant role in calculating probabilities and statistical measures.
Frequently Asked Questions (FAQs)
Q: Why is multiplication important?
A: Multiplication is a fundamental mathematical operation that simplifies repeated addition, making complex calculations more efficient. It's essential for problem-solving in various fields and forms the basis for more advanced mathematical concepts.
Q: How can I help my child learn multiplication?
A: Use visual aids like arrays and area models. Start with repeated addition, then gradually introduce multiplication tables. Make it fun with games and real-world examples.
Q: Is there a faster way to calculate 3 x 4 besides repeated addition?
A: Most people memorize multiplication facts, making the calculation almost instantaneous. However, understanding the concept of repeated addition provides a fallback method for quickly verifying the answer.
Q: What happens when you multiply by zero?
A: Any number multiplied by zero is always zero (e.g., 3 x 0 = 0). This is because multiplication represents repeated addition, and adding zero repeatedly results in zero.
Q: What happens when you multiply by one?
A: Any number multiplied by one is always itself (e.g., 3 x 1 = 3). This is because multiplication represents repeated addition, and adding a number once results in that same number.
Conclusion: The Power of Understanding 3 x 4
While the answer to "What is 3 x 4?" is simply 12, the journey to understanding this seemingly basic equation unveils a profound insight into the world of mathematics. From the fundamental principle of repeated addition to its widespread applications in various fields and its role as a building block for advanced mathematical concepts, multiplication is a cornerstone of numeracy. By embracing visual representations, exploring real-world applications, and understanding its underlying principles, we unlock not just the answer to a simple multiplication problem, but a deeper appreciation for the power and beauty of mathematics. The ability to understand and apply multiplication is not just a mathematical skill; it's a tool that empowers us to solve problems, understand the world around us, and succeed in countless endeavors.
Latest Posts
Latest Posts
-
7 Features Of Living Things
Sep 22, 2025
-
How To Calculate Closing Inventory
Sep 22, 2025
-
Shortest Distance Between Two Lines
Sep 22, 2025
-
Fixed Assets Or Current Assets
Sep 22, 2025
-
Words That Rhyme With Boat
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.