What Is 60 Of 90
elan
Sep 16, 2025 · 5 min read
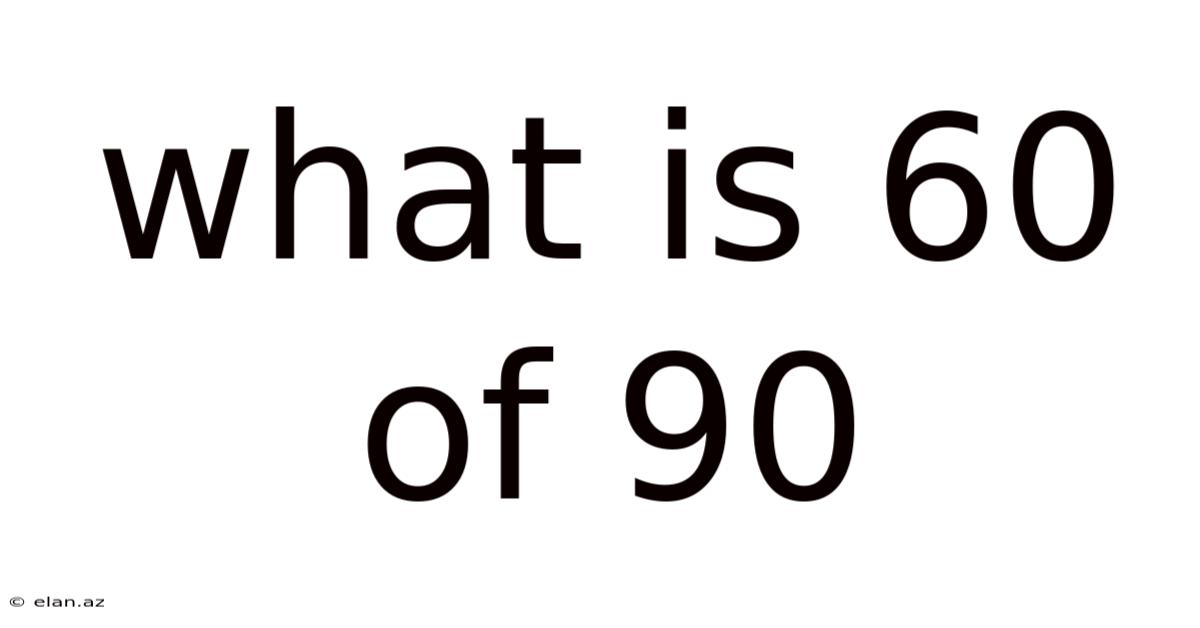
Table of Contents
What is 60 of 90? Unpacking Percentages, Fractions, and Ratios
Finding "60 of 90" might seem like a simple arithmetic problem, but it opens a door to understanding fundamental mathematical concepts like percentages, fractions, and ratios. This seemingly straightforward query allows us to explore these concepts in depth, showcasing their interconnectedness and practical applications in everyday life. This article will delve into the various ways to interpret and solve "60 of 90," providing a comprehensive explanation suitable for learners of all levels.
Understanding the Question: Different Interpretations
The phrase "60 of 90" can be interpreted in several ways, depending on the context. Let's examine the most common interpretations:
-
60 out of 90: This is the most straightforward interpretation. It implies a part-to-whole relationship, where 60 represents a portion of a total of 90. This is directly related to the concept of fractions and percentages.
-
60 as a proportion of 90: This focuses on the relative size of 60 compared to 90. We're interested in determining the ratio between these two numbers.
-
60 multiplied by a fraction of 90: This interpretation can arise in scenarios where 60 represents a quantity that is being scaled or reduced proportionally based on the relationship with 90.
Method 1: Calculating the Fraction
The most intuitive approach to solving "60 of 90" is to express it as a fraction. The fraction represents the part (60) over the whole (90):
60/90
This fraction can be simplified by finding the greatest common divisor (GCD) of 60 and 90, which is 30. Dividing both the numerator and the denominator by 30, we get:
60 ÷ 30 / 90 ÷ 30 = 2/3
Therefore, 60 out of 90 is equivalent to 2/3. This fraction represents the proportionate relationship between 60 and 90. It indicates that 60 constitutes two-thirds of 90.
Method 2: Calculating the Percentage
To express "60 of 90" as a percentage, we need to determine what proportion of 90 is represented by 60. We can do this using the following formula:
(Part / Whole) * 100%
Substituting our values:
(60 / 90) * 100% = 0.666... * 100% ≈ 66.67%
Therefore, 60 is approximately 66.67% of 90. The recurring decimal indicates that this percentage is not exact, but a close approximation.
Method 3: Understanding Ratios
The relationship between 60 and 90 can also be expressed as a ratio. A ratio shows the relative size of two or more values. The ratio of 60 to 90 is written as:
60:90
Similar to fractions, this ratio can be simplified by dividing both sides by their GCD (30):
60 ÷ 30 : 90 ÷ 30 = 2:3
This simplified ratio, 2:3, conveys the same information as the fraction 2/3 – that 60 is two-thirds of 90.
Applying these Concepts: Real-World Examples
These mathematical concepts – fractions, percentages, and ratios – are crucial for various real-world applications. Let's consider a few examples:
-
Academic Performance: If a student answers 60 out of 90 questions correctly on a test, their score is 66.67%. This allows for easy comparison with other students and provides a clear indication of their understanding of the subject matter.
-
Business and Finance: In a business context, if 60 out of 90 products sold are of a particular type, this indicates a market share of 66.67% for that product. This information is vital for business decision-making and strategy.
-
Data Analysis: In statistical analysis, representing data as fractions, percentages, or ratios helps to simplify complex information and make it easier to understand trends and patterns. For example, in a survey of 90 people, 60 responded positively, representing 66.67% positive response rate.
-
Recipe Scaling: If a recipe calls for 90 grams of flour and you only want to make two-thirds of the recipe, you would use 60 grams of flour (2/3 * 90g = 60g).
-
Project Completion: If a project consists of 90 tasks and 60 are already completed, the project's completion rate stands at 66.67%.
Expanding the Understanding: Further Mathematical Exploration
The concept of "60 of 90" opens the door to exploring more complex mathematical concepts:
-
Proportions: Solving problems involving proportions relies heavily on understanding fractions and ratios. A proportion is a statement that two ratios are equal. For example, we can set up a proportion to solve problems like: "If 60 out of 90 apples are red, how many red apples would you expect in a batch of 150 apples?"
-
Probability: The fraction 2/3 can also be interpreted as a probability. If you randomly select an item from a set of 90 items, where 60 are of a specific type, the probability of selecting an item of that type is 2/3.
-
Algebra: We can represent "60 of 90" algebraically. Let 'x' represent the percentage. We can set up the equation: (60/90) * 100 = x. Solving for x gives us the percentage value.
-
Advanced Statistical Analysis: In more advanced statistical analysis, understanding proportions and ratios is crucial for interpreting various statistical measures like relative risk and odds ratios.
Frequently Asked Questions (FAQ)
-
What is the simplest form of the fraction 60/90? The simplest form is 2/3.
-
How do I convert a fraction to a percentage? Multiply the fraction by 100%.
-
What is the ratio of 60 to 90 in its simplest form? The simplest form is 2:3.
-
Can I use a calculator to solve this? Yes, you can use a calculator to perform the division (60/90) and then multiply by 100% to find the percentage.
-
Are there other ways to express the relationship between 60 and 90? Yes, you can also use decimal representation (0.666...).
Conclusion: Beyond the Numbers
The seemingly simple question "What is 60 of 90?" has allowed us to explore fundamental mathematical concepts – fractions, percentages, and ratios – and their applications in various real-world scenarios. Understanding these concepts is not just about memorizing formulas; it's about developing a deeper understanding of quantitative relationships and their practical significance. By mastering these basic principles, we equip ourselves with valuable tools for tackling more complex mathematical problems and interpreting data effectively in our daily lives. The journey from a simple arithmetic question to a deeper exploration of mathematical concepts highlights the beauty and utility of mathematics in understanding our world.
Latest Posts
Latest Posts
-
5 Letter Word Ending St
Sep 16, 2025
-
Requisition Letter For Salary Increment
Sep 16, 2025
-
Yours Faithfully Or Yours Sincerely
Sep 16, 2025
-
Convert Imperial To Metric Chart
Sep 16, 2025
-
Tongue Tie Vs Normal Adults
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.