Whats 20 Percent Of 70
elan
Sep 21, 2025 · 5 min read
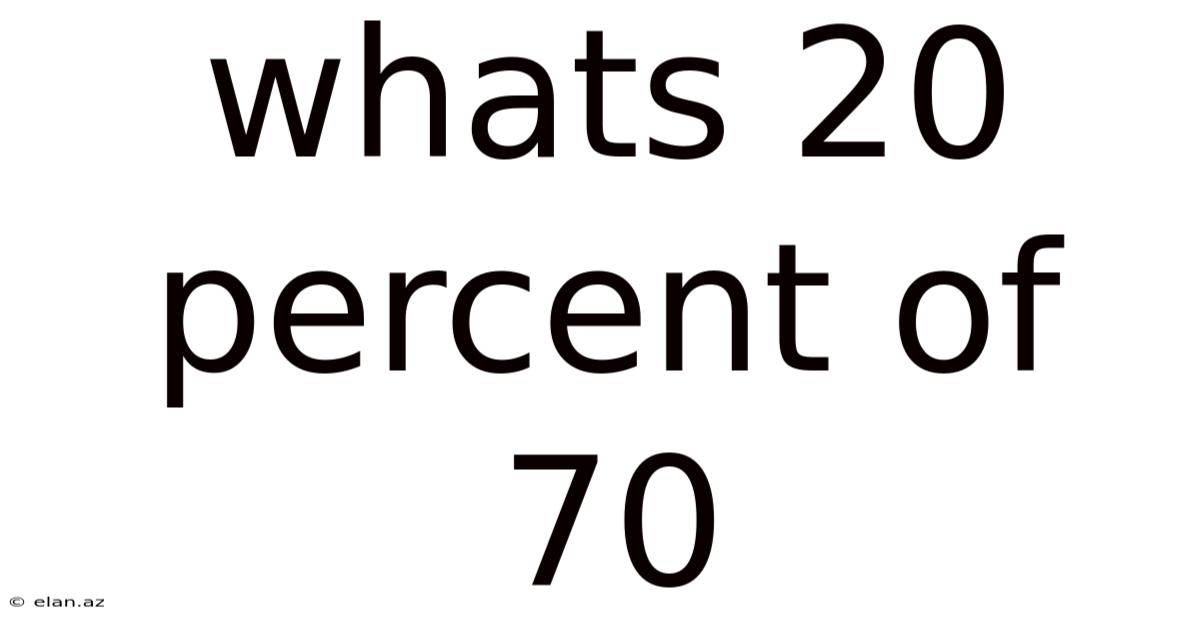
Table of Contents
What's 20 Percent of 70? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 70 might seem like a simple task, readily solvable with a quick calculation. But this seemingly straightforward question opens a door to a much broader understanding of percentages, their practical applications in everyday life, and even their role in more complex mathematical concepts. This article will not only answer the initial question but will also explore the underlying principles, various methods of calculation, and real-world examples to solidify your understanding of percentages.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 20 percent means 20 out of 100, or 20/100, which simplifies to 1/5. This foundational understanding is crucial for tackling any percentage problem. Understanding this fraction equivalence is key to solving problems involving percentages.
Method 1: The Direct Calculation Method
The most straightforward way to calculate 20 percent of 70 is to convert the percentage into a decimal and then multiply. Remember, to convert a percentage to a decimal, you divide by 100.
-
Step 1: Convert the percentage to a decimal: 20% / 100 = 0.20
-
Step 2: Multiply the decimal by the number: 0.20 * 70 = 14
Therefore, 20 percent of 70 is $\boxed{14}$.
Method 2: The Fraction Method
As mentioned earlier, 20% is equivalent to the fraction 1/5. This allows us to solve the problem using fractions:
-
Step 1: Express the percentage as a fraction: 20% = 1/5
-
Step 2: Multiply the fraction by the number: (1/5) * 70 = 70/5
-
Step 3: Simplify the fraction: 70/5 = 14
Again, we arrive at the answer: 20 percent of 70 is $\boxed{14}$.
Method 3: Using Proportions
The concept of percentages can also be understood through proportions. We can set up a proportion to solve the problem:
-
Step 1: Set up the proportion: 20/100 = x/70 (where 'x' represents the unknown value, 20% of 70)
-
Step 2: Cross-multiply: 20 * 70 = 100 * x
-
Step 3: Solve for x: 1400 = 100x => x = 1400/100 = 14
This method reinforces the relationship between percentages and ratios, further solidifying the understanding of the concept.
Real-World Applications of Percentages
Percentages are ubiquitous in our daily lives. They are used extensively in various fields, making understanding them crucial for informed decision-making. Here are a few examples:
-
Sales and Discounts: Stores often advertise discounts as percentages. Understanding percentages helps consumers calculate the actual price after a discount. For example, a 20% discount on a $70 item is $14, resulting in a final price of $56.
-
Taxes: Sales tax and income tax are calculated as percentages. Knowing how to calculate percentages is vital for budgeting and managing finances effectively.
-
Tips and Gratuities: Calculating tips in restaurants often involves determining a percentage of the total bill. A 20% tip on a $70 meal would be $14.
-
Interest Rates: Interest on loans, savings accounts, and investments is typically expressed as a percentage. Understanding percentage calculations is essential for making informed financial decisions.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting statistical data. Graphs, charts, and reports often utilize percentages to represent proportions and trends.
Beyond the Basics: More Complex Percentage Calculations
While finding 20% of 70 is relatively simple, percentages can be involved in more complex calculations. For instance:
-
Finding the original value: If you know the percentage and the resulting value after a percentage increase or decrease, you can work backward to find the original value. For example, if an item costs $56 after a 20% discount, you can calculate the original price using algebraic equations.
-
Calculating percentage increase or decrease: Understanding the difference between a percentage increase and a percentage decrease is important. These calculations require an understanding of how to apply the percentage change to the base value.
-
Compound interest: Compound interest involves calculating interest on both the principal amount and accumulated interest. This concept often requires repeated percentage calculations over time.
Frequently Asked Questions (FAQ)
Q: How do I calculate a percentage of a number without a calculator?
A: You can use the methods described above – direct calculation using decimals, the fraction method, or proportions – to calculate percentages without a calculator. However, the fraction method is often the easiest for mental calculation, especially with common percentages like 20%, 25%, 50%, and so on.
Q: What if the percentage isn't a whole number (e.g., 17.5%)?
A: The same methods apply. Simply convert the percentage to a decimal (17.5% = 0.175) and multiply by the number.
Q: Are there any shortcuts for calculating common percentages?
A: Yes. For instance, 10% of a number is simply the number divided by 10. 5% is half of 10%, and so on. Learning these shortcuts can make percentage calculations much faster.
Q: How can I improve my understanding of percentages?
A: Practice is key. Solve various percentage problems, using different methods, to build your confidence and understanding. Try working through examples from different contexts, such as discounts, taxes, and interest rates.
Conclusion
Finding 20 percent of 70, while seemingly a basic arithmetic problem, serves as an excellent entry point for understanding the broader concept of percentages. Mastering percentage calculations is crucial for navigating various aspects of daily life, from personal finance to professional fields. By understanding the fundamental principles and applying the different calculation methods, you can confidently tackle any percentage problem and appreciate its widespread applications. Remember that consistent practice and exploring different scenarios are key to building a strong foundation in this essential mathematical skill. The more you work with percentages, the more intuitive and effortless they will become.
Latest Posts
Latest Posts
-
Examples Of Non Reducing Sugars
Sep 21, 2025
-
How To Draw A Earth
Sep 21, 2025
-
Ionisation Energy A Level Chemistry
Sep 21, 2025
-
Words That Start With Ru
Sep 21, 2025
-
Expression Of Admiration 6 Letters
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.