Whats 3/5 As A Percent
elan
Sep 10, 2025 · 6 min read
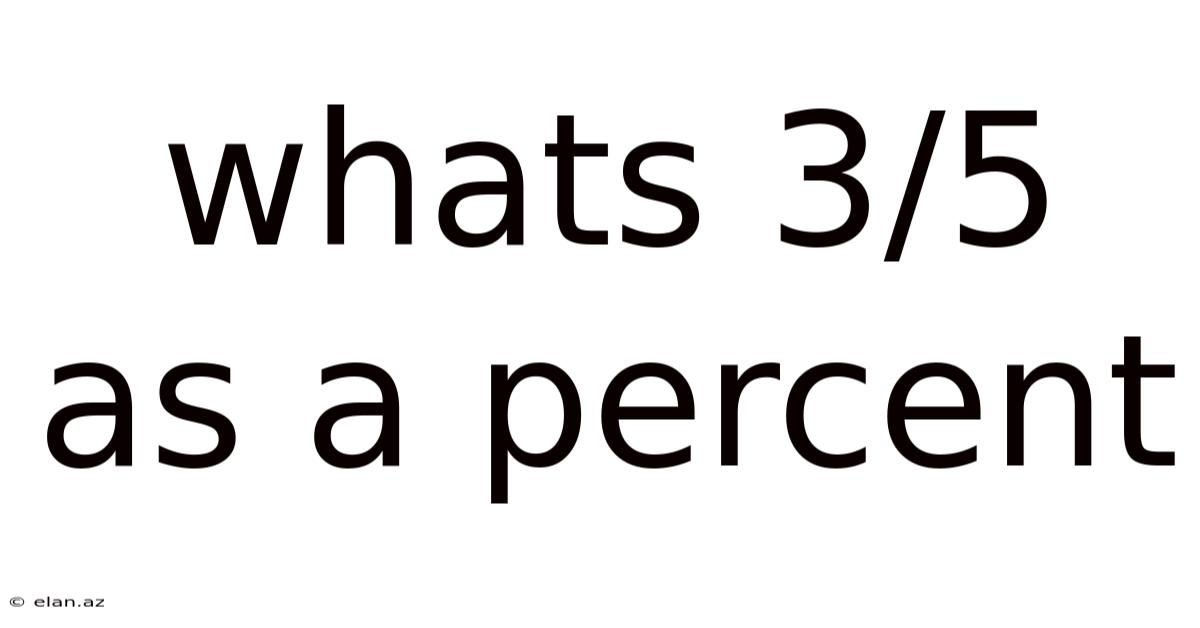
Table of Contents
What's 3/5 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversions
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from finance and cooking to data analysis and everyday life. This comprehensive guide will delve into the process of converting 3/5 to a percentage, explaining the underlying principles and providing you with the tools to tackle similar conversions with ease. We'll explore multiple methods, ensuring a complete understanding regardless of your mathematical background. This guide will also cover common mistakes and provide you with a strong foundation for future fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before we dive into the conversion of 3/5, let's briefly refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/5, 3 is the numerator and 5 is the denominator. This means we have 3 parts out of a total of 5 equal parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of a hundred. For instance, 25% means 25 out of 100, which is equivalent to the fraction 25/100, or simplified, 1/4.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is arguably the most straightforward method. We first convert the fraction 3/5 into a decimal and then multiply by 100 to express it as a percentage.
-
Convert the fraction to a decimal: To do this, we divide the numerator (3) by the denominator (5):
3 ÷ 5 = 0.6
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%):
0.6 × 100 = 60%
Therefore, 3/5 is equal to 60%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction of 3/5 that has a denominator of 100. Since percentages are based on 100, this directly gives us the percentage.
-
Determine the scaling factor: To change the denominator from 5 to 100, we need to multiply by 20 (100 ÷ 5 = 20).
-
Apply the scaling factor to both the numerator and the denominator: We must multiply both the numerator and the denominator by the same factor to maintain the value of the fraction.
(3 × 20) / (5 × 20) = 60/100
-
Express as a percentage: Since the denominator is now 100, the numerator directly represents the percentage.
60/100 = 60%
Thus, using this method, we again find that 3/5 is equal to 60%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the unknown percentage. We can set up a proportion where one ratio represents the fraction and the other represents the percentage over 100.
-
Set up the proportion:
3/5 = x/100
Here, 'x' represents the unknown percentage we're trying to find.
-
Cross-multiply: To solve for 'x', we cross-multiply:
5x = 300
-
Solve for x: Divide both sides of the equation by 5:
x = 60
Therefore, x = 60%, confirming that 3/5 is equivalent to 60%.
The Importance of Understanding the Underlying Principles
While these methods offer different approaches to the same problem, understanding the underlying principles is crucial for solving more complex fraction-to-percentage conversions. The core concept is the relationship between fractions, decimals, and percentages – they are all different ways of representing the same proportion. Mastering this relationship allows you to confidently tackle any fraction-to-percentage conversion.
Expanding the Concept: Working with More Complex Fractions
Let's now apply these principles to a slightly more complex example. Suppose we want to convert 7/8 to a percentage.
Method 1: Decimal to Percentage
- Convert the fraction to a decimal: 7 ÷ 8 = 0.875
- Convert the decimal to a percentage: 0.875 × 100 = 87.5%
Method 2: Equivalent Fraction
- Determine the scaling factor: There isn't a whole number that easily converts 8 to 100. We can use decimals. 100/8 = 12.5
- Apply the scaling factor: (7 × 12.5) / (8 × 12.5) = 87.5/100 = 87.5%
Method 3: Proportions
- Set up the proportion: 7/8 = x/100
- Cross-multiply: 8x = 700
- Solve for x: x = 87.5%
As you can see, the same principles apply regardless of the complexity of the fraction.
Common Mistakes to Avoid
- Incorrectly multiplying by 10: Remember, to convert a decimal to a percentage, you must multiply by 100, not 10.
- Forgetting the percentage sign (%): Always include the percentage symbol to indicate that your answer is a percentage.
- Mixing up the numerator and denominator: Ensure you are dividing the numerator by the denominator when converting a fraction to a decimal.
- Rounding errors: Be mindful of rounding errors, especially when dealing with decimals. Try to maintain accuracy throughout the calculation.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, absolutely! Most calculators have the functionality to perform these conversions directly. However, understanding the underlying methods is essential for building a strong mathematical foundation and handling situations where a calculator isn't readily available.
Q: What if the fraction is an improper fraction (numerator > denominator)?
A: An improper fraction will result in a percentage greater than 100%. For example, 5/2 (2.5 as a decimal) would be 250%. This simply means you have more than the whole.
Q: What if I have a mixed number (a whole number and a fraction)?
A: Convert the mixed number into an improper fraction first, and then apply any of the methods discussed above. For example, 1 1/2 would first become 3/2, and then you can proceed with the conversion.
Q: Are there other ways to convert fractions to percentages?
A: While the methods discussed here are the most common and straightforward, other advanced techniques exist, particularly in algebra and calculus. However, for basic fraction-to-percentage conversions, these methods are sufficient.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with wide-ranging applications. This guide has provided you with three different methods to tackle these conversions, empowering you to choose the approach that best suits your understanding and the specific problem. Remember to practice regularly, focusing on understanding the underlying principles to build confidence and mastery in this essential skill. By understanding the interconnectedness of fractions, decimals, and percentages, you will unlock a deeper understanding of numerical representation and proportion, opening doors to more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Difference Between Horse And Donkey
Sep 10, 2025
-
Community Of Flora And Fauna
Sep 10, 2025
-
1 Third As A Percentage
Sep 10, 2025
-
Ionic Covalent And Metallic Bonds
Sep 10, 2025
-
Square Root Of 4761 Joke
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Whats 3/5 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.