X 2 2x 1 0
elan
Sep 20, 2025 · 6 min read
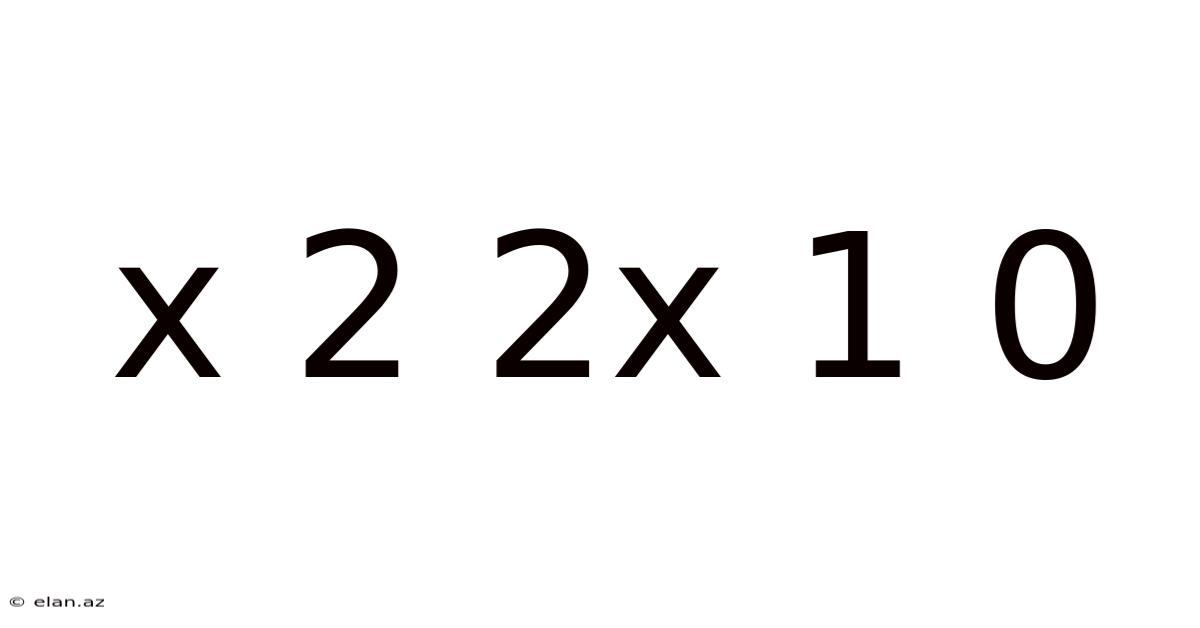
Table of Contents
Decoding the Mystery: A Deep Dive into x² + 2x + 1 = 0
The equation x² + 2x + 1 = 0 might seem deceptively simple at first glance. It's a quadratic equation, a fundamental concept in algebra that forms the bedrock for many more complex mathematical concepts. Understanding how to solve this equation, and more importantly, why the methods work, unlocks a world of possibilities in mathematics and its applications. This article will guide you through various methods of solving this specific equation, explore its underlying mathematical principles, and delve into related concepts to provide a comprehensive understanding.
Introduction: What is a Quadratic Equation?
Before we tackle x² + 2x + 1 = 0, let's establish a foundation. A quadratic equation is any equation that can be written in the standard form: ax² + bx + c = 0, where 'a', 'b', and 'c' are constants (numbers), and 'a' is not equal to zero (if a=0, it becomes a linear equation). Our equation, x² + 2x + 1 = 0, fits this form perfectly, with a = 1, b = 2, and c = 1. Understanding quadratic equations is crucial for solving problems in various fields, including physics, engineering, and economics.
Method 1: Factoring
This is often the quickest and easiest method for solving simple quadratic equations. Factoring involves rewriting the equation as a product of two simpler expressions. Observe our equation: x² + 2x + 1 = 0. This is a perfect square trinomial. Notice that:
- x² is the square of x (x * x)
- 1 is the square of 1 (1 * 1)
- 2x is twice the product of x and 1 (2 * x * 1)
Therefore, we can factor the equation as:
(x + 1)(x + 1) = 0 or (x + 1)² = 0
This means that the expression (x + 1) must be equal to zero. Solving for x:
x + 1 = 0 x = -1
Therefore, the solution to the equation x² + 2x + 1 = 0 is x = -1. This is a repeated root, meaning the equation has only one solution, which occurs twice.
Method 2: Quadratic Formula
The quadratic formula is a powerful tool that can solve any quadratic equation, regardless of whether it's easily factorable. The formula is derived from completing the square (a method we'll explore later) and is expressed as:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 2, c = 1):
x = [-2 ± √(2² - 4 * 1 * 1)] / (2 * 1) x = [-2 ± √(4 - 4)] / 2 x = [-2 ± √0] / 2 x = -2 / 2 x = -1
Again, we arrive at the solution x = -1. The quadratic formula confirms our previous result, demonstrating its versatility.
Method 3: Completing the Square
This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's apply it to x² + 2x + 1 = 0:
- Move the constant term to the right side:
x² + 2x = -1
- Take half of the coefficient of x (which is 2), square it (1² = 1), and add it to both sides:
x² + 2x + 1 = -1 + 1
- Factor the left side as a perfect square:
(x + 1)² = 0
- Solve for x:
x + 1 = 0 x = -1
Completing the square provides a systematic approach to solving quadratic equations, especially useful when dealing with equations that are not easily factorable.
Graphical Representation: Understanding the Parabola
Quadratic equations represent parabolas when graphed on a coordinate plane. The equation x² + 2x + 1 = 0 represents a parabola that opens upwards. The solution to the equation (x = -1) represents the x-intercept – the point where the parabola intersects the x-axis. In this case, the parabola is tangent to the x-axis at x = -1, indicating a repeated root. The vertex of the parabola, which represents the minimum value of the quadratic function, is located at (-1, 0).
The Discriminant: Unveiling the Nature of Roots
The expression inside the square root in the quadratic formula, b² - 4ac, is called the discriminant. It provides valuable information about the nature of the roots of a quadratic equation:
-
If the discriminant is positive (b² - 4ac > 0): The equation has two distinct real roots. The parabola intersects the x-axis at two different points.
-
If the discriminant is zero (b² - 4ac = 0): The equation has one repeated real root (or a double root). The parabola touches the x-axis at only one point. This is the case with our equation x² + 2x + 1 = 0.
-
If the discriminant is negative (b² - 4ac < 0): The equation has two complex roots (involving imaginary numbers). The parabola does not intersect the x-axis.
Applications of Quadratic Equations:
Quadratic equations are not just abstract mathematical concepts; they have wide-ranging applications in various fields:
-
Physics: Projectile motion, calculating the trajectory of a ball or rocket, often involves solving quadratic equations.
-
Engineering: Designing bridges, buildings, and other structures frequently requires using quadratic equations to determine optimal dimensions and structural integrity.
-
Economics: Modeling economic growth, analyzing cost functions, and predicting market trends often involve quadratic equations.
-
Computer Graphics: Creating curved shapes and animations in computer graphics heavily relies on quadratic functions and their properties.
Further Exploration: Beyond the Basics
While we focused on x² + 2x + 1 = 0, the principles and methods discussed extend to all quadratic equations. Exploring more complex quadratic equations, dealing with irrational or complex roots, and understanding the connection between quadratic equations and conic sections (circles, ellipses, parabolas, hyperbolas) will deepen your understanding of this fundamental mathematical concept. Consider exploring topics like completing the square with more complex equations, solving systems of quadratic equations, or delving into the world of polynomial equations of higher degrees.
Frequently Asked Questions (FAQs):
-
Q: What does it mean when a quadratic equation has a repeated root?
- A: A repeated root means the quadratic equation has only one solution, which appears twice. Graphically, this means the parabola touches the x-axis at only one point.
-
Q: Can all quadratic equations be solved by factoring?
- A: No, not all quadratic equations can be easily factored. The quadratic formula or completing the square are more general methods that can solve any quadratic equation.
-
Q: What is the significance of the discriminant?
- A: The discriminant tells us the nature of the roots of a quadratic equation – whether they are real or complex, and whether they are distinct or repeated.
-
Q: How can I improve my skills in solving quadratic equations?
- A: Practice is key! Solve a variety of quadratic equations using different methods. Start with simpler examples and gradually progress to more challenging ones. Understanding the underlying concepts is crucial for mastering the techniques.
Conclusion: Mastering the Fundamentals
The seemingly simple equation x² + 2x + 1 = 0 serves as a gateway to a vast and fascinating world of mathematics. By understanding the different methods for solving this equation and grasping the underlying concepts like factoring, the quadratic formula, completing the square, and the discriminant, you build a strong foundation for tackling more complex mathematical challenges. Remember, the journey of mathematical learning is a continuous process of exploration and discovery. Embrace the challenges, and you'll find that the rewards are immense.
Latest Posts
Latest Posts
-
1 79 M Height In Feet
Sep 20, 2025
-
Simple Annual Leave Request Letter
Sep 20, 2025
-
How To Calculate Hdi Index
Sep 20, 2025
-
A Level Maths Integration Questions
Sep 20, 2025
-
Why Do Metals Conduct Electricity
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 1 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.