X 3 X 2 2x
elan
Sep 24, 2025 · 6 min read
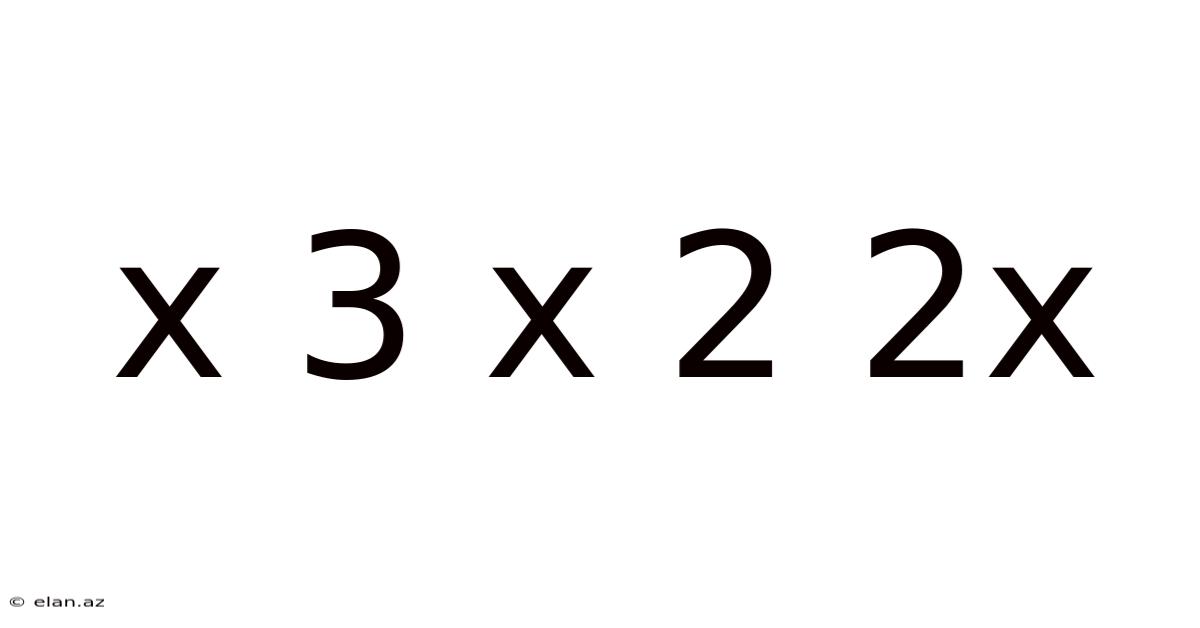
Table of Contents
Decoding the Mathematical Expression: x³ x² 2x
This article delves into the mathematical expression x³ x² 2x, exploring its simplification, applications, and underlying principles. We will unravel the mysteries behind this seemingly simple expression, revealing its power and versatility in various mathematical contexts. Understanding this expression provides a foundation for more complex algebraic manipulations and problem-solving. We’ll cover simplification techniques, explore its graphical representation, and address frequently asked questions.
Understanding the Components
Before we dive into simplifying the expression, let's break down its individual components:
-
x³ (x cubed): This represents x multiplied by itself three times (x * x * x). It's a term with a variable (x) raised to the power of 3. The power indicates the number of times the base (x) is multiplied by itself.
-
x² (x squared): This represents x multiplied by itself twice (x * x). It's another term with the variable x raised to the power of 2.
-
2x: This represents 2 multiplied by x. It's a term with a coefficient (2) and a variable (x). The coefficient is a numerical factor that multiplies the variable.
Simplifying the Expression
The expression x³ x² 2x involves terms with the same variable (x). This allows us to simplify the expression using the rules of exponents and algebraic addition. The key rule to remember is that when multiplying terms with the same base, we add their exponents.
-
Combining like terms: The expression can be rewritten as: x³ * x² * 2x
-
Applying the exponent rule: When multiplying terms with the same base (x), we add the exponents: 3 + 2 + 1 = 6. Remember that 2x is equivalent to 2x¹, so the exponent of the last term is 1.
-
Simplified expression: Therefore, x³ x² 2x simplifies to 2x⁶.
Graphical Representation
The simplified expression, 2x⁶, represents a polynomial function. Graphically, this function depicts a curve. The shape and behavior of this curve depend on the value of 'x'.
-
Even Power: The even power (6) indicates that the graph will be symmetrical about the y-axis. This means that if you reflect the graph across the y-axis, it will overlap itself.
-
Positive Coefficient: The positive coefficient (2) means that the graph will extend upwards as x increases (positive infinity) and upwards as x decreases (negative infinity).
-
Degree of the Polynomial: The degree of the polynomial (6) signifies that the graph will have at most 5 turning points (points where the curve changes direction). These turning points aren't easily determinable without using calculus, but understanding the degree gives us a general idea of the graph's complexity.
Visualizing this graph requires plotting points for different x-values. For example:
- If x = 0, 2x⁶ = 0
- If x = 1, 2x⁶ = 2
- If x = 2, 2x⁶ = 128
- If x = -1, 2x⁶ = 2
- If x = -2, 2x⁶ = 128
Plotting these points and connecting them smoothly will give you a visual representation of the 2x⁶ function. The graph will start from the origin (0,0) and rise steeply as x moves away from zero in either the positive or negative direction.
Applications in Various Fields
The simplified expression 2x⁶, and its underlying principles, have far-reaching applications across numerous fields:
-
Physics: Polynomial functions like 2x⁶ are used to model various physical phenomena, such as the trajectory of projectiles, the displacement of an object under certain forces, or the relationship between variables in complex systems.
-
Engineering: Engineers utilize such expressions in structural analysis, designing systems, and modeling the behavior of materials under stress.
-
Economics: Polynomial functions can be used to model economic growth, production functions, and consumer demand. Understanding these relationships is crucial for economic forecasting and policymaking.
-
Computer Science: Polynomial functions form the basis of numerous algorithms and are used in computational modeling and simulations. They are fundamental to fields like computer graphics and machine learning.
-
Statistics: Polynomial regression, a statistical technique that uses polynomial functions to model the relationship between variables, is widely used in data analysis and forecasting.
Further Exploration: Expanding the Expression
Let's consider a slightly more complex scenario. Suppose we have the expression: (x + 1)³ (x + 2)² 2(x + 3)
This expression involves expanding the binomials before simplification. We would use the binomial theorem or Pascal's triangle for expanding the cubed and squared terms. For example:
(x + 1)³ = x³ + 3x² + 3x + 1 (Using the binomial theorem or Pascal's Triangle)
(x + 2)² = x² + 4x + 4
Once these terms are expanded, we would then multiply them together and collect like terms, eventually leading to a simplified polynomial expression of a higher degree. This process involves a more extensive application of algebraic manipulation.
Frequently Asked Questions (FAQ)
Q1: Can the expression x³ x² 2x be simplified if the terms are subtracted instead of multiplied?
A1: No. If the expression were x³ - x² - 2x, the simplification would be different. You cannot combine these terms because they are of different degrees. The simplification would remain as x³ - x² - 2x, which can be factored to some extent but not simplified further to a single term.
Q2: What happens if x is a negative number?
A2: If x is a negative number, the result of 2x⁶ will always be positive because an even power eliminates the negative sign. For instance, if x = -2, then 2x⁶ = 2(-2)⁶ = 2(64) = 128.
Q3: What are the roots of the equation 2x⁶ = 0?
A3: The only root (solution) for the equation 2x⁶ = 0 is x = 0. This is because the only value of x that makes the expression equal to zero is when x itself is zero.
Q4: How can I find the turning points of the graph of 2x⁶?
A4: Determining the turning points of the graph requires calculus. Specifically, you would need to find the first derivative of the function (12x⁵), set it equal to zero, and solve for x. The solutions will represent the x-coordinates of the turning points. Finding the second derivative will help determine if each turning point is a local minimum or maximum.
Conclusion
The seemingly simple mathematical expression x³ x² 2x reveals a wealth of mathematical principles and concepts. By understanding the rules of exponents and applying algebraic manipulation, we can simplify this expression to 2x⁶. This simplified form opens doors to analyzing its graphical representation, comprehending its behavior, and appreciating its widespread applications across diverse fields. Further exploration into expanding more complex expressions involving binomials highlights the versatility and power of algebraic methods in solving mathematical problems and modeling real-world phenomena. This article serves as a foundational guide for understanding the beauty and utility hidden within these mathematical constructs.
Latest Posts
Latest Posts
-
Words That Start With Jo
Sep 24, 2025
-
Gas Meter Display Not Working
Sep 24, 2025
-
Corbettmaths Area Of Compound Shapes
Sep 24, 2025
-
1 Square Feet To Cm
Sep 24, 2025
-
Photosynthesis As An Endothermic Reaction
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 2 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.