X 3 X 5 2
elan
Sep 15, 2025 · 5 min read
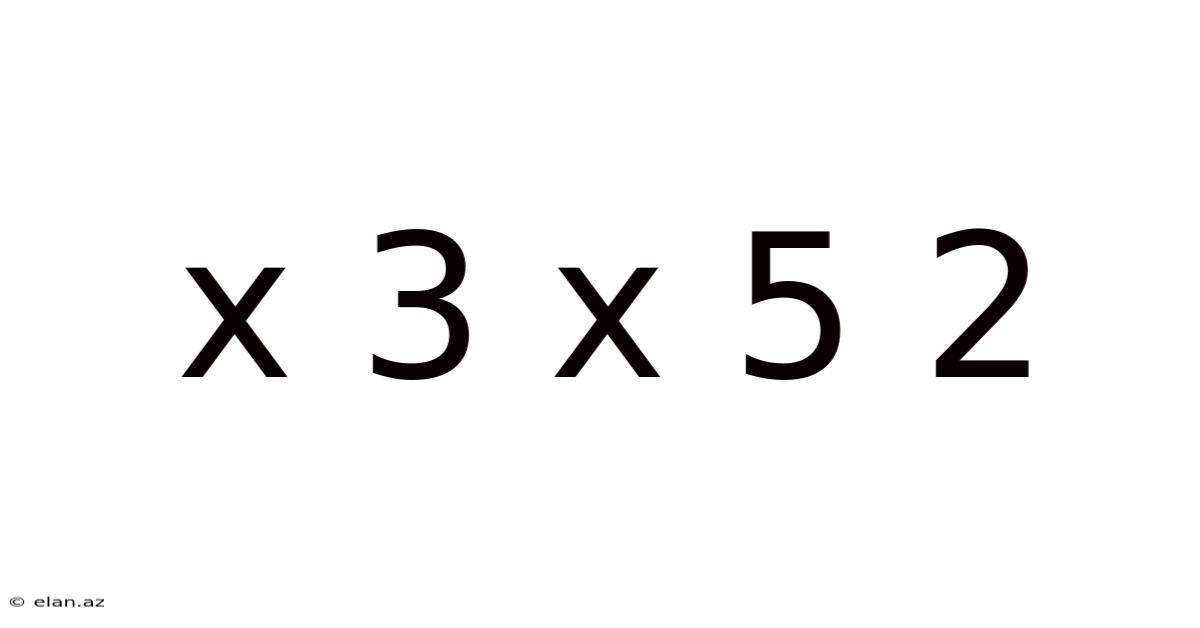
Table of Contents
Decoding the Enigma: A Deep Dive into "x 3 x 5 2"
The seemingly simple expression "x 3 x 5 2" presents a fascinating challenge, particularly when considering its potential interpretations and the underlying mathematical principles involved. This article will unravel the mystery behind this expression, exploring various possibilities, clarifying the order of operations (often remembered by the acronym PEMDAS/BODMAS), and illustrating the importance of precise mathematical notation. We'll examine scenarios where the expression might arise in real-world applications, and finally address potential misunderstandings and frequently asked questions.
Introduction: The Ambiguity of Mathematical Notation
At first glance, "x 3 x 5 2" appears straightforward. However, the lack of explicit parentheses or other grouping symbols introduces ambiguity. The order in which the operations (multiplication) are performed significantly impacts the final result. This ambiguity highlights the crucial role of precise mathematical notation in ensuring clarity and avoiding errors. Understanding the rules of precedence, specifically the order of operations, is paramount to correctly interpreting and solving this type of expression.
Understanding the Order of Operations (PEMDAS/BODMAS)
The order of operations, a fundamental concept in mathematics, dictates the sequence in which calculations should be performed within a mathematical expression. The acronyms PEMDAS and BODMAS are commonly used to remember the order:
- PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
- BODMAS: Brackets, Orders, Division and Multiplication (from left to right), Addition and Subtraction (from left to right).
Both acronyms represent the same order of operations; the only difference lies in the terminology used. "Parentheses" and "Brackets" are interchangeable, as are "Exponents" and "Orders."
Interpreting "x 3 x 5 2" Under Different Interpretations
Without parentheses, we must follow the order of operations strictly from left to right, treating multiplication as having equal precedence. Let's explore the possible interpretations:
Interpretation 1: Left-to-Right Evaluation
Following the left-to-right rule, we perform the operations sequentially:
- x 3: The variable 'x' is multiplied by 3, resulting in 3x.
- (3x) x 5: The result (3x) is then multiplied by 5, yielding 15x.
- (15x) 2: Finally, 15x is multiplied by 2, giving the final result of 30x.
Interpretation 2: Grouping with Implicit Parentheses (Unlikely but Possible)
Although less likely without explicit parentheses, one could hypothetically interpret the expression as implying groupings:
- (3 x 5): 3 is multiplied by 5, resulting in 15.
- x (15): The variable 'x' is multiplied by 15, resulting in 15x.
- (15x) 2: This is then multiplied by 2, resulting in 30x.
This interpretation, while yielding the same final result as the left-to-right approach in this specific example, underscores the importance of clear notation.
Interpretation 3: Introducing Parentheses for Clarity
The ambiguity is easily resolved by using parentheses to explicitly specify the intended order of operations. Different parenthesizations lead to different results:
- (x * 3) * (5 * 2): This evaluates to 30x, the same as the previous interpretations.
- x * (3 * 5) * 2: This also simplifies to 30x.
- x * (3 * (5 * 2)): This evaluates to 30x.
- (x * 3 * 5) * 2: This also simplifies to 30x.
However, consider this:
- x * (3 * 5 + 2): This evaluates to x * 17 = 17x.
- (x * 3) * 5 + 2: This evaluates to 15x + 2.
These examples clearly show how crucial the placement of parentheses is in defining the intended calculation.
Mathematical Context and Real-World Applications
Expressions similar to "x 3 x 5 2" can appear in various mathematical contexts. They often emerge in:
- Algebraic manipulations: When simplifying equations or solving for unknown variables, expressions with multiple multiplications are common.
- Geometric calculations: Area and volume calculations might involve multiplying several dimensions, leading to similar expressions.
- Programming and computer science: In programming, the order of operations is crucial for ensuring that calculations are performed correctly.
- Physics and engineering: Many formulas in physics and engineering involve multiple multiplications, where the order is strictly defined.
Addressing Potential Misunderstandings
A common misunderstanding arises from interpreting multiplication and division (or addition and subtraction) as having different precedences when they appear consecutively. Remember, they have equal precedence, and the order is determined by reading the expression from left to right.
Another common mistake is overlooking the significance of parentheses. They are not merely optional; they are essential for creating unambiguous mathematical expressions. The correct and consistent use of parentheses is paramount for effective communication in mathematics.
Frequently Asked Questions (FAQs)
Q1: Is there a universally accepted interpretation of "x 3 x 5 2" without parentheses?
A1: While the left-to-right evaluation based on the order of operations is the most widely accepted approach in the absence of parentheses, it remains crucial to use parentheses to avoid ambiguity and ensure clear communication.
Q2: Can this expression be simplified further?
A2: In the absence of a specific value for 'x', the expression simplifies to 30x. If a numerical value were assigned to 'x', the expression could then be further simplified to a single numerical value.
Q3: What if there were other operations involved, such as addition or subtraction?
A3: In that case, the order of operations (PEMDAS/BODMAS) would need to be strictly followed. Multiplication and division would be performed before addition and subtraction. The use of parentheses would remain vital for clarity.
Conclusion: The Power of Precision in Mathematical Notation
The seemingly simple expression "x 3 x 5 2" serves as a powerful reminder of the critical importance of precise mathematical notation. Ambiguity can lead to errors and misunderstandings. By understanding the order of operations and using parentheses effectively, we can ensure that mathematical expressions are clear, unambiguous, and correctly interpreted. This fundamental principle applies across all branches of mathematics and its applications in various fields of study and real-world problem-solving. The consistent application of these principles is essential for accurate and reliable calculations. Always prioritize clarity and precision in your mathematical work.
Latest Posts
Latest Posts
-
How To Calculate Entropy Change
Sep 15, 2025
-
The Shape Of Water Book
Sep 15, 2025
-
A Level Mathematics Formula Sheet
Sep 15, 2025
-
Formulae Booklet A Level Maths
Sep 15, 2025
-
Sine And Cosine Fourier Series
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 5 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.