2 15 As A Percentage
elan
Sep 13, 2025 · 6 min read
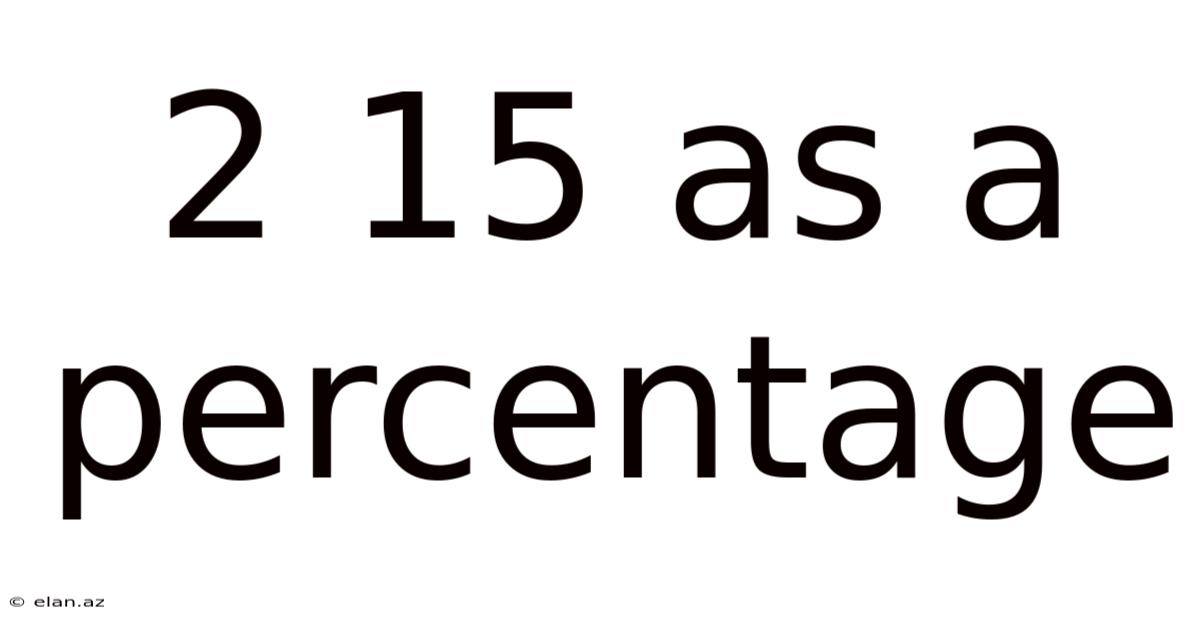
Table of Contents
Understanding 2/15 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This comprehensive guide will delve into the process of converting the fraction 2/15 into a percentage, explaining the method step-by-step and exploring various related concepts. We'll also address common misconceptions and provide practical examples to solidify your understanding. This will equip you with the knowledge to confidently handle similar fraction-to-percentage conversions in the future.
Introduction: Fractions, Decimals, and Percentages – A Unified Concept
Before we tackle 2/15 specifically, let's briefly review the interconnectedness of fractions, decimals, and percentages. They are all different ways of representing parts of a whole. A fraction expresses a part as a ratio of two numbers (numerator and denominator). A decimal represents a part as a number with a decimal point, signifying tenths, hundredths, thousandths, and so on. A percentage expresses a part as a fraction of 100, denoted by the symbol %.
Understanding this relationship is key. To convert a fraction to a percentage, we essentially find the equivalent fraction with a denominator of 100. This equivalent fraction can then be directly expressed as a percentage.
Method 1: Converting 2/15 to a Percentage using Decimal Conversion
This is perhaps the most straightforward approach. We first convert the fraction 2/15 into a decimal and then convert that decimal into a percentage.
-
Divide the numerator by the denominator: To convert the fraction 2/15 to a decimal, we divide the numerator (2) by the denominator (15):
2 ÷ 15 ≈ 0.1333...
Note that this results in a repeating decimal (0.1333...). We can round this to a certain number of decimal places depending on the required level of accuracy. For this example, we'll use four decimal places: 0.1333.
-
Multiply the decimal by 100: To convert the decimal to a percentage, we multiply it by 100:
0.1333 × 100 = 13.33%
Therefore, 2/15 is approximately 13.33%. The three dots (...) indicate that the decimal continues infinitely. The accuracy of the percentage depends on how many decimal places we consider in the initial decimal conversion.
Method 2: Converting 2/15 to a Percentage using Equivalent Fractions
This method involves finding an equivalent fraction with a denominator of 100. While not always directly achievable, it offers a valuable understanding of the underlying principle.
-
Find an equivalent fraction: We need to find a number that, when multiplied by 15, results in 100 or a close approximation. There isn't a whole number that perfectly achieves this. However, we can find a close approximation. Let's try to find a fraction that is approximately equal to 2/15 and has a denominator close to 100.
-
Approximate the equivalent fraction: To get closer to a denominator of 100, we can use a process of approximation. Since 15 * 6.666... ≈ 100, we can't use a whole number multiplier directly. However, we can understand that multiplying the numerator and denominator by 6.666... would get us reasonably close:
(2 * 6.666...) / (15 * 6.666...) ≈ 13.333... / 100
-
Express as a percentage: The approximate equivalent fraction is 13.333.../100, which directly translates to approximately 13.33%.
This method demonstrates the concept but may not be as practical as Method 1 for finding a precise result, especially for fractions that don't easily yield an equivalent fraction with a denominator of 100.
Method 3: Using a Calculator or Software
Most calculators and spreadsheet software (like Microsoft Excel or Google Sheets) have built-in functions for fraction-to-percentage conversion. Simply input the fraction 2/15 and the software will provide the percentage equivalent. This is the most efficient method for quick calculations.
Understanding the Significance of Repeating Decimals
The conversion of 2/15 yielded a repeating decimal (0.1333...). This is a common occurrence when converting fractions to decimals. A repeating decimal means the decimal part continues infinitely with a repeating pattern. When expressing this as a percentage, we often round the decimal to a certain number of decimal places for practical purposes. The level of rounding will depend on the context and the required accuracy. For most applications, rounding to two decimal places (13.33%) is sufficient. However, in some scientific or financial contexts, greater accuracy may be necessary.
Practical Applications of Percentage Conversions
Converting fractions to percentages is essential in various real-world scenarios:
- Discounts: A store offers a 2/15 discount on a product. Converting 2/15 to a percentage (13.33%) clarifies the discount amount.
- Tax calculations: Determining the sales tax on an item involves calculating a percentage of the price.
- Financial analysis: Understanding financial statements frequently requires converting fractions representing ratios or proportions into percentages for easier interpretation.
- Statistical analysis: Many statistical measures and representations utilize percentages.
- Grade calculations: Calculating a student’s final grade often involves averaging percentages representing different assessment components.
Frequently Asked Questions (FAQ)
-
Q: Why is the percentage an approximation?
- A: Because the decimal representation of 2/15 is a repeating decimal (0.1333...), we must round the decimal to a certain number of decimal places when expressing it as a percentage. This introduces a small degree of approximation.
-
Q: How many decimal places should I use when rounding?
- A: The number of decimal places depends on the context and required accuracy. Two decimal places (13.33%) are usually sufficient for most everyday applications. However, higher accuracy might be needed in specific situations.
-
Q: Can I use this method for other fractions?
- A: Yes, absolutely! The methods described above (division, equivalent fractions, and calculator use) can be applied to convert any fraction into a percentage.
-
Q: What if the fraction results in a non-repeating decimal?
- A: If the fraction results in a terminating decimal (a decimal that ends), the conversion to a percentage is exact, without any need for rounding.
-
Q: Is there a formula for converting fractions to percentages?
- A: Yes, the formula is: (Numerator / Denominator) * 100%. This formula encapsulates the steps we've outlined.
Conclusion: Mastering Fraction-to-Percentage Conversions
Understanding how to convert fractions to percentages is a vital mathematical skill. This guide has provided three distinct methods to accomplish this conversion for the fraction 2/15, highlighting the importance of understanding repeating decimals and the impact of rounding. By mastering these techniques, you'll gain confidence in handling percentage calculations across various applications in your daily life, studies, and professional endeavors. Remember that accuracy depends on the context, and understanding the underlying principles allows for informed decisions regarding the level of precision required in your calculations. Practice regularly, and you'll quickly become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
5 Letter Word Ending Ads
Sep 13, 2025
-
Main And Subordinate Clauses Examples
Sep 13, 2025
-
Lcm Of 12 15 10
Sep 13, 2025
-
Cng Pump Near By Me
Sep 13, 2025
-
Arrangement Of Flowers Crossword Clue
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2 15 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.