4 15 As A Percentage
elan
Sep 21, 2025 · 5 min read
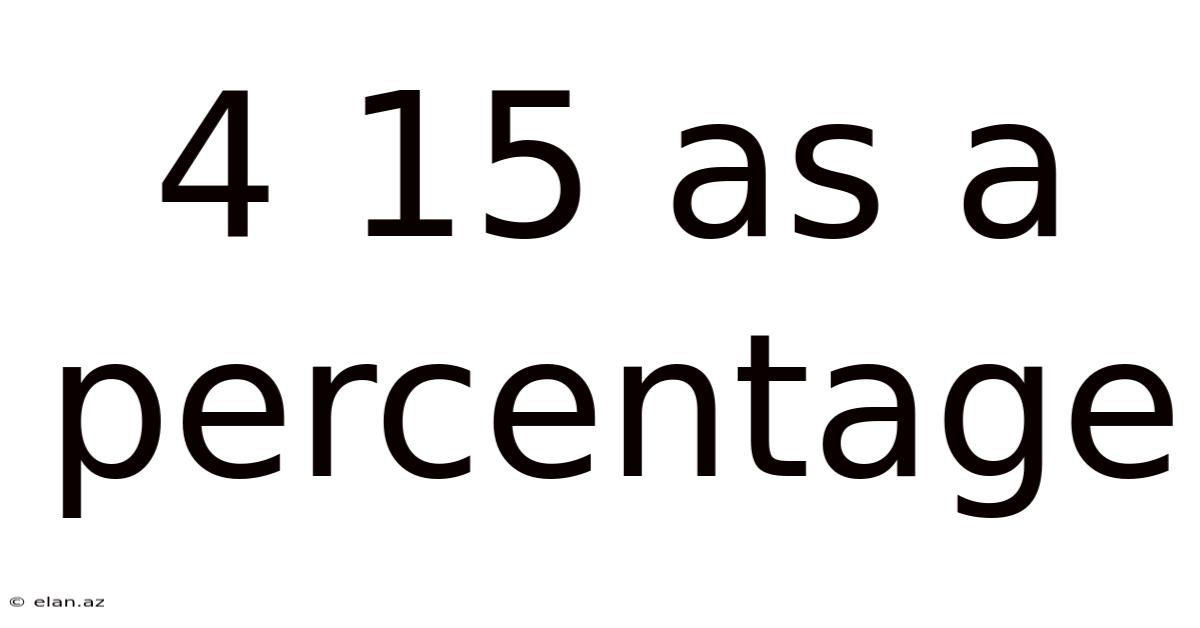
Table of Contents
Understanding 4/15 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in daily life, from calculating discounts and sales tax to understanding statistics and financial reports. This article provides a comprehensive guide to understanding how to convert the fraction 4/15 into a percentage, exploring various methods and delving into the underlying mathematical concepts. We'll also look at practical examples and address frequently asked questions to solidify your understanding.
Understanding Fractions and Percentages
Before we dive into converting 4/15 to a percentage, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. In our case, 4/15 means we have 4 parts out of a total of 15 equal parts.
A percentage, denoted by the symbol %, represents a fraction out of 100. It expresses a proportion as a fraction of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is arguably the most common and straightforward method. It involves two steps:
-
Convert the fraction to a decimal: To do this, divide the numerator (4) by the denominator (15).
4 ÷ 15 = 0.266666... (the 6 repeats infinitely – this is a recurring decimal)
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%).
0.266666... × 100 = 26.6666...%
Since the decimal is recurring, we can round it to a specific number of decimal places for practical purposes. Rounding to two decimal places, we get:
26.67%
Therefore, 4/15 is approximately equal to 26.67%. The "..." indicates that the decimal continues infinitely.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. This directly gives us the percentage because a percentage is a fraction out of 100. However, this method isn't always practical, especially with fractions that don't easily simplify to a denominator of 100.
To attempt this method, we would need to find a number that, when multiplied by 15, gives 100. Unfortunately, there's no whole number that satisfies this condition. This is because 100/15 is not a whole number. This illustrates why Method 1 is often preferred.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the percentage. We can set up a proportion:
4/15 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we can cross-multiply:
15x = 400
Then divide both sides by 15:
x = 400/15 = 26.6666...
This gives us the same result as Method 1: approximately 26.67%.
Practical Applications of Converting Fractions to Percentages
The ability to convert fractions to percentages is crucial in many real-world scenarios:
-
Calculating discounts: If a store offers a 4/15 discount on an item, you can convert 4/15 to a percentage (26.67%) to easily calculate the discount amount.
-
Understanding financial statements: Financial reports often use percentages to represent ratios and proportions. Converting fractions to percentages helps in interpreting these reports.
-
Analyzing test scores: If you answered 4 out of 15 questions correctly on a test, converting 4/15 to a percentage (26.67%) gives you your test score.
-
Calculating tax rates: Tax rates are often expressed as percentages. Understanding fraction-to-percentage conversion allows you to easily calculate the tax amount on a purchase.
-
Data analysis and statistics: In various fields, data is often represented as fractions or proportions. Converting these to percentages helps in easier interpretation and visualization.
The Significance of Recurring Decimals
The conversion of 4/15 results in a recurring decimal (0.2666...). This is common when converting fractions where the denominator has prime factors other than 2 and 5 (the prime factors of 10). Understanding recurring decimals is important for accurate calculations and appropriate rounding. In practical applications, rounding to a reasonable number of decimal places is usually sufficient.
Frequently Asked Questions (FAQs)
Q: Can I use a calculator to convert 4/15 to a percentage?
A: Yes, absolutely! Most calculators have a division function and can easily handle this conversion. Simply divide 4 by 15, then multiply the result by 100.
Q: Why is the percentage not a whole number?
A: The percentage isn't a whole number because the fraction 4/15 doesn't simplify to an equivalent fraction with a denominator of 100. Many fractions result in non-whole number percentages.
Q: What is the best method for converting fractions to percentages?
A: The most efficient and widely applicable method is converting the fraction to a decimal first, then multiplying by 100 to obtain the percentage.
Q: How do I round recurring decimals appropriately?
A: The appropriate number of decimal places depends on the context. For most practical purposes, rounding to two decimal places is sufficient. However, in some scientific or engineering applications, more decimal places may be necessary for accuracy.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with numerous real-world applications. While several methods exist, converting the fraction to a decimal first, then multiplying by 100, is generally the most straightforward and efficient approach. Understanding the concept of recurring decimals and appropriate rounding techniques is also crucial for obtaining accurate and practical results. Remember that 4/15 as a percentage is approximately 26.67%, a valuable piece of knowledge applicable across various disciplines. Mastering this conversion will significantly enhance your mathematical abilities and problem-solving skills in everyday situations.
Latest Posts
Latest Posts
-
7 11 As A Decimal
Sep 21, 2025
-
Wave Machine For Fish Tank
Sep 21, 2025
-
Diagram Of The Eye Gcse
Sep 21, 2025
-
Colors That Begin With U
Sep 21, 2025
-
Words To Describe A River
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 4 15 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.