7 11 As A Decimal
elan
Sep 21, 2025 · 5 min read
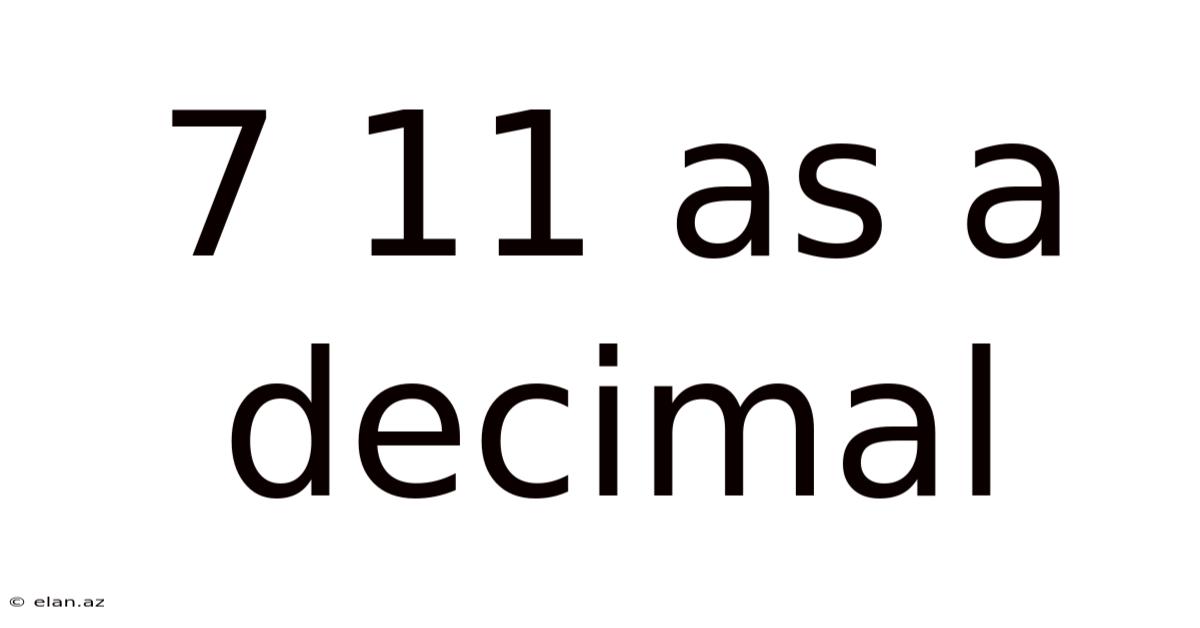
Table of Contents
7/11 as a Decimal: A Deep Dive into Fraction-to-Decimal Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This article will explore the conversion of the fraction 7/11 into its decimal equivalent, going beyond a simple answer to delve into the underlying principles and related concepts. We will cover various methods of conversion, address common misconceptions, and explore the unique characteristics of this specific fraction's decimal representation. By the end, you'll not only know the decimal value of 7/11 but also possess a deeper understanding of fractional and decimal systems.
Introduction: Fractions and Decimals – Two Sides of the Same Coin
Fractions and decimals are two different ways to represent the same concept: parts of a whole. A fraction expresses a part as a ratio of two integers (numerator and denominator), while a decimal uses base-10 notation, representing parts of a whole as tenths, hundredths, thousandths, and so on. Converting between fractions and decimals is essential for various mathematical operations and real-world applications. The fraction 7/11 presents a particularly interesting case study because its decimal representation showcases a recurring pattern.
Method 1: Long Division – The Classic Approach
The most straightforward method to convert a fraction to a decimal is through long division. To convert 7/11 to a decimal, we divide the numerator (7) by the denominator (11):
0.636363...
11 | 7.000000
-6.6
0.40
-33
0.70
-66
0.40
-33
0.70
-66
...
As you can see, the division process continues indefinitely, producing a repeating decimal. The digits "63" repeat endlessly. This is denoted by placing a bar over the repeating sequence: 0.6̅3̅.
Method 2: Understanding Repeating Decimals
The result of 7/11, 0.6̅3̅, is a repeating decimal, also known as a recurring decimal. This means the decimal representation has a sequence of digits that repeats infinitely. Not all fractions result in repeating decimals; some terminate (end after a finite number of digits), such as 1/4 (0.25). The nature of the decimal representation depends entirely on the denominator of the fraction in its simplest form. If the denominator contains prime factors other than 2 and 5, the decimal will repeat. Since 11 is a prime number different from 2 and 5, 7/11 produces a repeating decimal.
Method 3: Utilizing a Calculator
While long division provides a deeper understanding, a calculator offers a quick way to find the decimal equivalent. Simply divide 7 by 11 on your calculator. Depending on your calculator's display, you may see the decimal rounded off or a truncated version of the repeating sequence. However, the true value remains 0.6̅3̅.
The Significance of Repeating Decimals and Their Mathematical Properties
Repeating decimals have important mathematical properties. They can be expressed as fractions, demonstrating the inherent connection between fractions and decimals. Understanding repeating decimals is crucial in various mathematical fields, including:
- Calculus: Infinite series and limits often involve recurring decimals.
- Number Theory: The study of prime factorization and divisibility rules is closely linked to the behavior of fractions and their decimal representations.
- Algebra: Solving equations and inequalities can sometimes lead to solutions expressed as repeating decimals.
Common Misconceptions about Repeating Decimals
Several misconceptions surround repeating decimals:
- Rounding Error: It's crucial to understand that rounding a repeating decimal introduces an error. While 0.636363... is approximately 0.636, it's not precisely equal. The true value is the infinite repeating sequence.
- Termination: Students often mistakenly believe that a repeating decimal will eventually terminate. A true repeating decimal continues infinitely.
- Approximation vs. Exact Value: It's important to distinguish between an approximation (a rounded value) and the exact value (the infinite repeating decimal).
Exploring Similar Fractions and Patterns
Let's explore other fractions with a denominator of 11 to see if we can identify any patterns:
- 1/11 = 0.0̅9̅
- 2/11 = 0.1̅8̅
- 3/11 = 0.2̅7̅
- 4/11 = 0.3̅6̅
- 5/11 = 0.4̅5̅
- 6/11 = 0.5̅4̅
- 8/11 = 0.7̅2̅
- 9/11 = 0.8̅1̅
- 10/11 = 0.9̅0̅
Notice a pattern? The repeating digits always add up to 9. This isn't a coincidence, and exploring this further would lead into more advanced mathematical concepts related to modular arithmetic and number theory.
Converting Repeating Decimals Back to Fractions
It's also useful to know how to convert a repeating decimal back into a fraction. For 0.6̅3̅, we can use the following method:
- Let x = 0.636363...
- Multiply both sides by 100: 100x = 63.636363...
- Subtract the first equation from the second: 100x - x = 63.636363... - 0.636363... This simplifies to 99x = 63.
- Solve for x: x = 63/99.
- Simplify the fraction: Divide both numerator and denominator by 9 to get 7/11. This confirms our original fraction.
This method can be applied to any repeating decimal to find its fractional equivalent.
Frequently Asked Questions (FAQs)
Q: Is 0.63 an accurate representation of 7/11?
A: No, 0.63 is an approximation of 7/11. The true value is the infinitely repeating decimal 0.6̅3̅.
Q: Why does 7/11 have a repeating decimal?
A: Because the denominator (11) has prime factors other than 2 and 5.
Q: How can I quickly estimate the decimal value of 7/11?
A: You can use long division or a calculator for precision; however, a rough estimate can be obtained by noting it's slightly less than 0.7 (7/10).
Q: Are all fractions with a denominator of 11 repeating decimals?
A: Yes, all fractions with a denominator of 11 (in their simplest form) will produce a repeating decimal because 11 is a prime number other than 2 or 5.
Conclusion: Beyond the Simple Answer
This exploration of converting 7/11 into a decimal goes beyond a simple answer of 0.6̅3̅. We've delved into the underlying mathematical principles, explored different methods of conversion, addressed common misconceptions, and examined the unique characteristics of repeating decimals. Understanding these concepts provides a strong foundation for further mathematical exploration and problem-solving. Remember, the beauty of mathematics lies not just in the answers but in the journey of understanding the underlying processes. Mastering fraction-to-decimal conversion empowers you to tackle more complex mathematical challenges with confidence.
Latest Posts
Latest Posts
-
Solid Liquid And Gas Particles
Sep 21, 2025
-
Scientific Mistakes In The Quran
Sep 21, 2025
-
How To Sketch A Heart
Sep 21, 2025
-
Excel Convert Formula To Value
Sep 21, 2025
-
Green Vegetables List With Pictures
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 7 11 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.