6 20 As A Percent
elan
Sep 18, 2025 · 5 min read
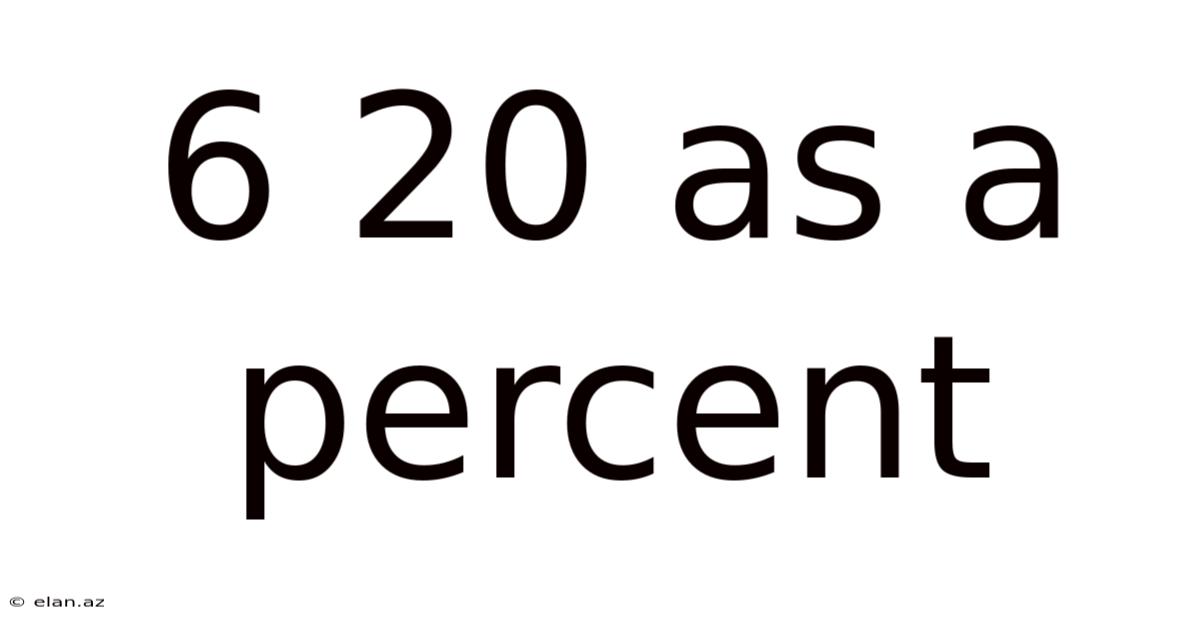
Table of Contents
6/20 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and sales tax to understanding statistical data and expressing proportions. This article provides a comprehensive guide to converting the fraction 6/20 into a percentage, exploring various methods and explaining the underlying principles. We'll delve into the steps involved, offer alternative approaches, and address frequently asked questions to ensure a thorough understanding of this crucial concept.
Introduction: Understanding Fractions and Percentages
Before diving into the specifics of converting 6/20, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts. A percentage, on the other hand, expresses a fraction as parts per hundred. The symbol "%" represents "per hundred" or "out of 100".
Method 1: Simplifying the Fraction and then Converting to Percentage
The most straightforward method involves simplifying the fraction 6/20 before converting it to a percentage. Simplification means reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
-
Find the Greatest Common Divisor (GCD): The GCD of 6 and 20 is 2.
-
Simplify the Fraction: Divide both the numerator and the denominator by the GCD: 6 ÷ 2 = 3 20 ÷ 2 = 10
This simplifies the fraction 6/20 to 3/10.
-
Convert the Simplified Fraction to a Percentage: To convert a fraction to a percentage, we multiply the fraction by 100%.
(3/10) * 100% = 30%
Therefore, 6/20 is equal to 30%.
Method 2: Direct Conversion from Fraction to Percentage
This method involves directly converting the fraction 6/20 to a percentage without simplification. While slightly more complex computationally, it demonstrates a more general approach applicable to any fraction.
-
Convert the Fraction to a Decimal: Divide the numerator by the denominator: 6 ÷ 20 = 0.3
-
Convert the Decimal to a Percentage: Multiply the decimal by 100%: 0.3 * 100% = 30%
Again, we arrive at the same result: 6/20 is equal to 30%.
Method 3: Using Proportions to Find the Percentage
This method utilizes the concept of proportions to solve the problem. We set up a proportion where the fraction 6/20 is equal to x/100, where 'x' represents the percentage we want to find.
-
Set up the Proportion: 6/20 = x/100
-
Cross-Multiply: 20x = 600
-
Solve for x: x = 600 ÷ 20 x = 30
Therefore, x = 30%, confirming that 6/20 is equal to 30%.
Understanding the Concept: Why does this work?
The reason these methods work stems from the definition of a percentage. A percentage is a fraction with a denominator of 100. By either simplifying the fraction or directly converting it to a decimal and then multiplying by 100, we are essentially finding the equivalent fraction with a denominator of 100. This equivalent fraction represents the percentage.
Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages has numerous real-world applications:
-
Calculating Discounts: If a store offers a 20% discount, and an item costs $50, you can calculate the discount by converting 20% to a fraction (20/100 = 1/5) and multiplying it by the price ($50 * 1/5 = $10).
-
Understanding Statistics: Statistical data often involves fractions and percentages. For example, understanding that 30% of survey respondents prefer a particular product provides valuable insights.
-
Financial Calculations: Interest rates, tax rates, and investment returns are commonly expressed as percentages. Converting fractions to percentages simplifies calculations and comparisons.
-
Expressing Proportions: Percentages are a concise way to represent proportions, making it easier to compare different ratios or parts of a whole.
Frequently Asked Questions (FAQs)
-
Q: What if the fraction is an improper fraction (numerator > denominator)? A: The process remains the same. Convert the improper fraction to a mixed number or decimal, and then proceed with the conversion to a percentage.
-
Q: What if the fraction involves decimals? A: Convert the decimal fraction to a regular fraction by multiplying both numerator and denominator by a power of 10 to eliminate the decimal. Then proceed with the usual conversion methods.
-
Q: Can I use a calculator for these conversions? A: Absolutely! Calculators are helpful for simplifying fractions and performing decimal calculations. However, understanding the underlying principles remains essential.
-
Q: Why is it important to learn these conversion methods? A: Mastering fraction-to-percentage conversion is crucial for various mathematical and real-world applications. It builds a strong foundation for more advanced mathematical concepts and improves your problem-solving skills.
-
Q: Are there any other methods to convert fractions to percentages? A: While the methods discussed are the most common and straightforward, more advanced techniques exist using proportions or algebraic manipulations, particularly useful when dealing with complex fractions or variables.
Conclusion: Mastering the Skill of Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill with wide-ranging applications. Understanding the various methods outlined in this article—simplification, direct conversion, and the use of proportions—provides you with a robust understanding of the process. By mastering this skill, you'll be better equipped to tackle various mathematical problems and confidently handle percentage-related calculations in your daily life. Remember that practice is key – the more you work with fractions and percentages, the more comfortable and proficient you will become. Don't hesitate to try different methods and choose the one that feels most intuitive to you. The most important thing is to understand the fundamental concept behind the conversion process. By applying these principles, you’ll confidently navigate the world of fractions and percentages.
Latest Posts
Latest Posts
-
Speed Distance And Time Graphs
Sep 18, 2025
-
Is Os A Scrabble Word
Sep 18, 2025
-
Words With Q In Middle
Sep 18, 2025
-
Lcm Of 105 And 130
Sep 18, 2025
-
5 3 Cm In Inches
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 6 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.