6 Divided By 2 5
elan
Sep 23, 2025 · 5 min read
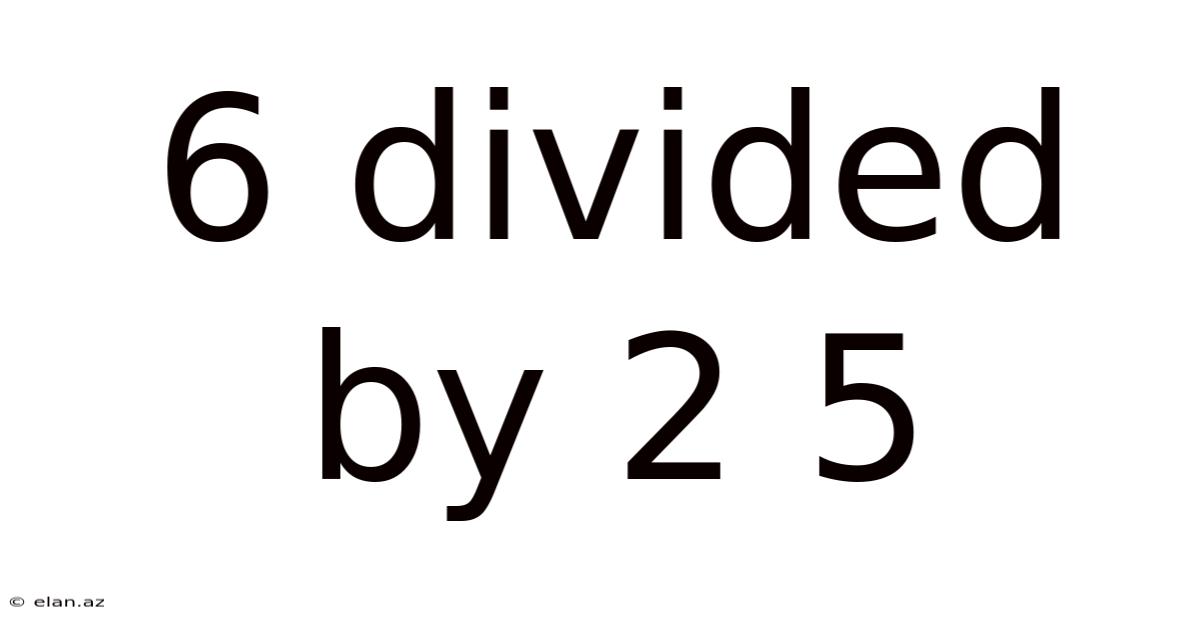
Table of Contents
Decoding 6 Divided by 2(5): Order of Operations and Mathematical Precision
The seemingly simple expression "6 divided by 2(5)" has sparked countless debates online, highlighting the crucial role of order of operations in mathematics. Understanding how to correctly solve this problem isn't just about getting the right answer; it's about grasping the fundamental rules that govern mathematical calculations and ensuring consistent results across different contexts. This article will delve into the solution, explaining the underlying principles of order of operations (PEMDAS/BODMAS), addressing common misconceptions, and exploring the importance of precise mathematical notation.
Understanding Order of Operations: PEMDAS/BODMAS
The correct order of operations is crucial for achieving a single, unambiguous answer to mathematical expressions. This is typically remembered using the acronyms PEMDAS or BODMAS:
- PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
- BODMAS: Brackets, Orders, Division and Multiplication (from left to right), Addition and Subtraction (from left to right).
Both acronyms represent the same fundamental principle: a hierarchical structure dictating the sequence of calculations. Let's break down each step:
-
Parentheses/Brackets: Calculations within parentheses (or brackets) must be performed first. This ensures that the innermost operations are resolved before proceeding outwards.
-
Exponents/Orders: Exponents (powers) or orders (roots and other higher-order operations) are evaluated next.
-
Multiplication and Division: These operations have equal precedence. If both appear in an expression, they are executed from left to right.
-
Addition and Subtraction: Similar to multiplication and division, addition and subtraction share equal precedence and are executed from left to right.
Solving 6 Divided by 2(5): A Step-by-Step Approach
Applying PEMDAS/BODMAS to "6 divided by 2(5)", we proceed as follows:
-
Implicit Multiplication: The expression "2(5)" represents implicit multiplication. There's an implied multiplication sign between the 2 and the 5. Many find this to be the source of confusion. It's crucial to recognize that this multiplication is not different from an explicitly written 2 x 5.
-
Parentheses/Brackets (Implicit): While there aren't explicit parentheses, the implied multiplication 2(5) acts as a grouping. Therefore, this operation takes precedence. We calculate 2 * 5 = 10. The expression now becomes 6 divided by 10.
-
Division: Finally, we perform the division: 6 / 10 = 0.6
Therefore, the correct answer to 6 divided by 2(5) is 0.6.
Addressing Common Misconceptions
Many arrive at the incorrect answer of 18 by incorrectly prioritizing multiplication over division. They solve the problem like this:
- Division First: They perform the division 6 / 2 = 3 first.
- Multiplication Next: Then they multiply by 5: 3 * 5 = 15. This order of operations is incorrect.
Another common mistake is treating the 2(5) as a completely separate entity, performing the division before addressing the implied multiplication. This highlights the importance of correctly identifying implicit multiplication and adhering strictly to the rules of PEMDAS/BODMAS.
The Importance of Precise Mathematical Notation
The ambiguity of the expression "6 divided by 2(5)" underscores the significance of precise mathematical notation. The lack of explicit division symbols can lead to misinterpretations. Using a fraction bar (/) or writing the expression as a fraction would eliminate any potential for confusion. For example:
- Fraction Notation: 6 / (2 * 5) clearly indicates the order of operations, leading to the correct answer of 0.6.
- Explicit Multiplication: 6 / (2 × 5) is another clearer way to present the equation.
Using clearer notation is essential to prevent any ambiguity and ensure that mathematical expressions are interpreted correctly. In more advanced mathematical contexts, precise notation becomes even more critical for avoiding errors.
Beyond the Basic Calculation: Exploring Related Concepts
While this specific problem highlights the importance of order of operations, it opens a door to exploring more advanced mathematical ideas.
-
Distributive Property: While not directly applicable to this specific problem, the distributive property is related. The distributive property states that a(b + c) = ab + ac. While we don't have addition or subtraction within the parentheses in this example, understanding the distributive property strengthens your foundation in algebra.
-
Algebraic Expressions: This problem demonstrates how important order of operations is when working with algebraic expressions. The principles remain the same whether dealing with numerical values or variables.
-
Computer Programming: Programming languages strictly adhere to order of operations to ensure consistent results. Understanding these principles is crucial for programmers to write accurate and reliable code.
Frequently Asked Questions (FAQ)
Q: Why isn't multiplication always performed before division?
A: Multiplication and division have the same precedence. They are performed from left to right. The same applies to addition and subtraction.
Q: Does the use of a calculator always provide the correct answer?
A: Most standard calculators will correctly evaluate the expression using PEMDAS/BODMAS if the expression is correctly entered. However, some simple calculators might not handle implicit multiplication correctly, leading to an incorrect answer.
Q: How can I avoid making mistakes with order of operations?
A: Practice! The more you work with these principles, the more comfortable and confident you will become. Use parentheses liberally to explicitly group operations.
Conclusion: Mastering the Fundamentals
The seemingly simple expression "6 divided by 2(5)" serves as a potent reminder of the critical role of order of operations in mathematics. By understanding and applying PEMDAS/BODMAS consistently, you can ensure accurate calculations and avoid the common pitfalls that lead to incorrect answers. Furthermore, emphasizing clear and precise mathematical notation helps prevent ambiguity and promotes consistent interpretation of mathematical expressions. Mastering these fundamentals is essential not just for solving simple problems but also for tackling more complex mathematical concepts in the future. Remember that precise mathematical language is as crucial as the mathematical concepts themselves. The ability to interpret and write mathematical statements clearly is a fundamental skill that will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
4 Crore Rupees In Pounds
Sep 23, 2025
-
5 7 As A Decimal
Sep 23, 2025
-
6 Divided By 3 5
Sep 23, 2025
-
Science Quiz Questions With Answers
Sep 23, 2025
-
What Does Rto Stand For
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 6 Divided By 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.