7 12 As A Percent
elan
Sep 20, 2025 · 5 min read
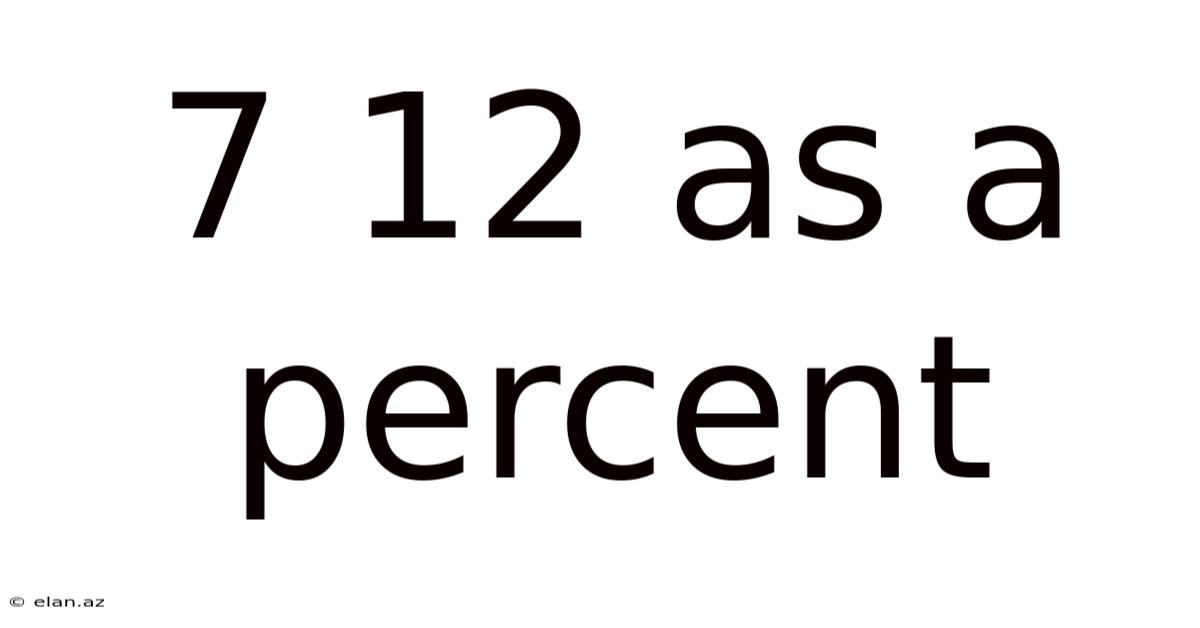
Table of Contents
Understanding 7/12 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the process of converting the fraction 7/12 into a percentage, exploring different methods, providing detailed explanations, and addressing common questions. Understanding this seemingly simple conversion will solidify your grasp of fractional representation and percentage calculations. This article will equip you with the knowledge and tools to confidently handle similar conversions in the future.
What is a Percentage?
Before we dive into converting 7/12, let's refresh our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" – it represents a portion out of a whole that is divided into 100 equal parts. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: Direct Conversion using Division
The most straightforward method for converting a fraction to a percentage is through division. We simply divide the numerator (the top number) by the denominator (the bottom number) and then multiply the result by 100%.
Let's apply this to 7/12:
-
Divide the numerator by the denominator: 7 ÷ 12 ≈ 0.583333...
-
Multiply the result by 100%: 0.583333... × 100% ≈ 58.33%
Therefore, 7/12 is approximately equal to 58.33%. Note that we use the approximation symbol (≈) because the decimal representation of 7/12 is a recurring decimal. We typically round the percentage to a convenient number of decimal places, depending on the context. In most cases, rounding to two decimal places (58.33%) provides sufficient accuracy.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction of 7/12 that has a denominator of 100. This method is particularly helpful when the denominator is a factor of 100 or can be easily manipulated to become one. While not directly applicable in this case (since 12 is not a factor of 100), understanding this method enhances our understanding of fractions and equivalent ratios.
To illustrate, let's consider a simpler example, such as 3/4. We can find an equivalent fraction with a denominator of 100 by multiplying both the numerator and the denominator by 25 (since 4 x 25 = 100):
(3 x 25) / (4 x 25) = 75/100 = 75%
For 7/12, finding a direct equivalent with a denominator of 100 is less intuitive. This highlights the advantage of the division method for fractions where finding an equivalent fraction with a denominator of 100 is not straightforward.
Method 3: Using a Calculator
Calculators are invaluable tools for these types of calculations. Most calculators have a percentage function that simplifies the process. Simply enter 7 ÷ 12 and then multiply the result by 100 to obtain the percentage. This method offers speed and accuracy, especially when dealing with complex fractions.
Understanding the Decimal Representation: 0.58333...
The decimal representation of 7/12, approximately 0.58333..., is important to understand. The recurring decimal '3' indicates that the decimal continues infinitely. This underscores the importance of rounding to a suitable number of decimal places for practical applications. This recurring decimal nature is a characteristic of many fractions when expressed as decimals, and understanding this will aid in comprehending percentage calculations involving fractions.
Practical Applications of 7/12 as a Percentage
Understanding that 7/12 is approximately 58.33% has various real-world applications. For example:
- Finance: Calculating interest rates, loan repayments, or profit margins.
- Statistics: Representing proportions or probabilities within datasets.
- Everyday Life: Determining discounts, calculating tips, or sharing portions of something.
Imagine you are sharing a pizza with 11 friends (12 people total). Your portion represents 7/12 of the pizza. Knowing that this is approximately 58.33% helps you quickly understand the size of your share compared to the whole.
Advanced Concepts: Accuracy and Significant Figures
The accuracy of the percentage calculation depends on the number of decimal places used. While 58.33% is a commonly used approximation, more decimal places could offer greater precision. However, the level of precision required depends entirely on the context of the problem. In scientific or engineering applications, higher precision might be necessary, while in everyday life, 58.33% usually suffices. The concept of significant figures is crucial when dealing with accuracy in numerical calculations.
Frequently Asked Questions (FAQ)
-
Q: Can 7/12 be expressed as an exact percentage?
A: No, 7/12 cannot be expressed as an exact percentage because its decimal representation is a recurring decimal. We can only approximate it to a certain number of decimal places.
-
Q: What are some other methods to convert fractions to percentages?
A: While division and finding equivalent fractions are common methods, some people prefer using proportions or cross-multiplication techniques. These methods, while effective, often involve more steps than simple division.
-
Q: How can I improve my understanding of fractions and percentages?
A: Practice is key! Work through various examples, try different conversion methods, and solve word problems that involve fractions and percentages. Online resources and educational materials can provide ample opportunities for practice.
-
Q: What is the difference between a fraction, a decimal, and a percentage?
A: They are all ways to represent parts of a whole. A fraction expresses a part as a ratio of two numbers (numerator/denominator). A decimal uses base-10 to represent parts of a whole. A percentage represents a part as a fraction of 100. They are all interchangeable and can be converted between each other.
Conclusion
Converting 7/12 to a percentage, yielding approximately 58.33%, is a fundamental skill that enhances your mathematical abilities. Understanding the different methods for conversion, including the importance of accuracy and rounding, provides a solid foundation for tackling more complex calculations involving fractions and percentages. Remember that the ability to effortlessly convert between fractions, decimals, and percentages is crucial in various academic and real-world scenarios. Mastering this concept will undoubtedly empower you to confidently approach similar challenges in the future. Continue practicing, and you will soon find these conversions second nature.
Latest Posts
Latest Posts
-
17 22 As A Percentage
Sep 20, 2025
-
Respiration Rate Of A Cat
Sep 20, 2025
-
Alphabet Tracing Worksheets A Z
Sep 20, 2025
-
X 2 2x 1 0
Sep 20, 2025
-
Animals That Start With F
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 7 12 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.