Lcm Of 12 15 18
elan
Sep 11, 2025 · 6 min read
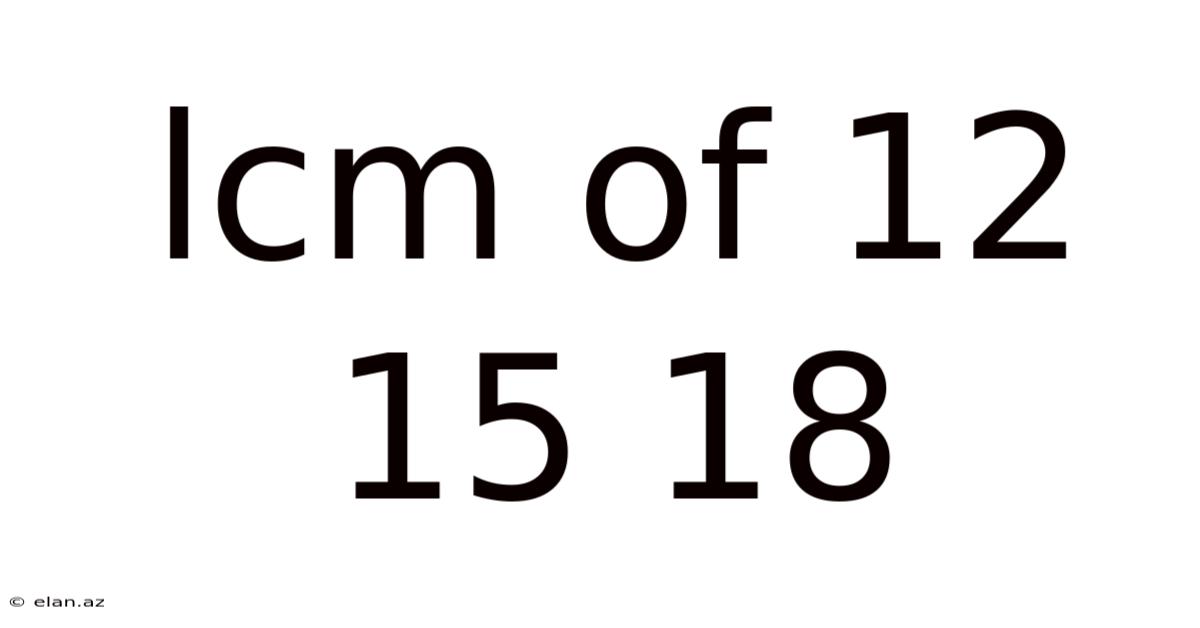
Table of Contents
Finding the Least Common Multiple (LCM) of 12, 15, and 18: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it provides a solid foundation in number theory and is crucial for various mathematical applications. This article will delve deep into finding the LCM of 12, 15, and 18, exploring multiple approaches, explaining the rationale behind each method, and addressing frequently asked questions. We'll go beyond just finding the answer and explore the why behind the calculations, making this a valuable resource for students and anyone interested in improving their mathematical understanding.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that all the given numbers can divide into evenly. This concept is fundamental in various mathematical contexts, including simplifying fractions, solving problems involving ratios and proportions, and even in more advanced areas like abstract algebra.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180...
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, 162, 180...
By comparing the lists, we can see that the smallest number that appears in all three lists is 180. Therefore, the LCM of 12, 15, and 18 is 180. While this method is simple for smaller numbers, it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method is more efficient and systematic, particularly for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Let's find the prime factorization of each number:
- 12 = 2² × 3
- 15 = 3 × 5
- 18 = 2 × 3²
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
Multiply these highest powers together: 4 × 9 × 5 = 180. Therefore, the LCM of 12, 15, and 18 is 180. This method is far more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of a set of numbers are closely related. There's a formula that connects them:
LCM(a, b, c) = (a × b × c) / GCD(a, b, c) (This formula can be extended to more than three numbers)
First, we need to find the GCD of 12, 15, and 18. We can use the Euclidean algorithm for this:
-
GCD(12, 15):
- 15 = 12 × 1 + 3
- 12 = 3 × 4 + 0
- The GCD(12, 15) is 3.
-
GCD(3, 18):
- 18 = 3 × 6 + 0
- The GCD(3, 18) is 3.
Therefore, the GCD(12, 15, 18) = 3.
Now, we can use the formula:
LCM(12, 15, 18) = (12 × 15 × 18) / 3 = 3240 / 3 = 180
This method is also efficient, especially if you already know how to calculate the GCD efficiently. The Euclidean algorithm is particularly useful for finding the GCD of larger numbers.
A Deeper Dive into Prime Factorization and its Importance
The prime factorization method is particularly powerful because it reveals the fundamental building blocks of the numbers. Prime numbers are the indivisible atoms of arithmetic; every other positive integer can be expressed as a unique product of prime numbers. Understanding prime factorization allows us to:
- Simplify fractions: By finding the prime factorization of the numerator and denominator, we can easily simplify fractions to their lowest terms.
- Solve problems involving ratios and proportions: Prime factorization helps in understanding the relationships between different quantities.
- Understand divisibility rules: Prime factorization provides insight into why certain divisibility rules work. For instance, a number is divisible by 3 if the sum of its digits is divisible by 3. This is directly related to the presence of the prime factor 3 in the number's prime factorization.
- Cryptography: Prime factorization plays a crucial role in modern cryptography, particularly in public-key cryptography systems like RSA. The difficulty of factoring large numbers into their prime factors is the basis of the security of these systems.
Applications of LCM in Real-World Scenarios
The concept of LCM extends beyond theoretical mathematics and finds practical applications in various real-world scenarios:
- Scheduling: Imagine three buses arrive at a bus stop at different intervals: one every 12 minutes, one every 15 minutes, and one every 18 minutes. The LCM (180 minutes) tells us when all three buses will arrive at the stop simultaneously.
- Construction: In construction projects, materials often come in different sizes or quantities. Determining the LCM can help optimize material usage and minimize waste.
- Music: The LCM is used in music theory to find the least common multiple of the lengths of different musical phrases or rhythms. This ensures that the musical piece concludes harmoniously.
- Manufacturing: Production lines often involve different processes or machines with varying cycle times. The LCM helps determine the most efficient scheduling of these processes.
Frequently Asked Questions (FAQ)
Q: What if the numbers have no common factors?
A: If the numbers are coprime (meaning they share no common factors other than 1), their LCM is simply the product of the numbers. For example, the LCM of 7 and 11 is 77 (7 x 11).
Q: Can I use a calculator to find the LCM?
A: Many scientific calculators have a built-in function to calculate the LCM. However, understanding the underlying methods is crucial for problem-solving and building a strong mathematical foundation.
Q: What is the difference between LCM and GCD?
A: The LCM is the smallest number that is a multiple of all the given numbers, while the GCD is the largest number that divides all the given numbers without leaving a remainder. They are inversely related, as shown in the formula LCM(a,b) = (a*b)/GCD(a,b).
Q: Can this method be extended to more than three numbers?
A: Yes, absolutely. Both the prime factorization method and the method using the GCD can be easily extended to find the LCM of any number of integers. For prime factorization, you simply consider all the prime factors from all the numbers and take the highest power of each. For the GCD method, you'll need to find the GCD of all the numbers first and then apply the extended version of the formula.
Conclusion
Finding the LCM of 12, 15, and 18, as we've demonstrated, is not just about arriving at the answer (180). It's about understanding the fundamental concepts of number theory, exploring different computational methods, and appreciating the practical applications of this seemingly simple arithmetic operation. Mastering these techniques equips you with valuable tools for tackling more complex mathematical problems and expands your understanding of the underlying principles that govern numbers. By understanding the why behind the calculations, you will not only be able to solve problems but also appreciate the elegance and power of mathematics.
Latest Posts
Latest Posts
-
Largest Cell In Human Body
Sep 11, 2025
-
Hcf Of 330 And 385
Sep 11, 2025
-
Convert 66 Inches To Cm
Sep 11, 2025
-
Advantages Of Building A Dam
Sep 11, 2025
-
Cube Numbers And Square Numbers
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 15 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.